1.4 柱坐标系与球坐标系简介 课件(25张PPT)
文档属性
| 名称 | 1.4 柱坐标系与球坐标系简介 课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 685.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-20 08:35:46 | ||
图片预览








文档简介
柱坐标系与球坐标系简介
1.了解在柱坐标系、球坐标系中刻画空间中点的位置的方法.
2.了解柱坐标、球坐标与直角坐标之间的变换公式.体会它们的区别.
1.球坐标系
建立空间直角坐标系O-xyz,设P是空间任意一点,连接OP,记|OP|=r,OP与Oz轴正向所夹的角为 ,P在Oxy平面上的射影为Q,Ox轴按逆时针方向旋转到OQ时所转过的最小正角为θ,点P的位置可以用有序数组(r, ,θ)表示,我们把建立上述对应关系的坐标系叫做球坐标系(或空间极坐标系).
有序数组(r, ,θ)叫做点P的球坐标,其中r≥0,0≤ ≤π,0≤θ<2π.
空间点P的直角坐标(x,y,z)与球坐标(r, ,θ)之间的变换关系为:
2.柱坐标系
建立空间直角坐标系O-xyz,设P是空间任意一点,在Oxy平面的射影为Q,用(ρ,θ)(ρ≥0,0≤θ<2π)表示点Q在平面Oxy上的极坐标,这时点P的位置可用有序数组(ρ,θ,z)(z∈R)表示.把建立上述对应关系的坐标系叫做柱坐标系.有序数组(ρ,θ,z)叫做点P的柱坐标,记作P(ρ,θ,z)其中ρ≥0,0≤θ<2π,z∈R.
点P的直角坐标(x,y,z)与柱坐标(ρ,θ,z)之间的变 换关系为:
练习
设点的球坐标为 ,它的直角坐标为____________.
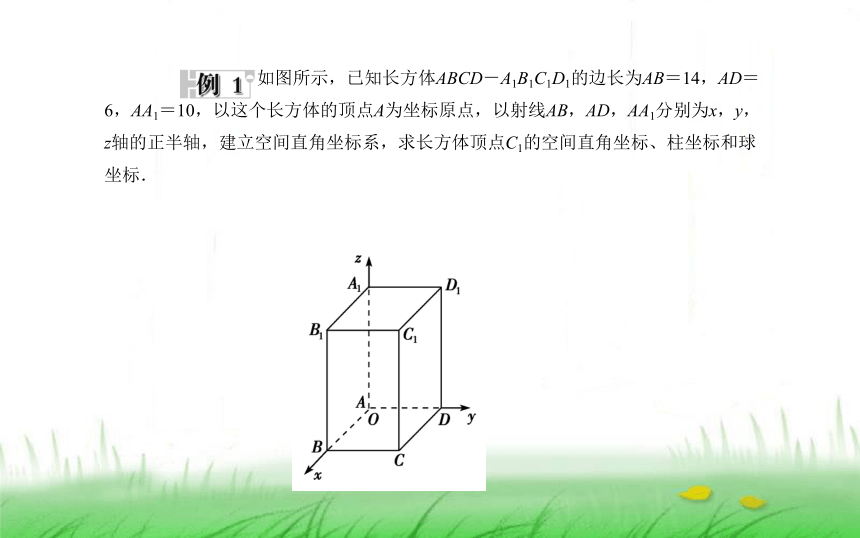
如图所示,已知长方体ABCD-A1B1C1D1的边长为AB=14,AD=6,AA1=10,以这个长方体的顶点A为坐标原点,以射线AB,AD,AA1分别为x,y,z轴的正半轴,建立空间直角坐标系,求长方体顶点C1的空间直角坐标、柱坐标和球坐标.
分析:本题考查空间直角坐标、柱坐标、球坐标的概念,我们要能借此区分三个坐标,找出它们的相同和不同来.
如图所示,点C1的(x,y,z)分别对应着CD,BC,CC1;点C1的(ρ,θ,z)分别对应着CA,∠BAC,CC1;点C1的(r,φ,θ)分别对应着AC1,∠A1AC1,∠BAC.
设点M的直角坐标为(1,1,3),求它的柱坐标.
分析:利用空间直角坐标与柱坐标的变换公式.
设点M的直角坐标为(1,1, ),求它的球坐标.
分析:利用球坐标公式求解.
C
B
3.已知点M的球坐标为 ,则它的直角坐标为________,它的柱坐标是______________.
4.设点M的柱坐标为 ,则它的直角坐标为________.
(-2,2,2 )
( ,1,7)
5.在球坐标系中,方程r=1表示________________,方程 = 表示空间的________________________.
6.在柱坐标系中,长方体ABCD-A1B1C1D1的一个顶点在原点,另两个顶点坐标分别为A1(8,0,10),C1 ,则此长方体外接球的体积为________.
5.球心在原点、半径为1的球面 顶点在原点、轴截面顶角为 的圆锥面
6.
B
10.一个圆形体育馆,自正东方向起,按逆时针方向等分为十六个扇形区域,顺次记为一区、二区……十六区.设圆形体育场第一排与体育中心的距离为200 m,每相邻两排的间距为1 m,每层看台的高度为0.7 m,现在需要确定第九区第四排正中的位置A,请建立适当的坐标系,求点A的坐标.求出来:
12.建立适当的柱坐标系,表示棱长为3的正四面体各个顶点坐标.
1.柱坐标系又称半极坐标系,它是由平面极坐标系及空间直角坐标系中的一部分建立起来的.
2.球坐标系在地理学、天文学中有着广泛应用,在测量实践中,球坐标中的角θ称为被测点P(r, ,θ)的方位角,90°- 称为高低角.
3.注意柱坐标P(ρ,θ,z)中各坐标分量的取值范围.ρ≥0,0≤θ<2π,-∞ 球坐标P(r, ,θ),其中r≥0,0≤ ≤π,0≤θ<2π.
4.柱坐标、球坐标与空间直角坐标的变换关系.
1.了解在柱坐标系、球坐标系中刻画空间中点的位置的方法.
2.了解柱坐标、球坐标与直角坐标之间的变换公式.体会它们的区别.
1.球坐标系
建立空间直角坐标系O-xyz,设P是空间任意一点,连接OP,记|OP|=r,OP与Oz轴正向所夹的角为 ,P在Oxy平面上的射影为Q,Ox轴按逆时针方向旋转到OQ时所转过的最小正角为θ,点P的位置可以用有序数组(r, ,θ)表示,我们把建立上述对应关系的坐标系叫做球坐标系(或空间极坐标系).
有序数组(r, ,θ)叫做点P的球坐标,其中r≥0,0≤ ≤π,0≤θ<2π.
空间点P的直角坐标(x,y,z)与球坐标(r, ,θ)之间的变换关系为:
2.柱坐标系
建立空间直角坐标系O-xyz,设P是空间任意一点,在Oxy平面的射影为Q,用(ρ,θ)(ρ≥0,0≤θ<2π)表示点Q在平面Oxy上的极坐标,这时点P的位置可用有序数组(ρ,θ,z)(z∈R)表示.把建立上述对应关系的坐标系叫做柱坐标系.有序数组(ρ,θ,z)叫做点P的柱坐标,记作P(ρ,θ,z)其中ρ≥0,0≤θ<2π,z∈R.
点P的直角坐标(x,y,z)与柱坐标(ρ,θ,z)之间的变 换关系为:
练习
设点的球坐标为 ,它的直角坐标为____________.
如图所示,已知长方体ABCD-A1B1C1D1的边长为AB=14,AD=6,AA1=10,以这个长方体的顶点A为坐标原点,以射线AB,AD,AA1分别为x,y,z轴的正半轴,建立空间直角坐标系,求长方体顶点C1的空间直角坐标、柱坐标和球坐标.
分析:本题考查空间直角坐标、柱坐标、球坐标的概念,我们要能借此区分三个坐标,找出它们的相同和不同来.
如图所示,点C1的(x,y,z)分别对应着CD,BC,CC1;点C1的(ρ,θ,z)分别对应着CA,∠BAC,CC1;点C1的(r,φ,θ)分别对应着AC1,∠A1AC1,∠BAC.
设点M的直角坐标为(1,1,3),求它的柱坐标.
分析:利用空间直角坐标与柱坐标的变换公式.
设点M的直角坐标为(1,1, ),求它的球坐标.
分析:利用球坐标公式求解.
C
B
3.已知点M的球坐标为 ,则它的直角坐标为________,它的柱坐标是______________.
4.设点M的柱坐标为 ,则它的直角坐标为________.
(-2,2,2 )
( ,1,7)
5.在球坐标系中,方程r=1表示________________,方程 = 表示空间的________________________.
6.在柱坐标系中,长方体ABCD-A1B1C1D1的一个顶点在原点,另两个顶点坐标分别为A1(8,0,10),C1 ,则此长方体外接球的体积为________.
5.球心在原点、半径为1的球面 顶点在原点、轴截面顶角为 的圆锥面
6.
B
10.一个圆形体育馆,自正东方向起,按逆时针方向等分为十六个扇形区域,顺次记为一区、二区……十六区.设圆形体育场第一排与体育中心的距离为200 m,每相邻两排的间距为1 m,每层看台的高度为0.7 m,现在需要确定第九区第四排正中的位置A,请建立适当的坐标系,求点A的坐标.求出来:
12.建立适当的柱坐标系,表示棱长为3的正四面体各个顶点坐标.
1.柱坐标系又称半极坐标系,它是由平面极坐标系及空间直角坐标系中的一部分建立起来的.
2.球坐标系在地理学、天文学中有着广泛应用,在测量实践中,球坐标中的角θ称为被测点P(r, ,θ)的方位角,90°- 称为高低角.
3.注意柱坐标P(ρ,θ,z)中各坐标分量的取值范围.ρ≥0,0≤θ<2π,-∞
4.柱坐标、球坐标与空间直角坐标的变换关系.
