2.1 曲线的参数方程 课件(22张PPT)
文档属性
| 名称 | 2.1 曲线的参数方程 课件(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 192.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-20 08:38:34 | ||
图片预览







文档简介
曲线的参数方程
1、参数方程的概念:
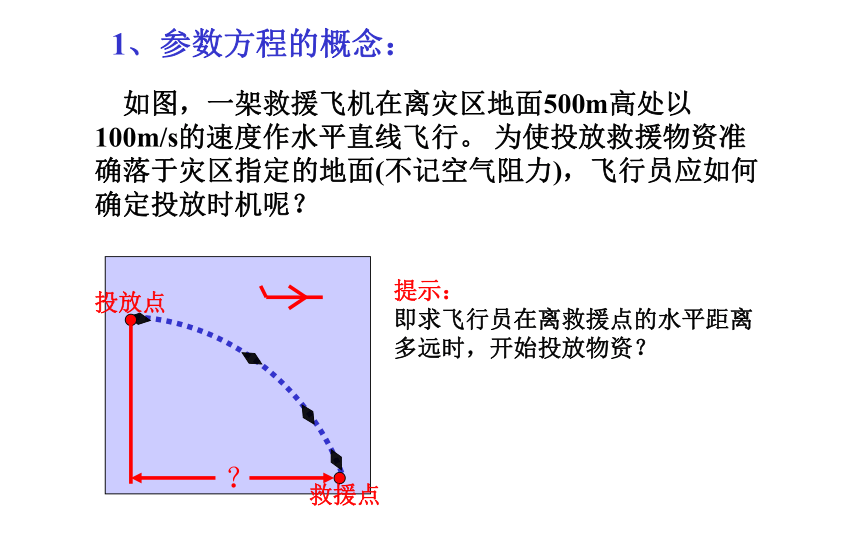
如图,一架救援飞机在离灾区地面500m高处以100m/s的速度作水平直线飞行。 为使投放救援物资准确落于灾区指定的地面(不记空气阻力),飞行员应如何确定投放时机呢?
提示:
即求飞行员在离救援点的水平距离
多远时,开始投放物资?
?
救援点
投放点
1、参数方程的概念:
x
y
500
o
物资投出机舱后,它的运动由下列两种运动合成:
(1)沿ox作初速为100m/s的匀速直线运动;
(2)沿oy反方向作自由落体运动。
如图,一架救援飞机在离灾区地面500m高处以100m/s的速度作水平直线飞行。为使投放救援物资准确落于灾区指定的地面(不记空气阻力),飞行员应如何确定投放时机呢?
x
y
500
o
1、参数方程的概念:
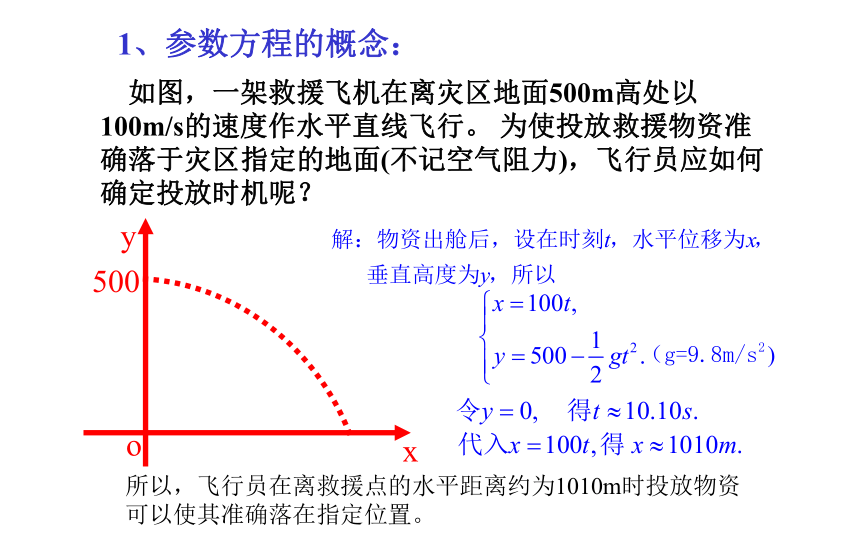
如图,一架救援飞机在离灾区地面500m高处以100m/s的速度作水平直线飞行。 为使投放救援物资准确落于灾区指定的地面(不记空气阻力),飞行员应如何确定投放时机呢?
所以,飞行员在离救援点的水平距离约为1010m时投放物资可以使其准确落在指定位置。
一、方程组有3个变量,其中的x,y表示点的坐标,变量t叫做参变量,而且x,y分别是t的函数。
二、由物理知识可知,物体的位置由时间t唯一决定,从数学角度看,这就是点M的坐标x,y由t唯一确定,这样当t在允许值范围内连续变化时,x,y的值也随之连续地变化,于是就可以连续地描绘出点的轨迹。
三、平抛物体运动轨迹上的点与满足方程组的有序实数对(x,y)之间有一一对应关系。
并且对于t的每一个允许值, 由方程组,所确定的点M(x,y)都在这条曲线上, 那么方程, 就叫做这条曲线的参数方程, 联系变数x,y的变数t叫做参变数, 简称参数。
相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程。
关于参数几点说明: 参数是联系变数x,y的桥梁,
1.参数方程中参数可以是有物理意义,几何意义,也可以没有明显意义。
2.同一曲线选取参数不同,曲线参数方程形式也不一样。
3.在实际问题中要确定参数的取值范围。
1、参数方程的概念:
一般地, 在平面直角坐标系中,如果曲线上任意一点的坐标x, y都是某个变数t的函数
例1: 已知曲线C的参数方程是
(1)判断点M1(0, 1),M2(5, 4)与曲线C的位置关系;
(2)已知点M3(6, a)在曲线C上,求a的值。
一架救援飞机以100m/s的速度作水平直线飞行.在离灾区指定目标1000m时投放救援物资(不计空气阻力,重力加速 g=10m/s)问此时飞机的飞行高度约是多少?(精确到1m)
变式:
2、方程 所表示的曲线上一点的坐标是
( )
练习1
A、(2,7);B、 C、 D、(1,0)
1、曲线 与x轴的交点坐标是( )
A、(1,4);B、 C、 D、
B
D
已知曲线C的参数方程是
点M(5,4)在该 曲线上.
(1)求常数a;
(2)求曲线C的普通方程。
解:
(1)由题意可知:
1+2t=5
at2=4
解得:
a=1
t=2
∴ a=1
(2)由已知及(1)可得,曲线C的方程为:
x=1+2t
y=t2
由第一个方程得:
代入第二个方程得:
练习2:
思考题:动点M作等速直线运动, 它在x轴和y轴方向的速度分别为5和12 , 运动开始时位于点P(1,2), 求点M的轨迹参数方程。
解:设动点M (x,y) 运动时间为t,依题意,得
所以,点M的轨迹参数方程为
参数方程求法:
(1)建立直角坐标系, 设曲线上任一点P坐标为(x,y)
(2)选取适当的参数
(3)根据已知条件和图形的几何性质, 物理意义,
建立点P坐标与参数的函数式
(4)证明这个参数方程就是所由于的曲线的方程
小结:
一般地,在平面直角坐标系中,如果曲线上任意一点的坐标
x,y都是某个变数t的函数
(2)
并且对于t的每一个允许值,由方程组(2)所确定的点M(x,y)都在这条曲线上,
那么方程(2)就叫做这条曲线的参数方程,
系变数x,y的变数t叫做参变数,简称参数。
2、圆的参数方程
y
x
o
r
M(x,y)
圆的参数方程的一般形式
由于选取的参数不同,圆有不同的参数方程,一般地,同一条曲线,可以选取不同的变数为参数,因此得到的参数方程也可以有不同的形式,形式不同的参数方程,它们表示 的曲线可以是相同的,另外,在建立曲线的参数时,要注明参数及参数的取值范围。
例1、已知圆方程x2+y2 +2x-6y+9=0,将它化为参数方程。
解: x2+y2+2x-6y+9=0化为标准方程,
(x+1)2+(y-3)2=1,
∴参数方程为
(θ为参数)
例2 如图,圆O的半径为2,P是圆上的动点,Q(6,0)是x轴上的定点,M是PQ的中点,当点P绕O作匀速圆周运动时,求点M的轨迹的参数方程。
y
o
x
P
M
Q
(2,1)
1、参数方程的概念:
如图,一架救援飞机在离灾区地面500m高处以100m/s的速度作水平直线飞行。 为使投放救援物资准确落于灾区指定的地面(不记空气阻力),飞行员应如何确定投放时机呢?
提示:
即求飞行员在离救援点的水平距离
多远时,开始投放物资?
?
救援点
投放点
1、参数方程的概念:
x
y
500
o
物资投出机舱后,它的运动由下列两种运动合成:
(1)沿ox作初速为100m/s的匀速直线运动;
(2)沿oy反方向作自由落体运动。
如图,一架救援飞机在离灾区地面500m高处以100m/s的速度作水平直线飞行。为使投放救援物资准确落于灾区指定的地面(不记空气阻力),飞行员应如何确定投放时机呢?
x
y
500
o
1、参数方程的概念:
如图,一架救援飞机在离灾区地面500m高处以100m/s的速度作水平直线飞行。 为使投放救援物资准确落于灾区指定的地面(不记空气阻力),飞行员应如何确定投放时机呢?
所以,飞行员在离救援点的水平距离约为1010m时投放物资可以使其准确落在指定位置。
一、方程组有3个变量,其中的x,y表示点的坐标,变量t叫做参变量,而且x,y分别是t的函数。
二、由物理知识可知,物体的位置由时间t唯一决定,从数学角度看,这就是点M的坐标x,y由t唯一确定,这样当t在允许值范围内连续变化时,x,y的值也随之连续地变化,于是就可以连续地描绘出点的轨迹。
三、平抛物体运动轨迹上的点与满足方程组的有序实数对(x,y)之间有一一对应关系。
并且对于t的每一个允许值, 由方程组,所确定的点M(x,y)都在这条曲线上, 那么方程, 就叫做这条曲线的参数方程, 联系变数x,y的变数t叫做参变数, 简称参数。
相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程。
关于参数几点说明: 参数是联系变数x,y的桥梁,
1.参数方程中参数可以是有物理意义,几何意义,也可以没有明显意义。
2.同一曲线选取参数不同,曲线参数方程形式也不一样。
3.在实际问题中要确定参数的取值范围。
1、参数方程的概念:
一般地, 在平面直角坐标系中,如果曲线上任意一点的坐标x, y都是某个变数t的函数
例1: 已知曲线C的参数方程是
(1)判断点M1(0, 1),M2(5, 4)与曲线C的位置关系;
(2)已知点M3(6, a)在曲线C上,求a的值。
一架救援飞机以100m/s的速度作水平直线飞行.在离灾区指定目标1000m时投放救援物资(不计空气阻力,重力加速 g=10m/s)问此时飞机的飞行高度约是多少?(精确到1m)
变式:
2、方程 所表示的曲线上一点的坐标是
( )
练习1
A、(2,7);B、 C、 D、(1,0)
1、曲线 与x轴的交点坐标是( )
A、(1,4);B、 C、 D、
B
D
已知曲线C的参数方程是
点M(5,4)在该 曲线上.
(1)求常数a;
(2)求曲线C的普通方程。
解:
(1)由题意可知:
1+2t=5
at2=4
解得:
a=1
t=2
∴ a=1
(2)由已知及(1)可得,曲线C的方程为:
x=1+2t
y=t2
由第一个方程得:
代入第二个方程得:
练习2:
思考题:动点M作等速直线运动, 它在x轴和y轴方向的速度分别为5和12 , 运动开始时位于点P(1,2), 求点M的轨迹参数方程。
解:设动点M (x,y) 运动时间为t,依题意,得
所以,点M的轨迹参数方程为
参数方程求法:
(1)建立直角坐标系, 设曲线上任一点P坐标为(x,y)
(2)选取适当的参数
(3)根据已知条件和图形的几何性质, 物理意义,
建立点P坐标与参数的函数式
(4)证明这个参数方程就是所由于的曲线的方程
小结:
一般地,在平面直角坐标系中,如果曲线上任意一点的坐标
x,y都是某个变数t的函数
(2)
并且对于t的每一个允许值,由方程组(2)所确定的点M(x,y)都在这条曲线上,
那么方程(2)就叫做这条曲线的参数方程,
系变数x,y的变数t叫做参变数,简称参数。
2、圆的参数方程
y
x
o
r
M(x,y)
圆的参数方程的一般形式
由于选取的参数不同,圆有不同的参数方程,一般地,同一条曲线,可以选取不同的变数为参数,因此得到的参数方程也可以有不同的形式,形式不同的参数方程,它们表示 的曲线可以是相同的,另外,在建立曲线的参数时,要注明参数及参数的取值范围。
例1、已知圆方程x2+y2 +2x-6y+9=0,将它化为参数方程。
解: x2+y2+2x-6y+9=0化为标准方程,
(x+1)2+(y-3)2=1,
∴参数方程为
(θ为参数)
例2 如图,圆O的半径为2,P是圆上的动点,Q(6,0)是x轴上的定点,M是PQ的中点,当点P绕O作匀速圆周运动时,求点M的轨迹的参数方程。
y
o
x
P
M
Q
(2,1)
