2.3 直线的参数方程 课件(24张PPT)
文档属性
| 名称 | 2.3 直线的参数方程 课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 500.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-20 00:00:00 | ||
图片预览






文档简介
直线的参数方程
请同学们回忆:
我们学过的直线的普通方程都有哪些?
两点式:
点斜式:
一般式:
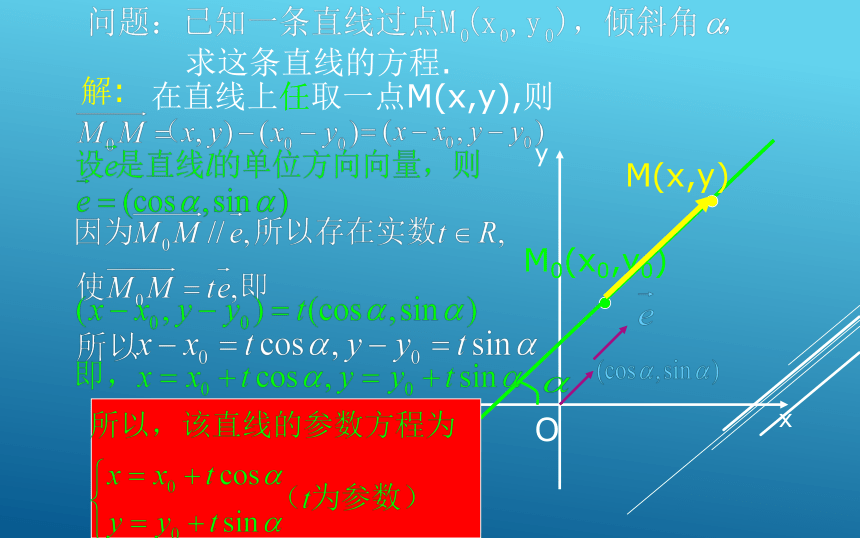
求这条直线的方程.
解:
要注意:
, 都是常数,t才是参数
求这条直线的方程.
M0(x0,y0)
M(x,y)
x
O
y
解:
在直线上任取一点M(x,y),则
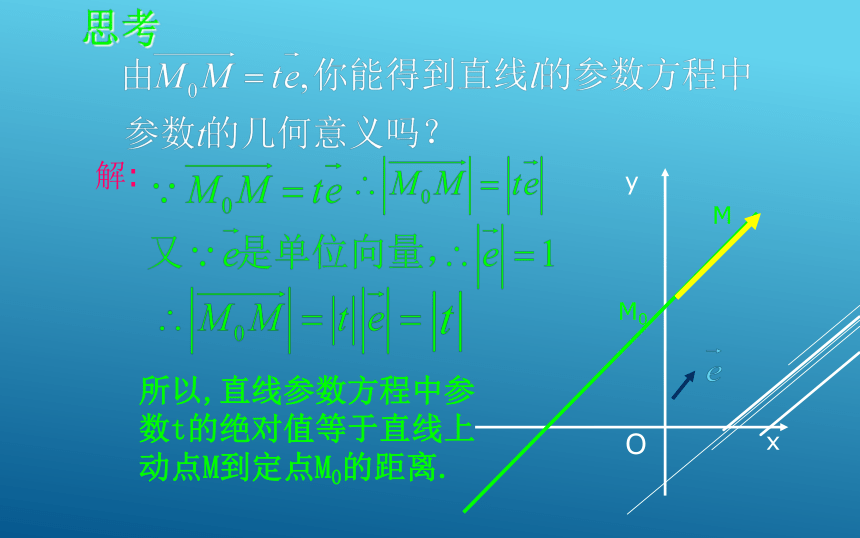
思考
x
y
O
M0
M
解:
所以,直线参数方程中参数t的绝对值等于直线上动点M到定点M0的距离.
这就是t的几何意义,要牢记
|t|=|M0M|
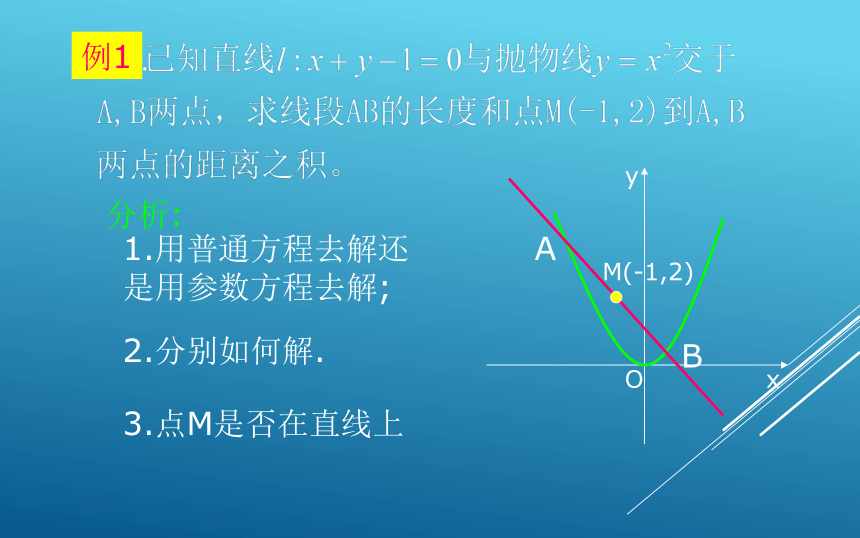
分析:
3.点M是否在直线上
1.用普通方程去解还是用参数方程去解;
2.分别如何解.
例1
A
B
M(-1,2)
x
y
O
例1
A
B
M(-1,2)
x
y
O
解:
因为把点M的坐标代入直线方程后,符合直线方程,所以点M在直线上.
易知直线的倾斜角为
把它代入抛物线y=x2的方程,得
A
B
M(-1,2)
x
y
O
探究
练习
练习
小结:
1.直线参数方程
探究:直线的参数方程形式是不是唯一的
3.注意向量工具的使用.
|t|=|M0M|
2.利用直线参数方程中参数t的几何意义,简化求直线上两点间的距离.
5.动点M作匀速直线运动,它在x轴和y轴方向的分速度分别是3m/s和4m/s,直角坐标系的长度单位是1cm,点M的起始位置在点M0(2,1)处,求点M的轨迹的参数方程.
分析:
我们是否可以根据t的值来确定向量
的方向呢?
此时,若t>0,则
的方向向上;
若t<0,则
的点方向向下;
若t=0,则M与点
M0重合.
辨析:
例:动点M作等速直线运动,它在x轴和y轴方向分速度分别为9,12,运动开始时,点M位于A(1,1),求点M的轨迹的参数方程.
解:
请思考:此时的t有没有明确的几何意义?
没有
重要结论:
直线的参数方程可以写成这样的形式:
请同学们回忆:
我们学过的直线的普通方程都有哪些?
两点式:
点斜式:
一般式:
求这条直线的方程.
解:
要注意:
, 都是常数,t才是参数
求这条直线的方程.
M0(x0,y0)
M(x,y)
x
O
y
解:
在直线上任取一点M(x,y),则
思考
x
y
O
M0
M
解:
所以,直线参数方程中参数t的绝对值等于直线上动点M到定点M0的距离.
这就是t的几何意义,要牢记
|t|=|M0M|
分析:
3.点M是否在直线上
1.用普通方程去解还是用参数方程去解;
2.分别如何解.
例1
A
B
M(-1,2)
x
y
O
例1
A
B
M(-1,2)
x
y
O
解:
因为把点M的坐标代入直线方程后,符合直线方程,所以点M在直线上.
易知直线的倾斜角为
把它代入抛物线y=x2的方程,得
A
B
M(-1,2)
x
y
O
探究
练习
练习
小结:
1.直线参数方程
探究:直线的参数方程形式是不是唯一的
3.注意向量工具的使用.
|t|=|M0M|
2.利用直线参数方程中参数t的几何意义,简化求直线上两点间的距离.
5.动点M作匀速直线运动,它在x轴和y轴方向的分速度分别是3m/s和4m/s,直角坐标系的长度单位是1cm,点M的起始位置在点M0(2,1)处,求点M的轨迹的参数方程.
分析:
我们是否可以根据t的值来确定向量
的方向呢?
此时,若t>0,则
的方向向上;
若t<0,则
的点方向向下;
若t=0,则M与点
M0重合.
辨析:
例:动点M作等速直线运动,它在x轴和y轴方向分速度分别为9,12,运动开始时,点M位于A(1,1),求点M的轨迹的参数方程.
解:
请思考:此时的t有没有明确的几何意义?
没有
重要结论:
直线的参数方程可以写成这样的形式:
