(湘教版)2018-2019学年高中数学第三章三角函数3.2任意角的三角函数3.2.3诱导公式(一)课件必修2(31张PPT)
文档属性
| 名称 | (湘教版)2018-2019学年高中数学第三章三角函数3.2任意角的三角函数3.2.3诱导公式(一)课件必修2(31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 874.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-20 08:00:04 | ||
图片预览






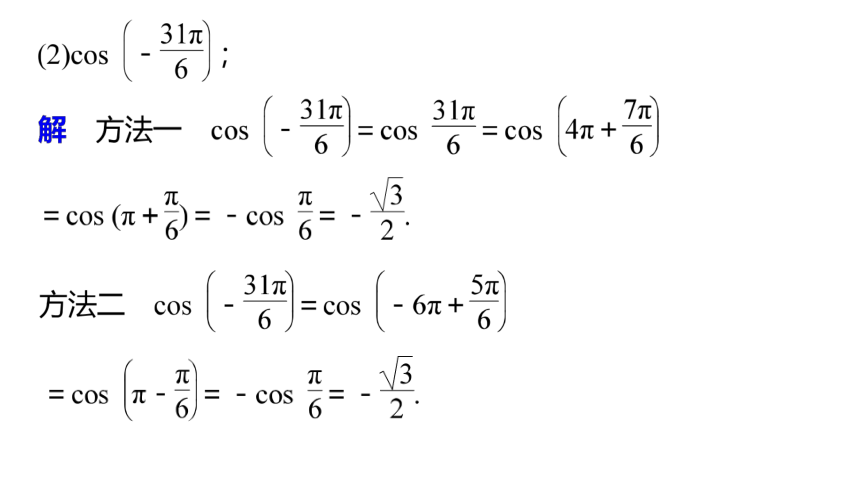
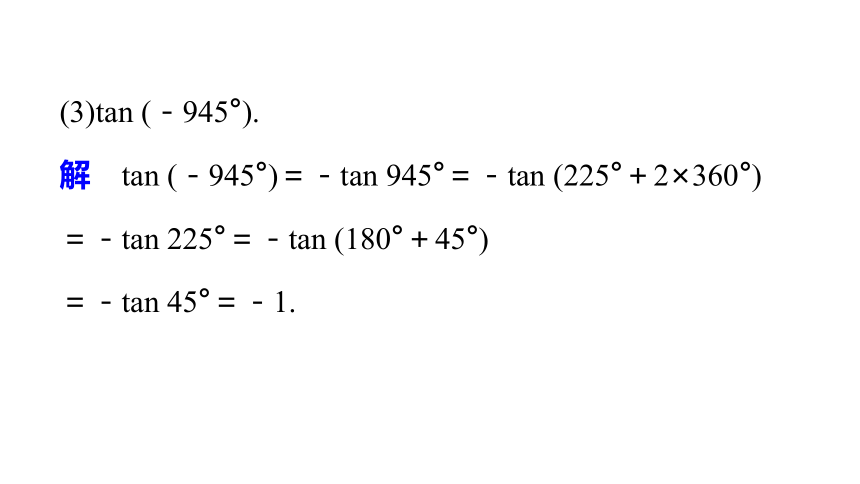


文档简介
课件31张PPT。第3章——三角函数3.2 任意角的三角函数
3.2.3 诱导公式(一)[学习目标]1.了解三角函数的诱导公式的意义和作用.
2.理解诱导公式的推导过程.
3.能运用有关诱导公式解决一些三角函数的求值、化简和证明问题.1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功1.对于任意一个角α,与它终边相同的角的集合应如何表示?
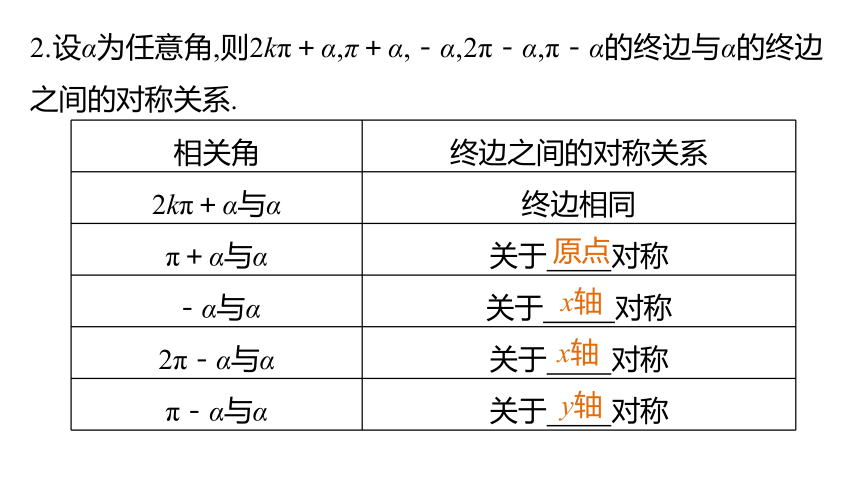
答 所有与α终边相同的角,连同α在内,可以构成一个集合:S={β|β=α+k·360°,k∈Z},即任何一个与角α终边相同的角,都可以表示成角α与整数个周角的和.[知识链接]2.设α为任意角,则2kπ+α,π+α,-α,2π-α,π-α的终边与α的终边之间的对称关系.原点x轴x轴y轴[预习导引]1.诱导公式一~四(其中k∈Z)
(1)公式一:sin(α+2kπ)= ,cos(α+2kπ)= ,
tan(α+2kπ)= .
(2)公式二:.sin(-α)= ,cos(-α)= ,
tan(-α)= .
(3)公式三:sin(π+α)= ,cos(π+α)= ,tan(π+α)= .
(4)公式四:sin(π-α)= ,cos(π-α)= ,tan(π-α)= .sin αcos αtan α-sin αcos α-tan α-sin α-cos αtan αsin α-cos α-tan α2.诱导公式一~四的记忆方法
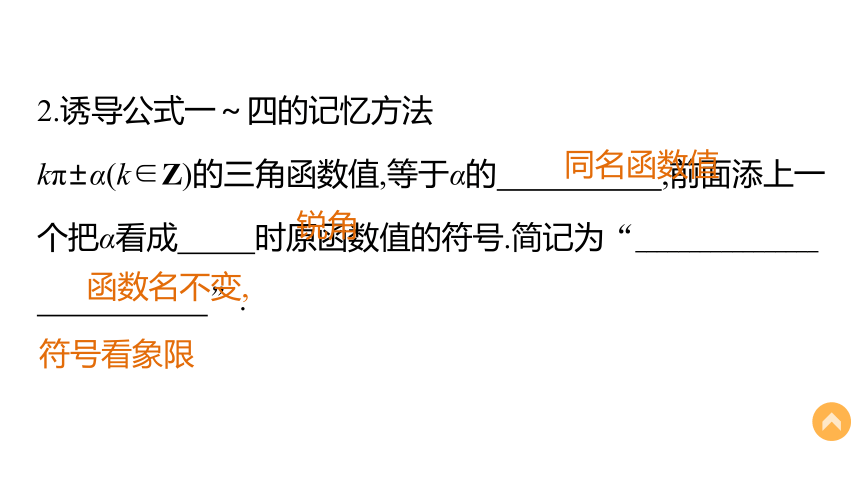
kπ±α(k∈Z)的三角函数值,等于α的 ,前面添上一个把α看成 时原函数值的符号.简记为“_________________
”.同名函数值锐角函数名不变,符号看象限要点一 给角求值问题例1 求下列各三角函数式的值:
(1)sin 1 320°;
解 方法一 sin 1 320°=sin (3×360°+240°)方法二 sin 1 320°=sin(4×360°-120°)=sin(-120°)(3)tan (-945°).
解 tan (-945°)=-tan 945°=-tan (225°+2×360°)
=-tan 225°=-tan (180°+45°)
=-tan 45°=-1.规律方法 此问题为已知角求值,主要是利用诱导公式把任意角的三角函数转化为锐角的三角函数求解.如果是负角,一般先将负角的三角函数化为正角的三角函数.解 ①当n为奇数时,②当n为偶数时,要点二 给值求值问题∴α-75°是第三象限角.规律方法 解答这类给值求值的问题,首先应把所给的值进行化简,再结合被求值的式子的特点,观察所给值的式子与被求式的特点,找出它们之间的内在联系,特别是角之间的关系,恰当地选择诱导公式.∴sin(α-3π)+cos(α-π)=-sin(3π-α)+cos(π-α)
=-sin(π-α)+(-cos α)
=-sin α-cos α=-(sin α+cos α)要点三 三角函数式的化简例3 化简下列各式:解 当k=2n(n∈Z)时,当k=2n+1(n∈Z)时,综上,原式=-1.规律方法 三角函数式的化简方法:
(1)利用诱导公式,将任意角的三角函数转化为锐角的三角函数.
(2)常用“切化弦”法,即表达式中的切函数通常化为弦函数.
(3)注意“1”的变式应用:如1=sin2 α+cos2α=tan .12341.求下列三角函数的值:
(1)sin 690°;
解 sin 690°=sin(360°+330°)=sin 330°
=sin(180°+150°)=-sin 150°=-sin(180°-30°)1234(3)tan(-1 845°).
解 tan(-1 845°)=tan(-5×360°-45°)=tan(-45°)
=-tan 45°=-1.123412341234证明 当n为偶数时,令n=2k,k∈Z,1234右边=(-1)2kcos α=cos α,
∴左边=右边.
当n为奇数时,令n=2k-1,k∈Z,1234右边=(-1)2k-1cos α=-cos α,
∴左边=右边.课堂小结1.明确各诱导公式的作用2.诱导公式的记忆
这四组诱导公式的记忆口诀是“函数名不变,符号看象限”.其含义是诱导公式两边的函数名称一致,符号则是将α看成锐角时原角所在象限的三角函数值的符号.α看成锐角,只是公式记忆的方便,实际上α可以是任意角.
3.2.3 诱导公式(一)[学习目标]1.了解三角函数的诱导公式的意义和作用.
2.理解诱导公式的推导过程.
3.能运用有关诱导公式解决一些三角函数的求值、化简和证明问题.1预习导学 挑战自我,点点落实2课堂讲义 重点难点,个个击破3当堂检测 当堂训练,体验成功1.对于任意一个角α,与它终边相同的角的集合应如何表示?
答 所有与α终边相同的角,连同α在内,可以构成一个集合:S={β|β=α+k·360°,k∈Z},即任何一个与角α终边相同的角,都可以表示成角α与整数个周角的和.[知识链接]2.设α为任意角,则2kπ+α,π+α,-α,2π-α,π-α的终边与α的终边之间的对称关系.原点x轴x轴y轴[预习导引]1.诱导公式一~四(其中k∈Z)
(1)公式一:sin(α+2kπ)= ,cos(α+2kπ)= ,
tan(α+2kπ)= .
(2)公式二:.sin(-α)= ,cos(-α)= ,
tan(-α)= .
(3)公式三:sin(π+α)= ,cos(π+α)= ,tan(π+α)= .
(4)公式四:sin(π-α)= ,cos(π-α)= ,tan(π-α)= .sin αcos αtan α-sin αcos α-tan α-sin α-cos αtan αsin α-cos α-tan α2.诱导公式一~四的记忆方法
kπ±α(k∈Z)的三角函数值,等于α的 ,前面添上一个把α看成 时原函数值的符号.简记为“_________________
”.同名函数值锐角函数名不变,符号看象限要点一 给角求值问题例1 求下列各三角函数式的值:
(1)sin 1 320°;
解 方法一 sin 1 320°=sin (3×360°+240°)方法二 sin 1 320°=sin(4×360°-120°)=sin(-120°)(3)tan (-945°).
解 tan (-945°)=-tan 945°=-tan (225°+2×360°)
=-tan 225°=-tan (180°+45°)
=-tan 45°=-1.规律方法 此问题为已知角求值,主要是利用诱导公式把任意角的三角函数转化为锐角的三角函数求解.如果是负角,一般先将负角的三角函数化为正角的三角函数.解 ①当n为奇数时,②当n为偶数时,要点二 给值求值问题∴α-75°是第三象限角.规律方法 解答这类给值求值的问题,首先应把所给的值进行化简,再结合被求值的式子的特点,观察所给值的式子与被求式的特点,找出它们之间的内在联系,特别是角之间的关系,恰当地选择诱导公式.∴sin(α-3π)+cos(α-π)=-sin(3π-α)+cos(π-α)
=-sin(π-α)+(-cos α)
=-sin α-cos α=-(sin α+cos α)要点三 三角函数式的化简例3 化简下列各式:解 当k=2n(n∈Z)时,当k=2n+1(n∈Z)时,综上,原式=-1.规律方法 三角函数式的化简方法:
(1)利用诱导公式,将任意角的三角函数转化为锐角的三角函数.
(2)常用“切化弦”法,即表达式中的切函数通常化为弦函数.
(3)注意“1”的变式应用:如1=sin2 α+cos2α=tan .12341.求下列三角函数的值:
(1)sin 690°;
解 sin 690°=sin(360°+330°)=sin 330°
=sin(180°+150°)=-sin 150°=-sin(180°-30°)1234(3)tan(-1 845°).
解 tan(-1 845°)=tan(-5×360°-45°)=tan(-45°)
=-tan 45°=-1.123412341234证明 当n为偶数时,令n=2k,k∈Z,1234右边=(-1)2kcos α=cos α,
∴左边=右边.
当n为奇数时,令n=2k-1,k∈Z,1234右边=(-1)2k-1cos α=-cos α,
∴左边=右边.课堂小结1.明确各诱导公式的作用2.诱导公式的记忆
这四组诱导公式的记忆口诀是“函数名不变,符号看象限”.其含义是诱导公式两边的函数名称一致,符号则是将α看成锐角时原角所在象限的三角函数值的符号.α看成锐角,只是公式记忆的方便,实际上α可以是任意角.
