17.2 勾股定理的逆定理(共32张)
文档属性
| 名称 | 17.2 勾股定理的逆定理(共32张) |  | |
| 格式 | zip | ||
| 文件大小 | 874.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-25 18:28:25 | ||
图片预览










文档简介
课件32张PPT。17.2 勾股定理的逆定理 如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2勾股定理的内容是什么?回顾旧知温故而知新:常见的勾股数
3 4 5
5 12 13
6 8 10
7 24 25
8 15 17
9 40 41
10 24 26
3 4 5
5 12 13
6 8 10
7 24 25
8 15 17
9 40 41
10 24 26
新课导入这个命题的条件和结论分别是什么?命题1 如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.条件:直角三角形的两直角边长为a,b,斜边长为c .结论:a2+b2=c2. 如果将条件和结论反过来,这个命题还成立吗?答案就藏在课本中,我们一起来看一看!学习目标 1.了解命题、逆命题等概念,并会写一个命题的逆命题.
2.会判断一个命题的逆命题的真假,知道定理与逆定理的关系.
3.了解勾股定理的逆定理的条件与结论与原命题的条件与结论的关系.
4.学会运用勾股定理的逆定理判别一个三角形是不是直角三角形.学习重、难点 重点:会分清一个命题的题设和结论,正确把握勾股定理与其逆定理的关系.
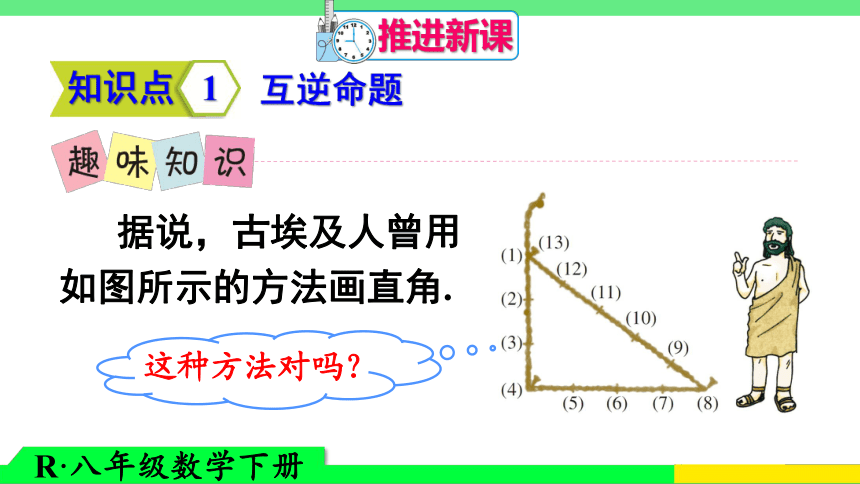
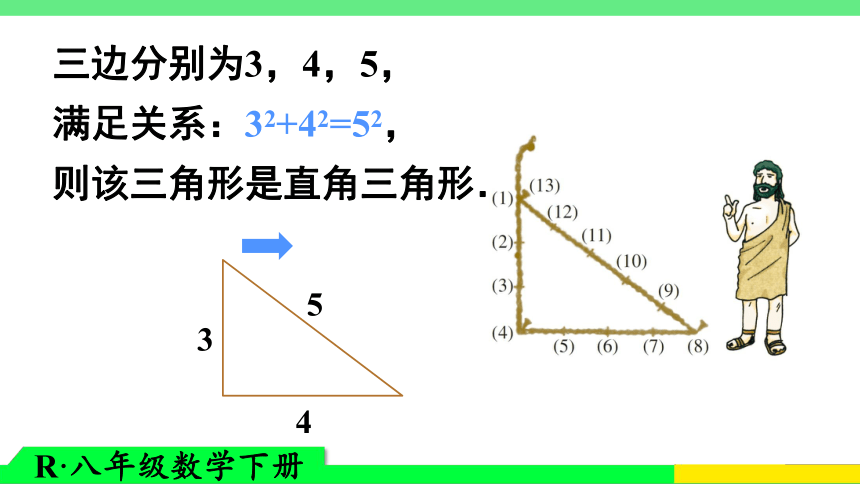
难点:勾股定理的逆定理的应用.推进新课知识点 1互逆命题 据说,古埃及人曾用如图所示的方法画直角.三边分别为3,4,5,
满足关系:32+42=52,
则该三角形是直角三角形.
画一画:下列各组数中的两数平方和等于第三数的平方,分别以这些数为边长画出三角形(单位:cm).
① 2.5,6,6.5; ② 6,8,10;
用量角器量一量,它们是什么三角形?直角三角形由前面几个例子,我们可以作出什么猜想?如果三角形ABC的三边长a,b,c满足a2+b2
=c2,那么这个三角形是直角三角形.命题1 如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.命题2 如果三角形ABC的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.这两个命题有什么不同?题设结论结论题设 我们把像这样,题设和结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题.说出下列命题的逆命题.这些逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相等;(1)内错角相等,两直线平行; 成立(2)如果两个实数的绝对值相等,那么这两个实数相等; 不成立知识点 2勾股定理的逆定理 命题2正确吗?如何证明呢??三角形全等 a证明:画一个△A'B'C',使∠ C'=90°,B'C'=a,C'A'=b.∵ ∠ C'=90°,∴ A'B'2= a2+b2=c2,∴ A'B' =c.∴ △ ABC ≌△ A'B'C'(SSS).∴ ∠C=∠C'=90°.BC=a=B'C',CA=b=C'A',AB=c=A'B'.在△ABC和△A'B'C'中勾股定理的逆定理
如果三角形ABC的三边长a,b,c满足a2+b2
=c2,那么这个三角形是直角三角形.作用:判定一个三角形三边满足什么条件时为直角三角形. 例1 判断由线段a,b,c组成的三角形是不是直角三角形:
(1)a=15,b=8,c=17;
(2)a=13,b=14,c=15.分析:只要看两条较小边长的平方和是否等于最大边长的平方. 解:(1) ∵ 152+82 =225+64=289,
172 =289,
∴ 152+82 =172.∴以15,8,17为边长的三角形是直角三角形. 像15,17,8 这样,能够成为直角三角形三条边长的三个正整数,称为勾股数. 解:(2) ∵132+142 =169+196=365,
152 =225,
∴132+142 ≠152.∴这个三角形不是直角三角形. 如果三条线段长a,b,c满足a2=c2-b2,这三条线段组成的三角形是不是直角三角形?为什么?解:这三条线段组成的三角形是直角三角形.
因为由 a2=c2-b2,所以有a2+b2=c2,由勾股定理的逆定理知这个三角形是直角三角形.知识点 3用勾股定理的逆定理解决实际问题例2 如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16n mile,“海
天”号每小时航行12n mile.它们离开
港口一个半小时后分别位于点Q、R
处,且相距30n mile.如果知道“远航”
号沿东北方向航行,能知道“海天”
号沿哪个方向航行吗?分析:1.求“海天”号的航向就是求 的角度.∠22.已知∠1的角度,则求出∠RPQ的
角度即可.3.根据已知条件可求出三边,利用勾股定理的逆定理判断∠RPQ是否为直角.解:根据题意,
PQ=16×1.5=24,
PR=12×1.5=18,QR=30.
因为242+182=302,
即PQ2+PR2=QR2,所以∠QPR=90°.
∠1=45°.因此∠2=45°,即“海天”号沿西北方向航行.随堂演练基础巩固1.下列各组数能否作为一个直角三角形的三边长?为什么?
(1) 5,12,13
(2) 6,8,10
(3) 15,20,25√√√2.写出下列命题的逆命题,并断定其逆命题的真假性.
如果两个角是直角,那么它们相等.
解:(1)如果两个角相等,那么这两个角是直角.假
命题.(2)在角的内部,角的平分线上的点到两边的距离相等.真命题.误 区 诊 断在△ABC中,a:b:c=9:15:12,试判断△ABC是直角三角形.错解:依题意,设 a=9k,b=15k,c=12k(k>0),
∵ a2+b2=(9k)2+(15k)2=306k2,c2=(12k)2=144k2,
∴ a2+b2≠c2,△ABC不是直角三角形.错因分析:错在没有弄清楚哪条边是最长边的情况下就盲目地运用勾股定理的逆定理,从而导致错误.正解:依题意知b是最长边,
设a=9k,b=15k,c=12k(k>0),
∵ a2+c2=(9k)2+(12k)2=225k2,b2=(15k)2=225k2,
∴ a2+c2 = b2,△ABC是直角三角形.课堂小结勾股定理的逆定理逆命题和逆定理勾股定理的逆定理勾股数1.习题17.2复习巩固1,2,3题;综合运用4,5题
2.完成练习册本课时的习题。课后作业谢谢大家!
3 4 5
5 12 13
6 8 10
7 24 25
8 15 17
9 40 41
10 24 26
3 4 5
5 12 13
6 8 10
7 24 25
8 15 17
9 40 41
10 24 26
新课导入这个命题的条件和结论分别是什么?命题1 如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.条件:直角三角形的两直角边长为a,b,斜边长为c .结论:a2+b2=c2. 如果将条件和结论反过来,这个命题还成立吗?答案就藏在课本中,我们一起来看一看!学习目标 1.了解命题、逆命题等概念,并会写一个命题的逆命题.
2.会判断一个命题的逆命题的真假,知道定理与逆定理的关系.
3.了解勾股定理的逆定理的条件与结论与原命题的条件与结论的关系.
4.学会运用勾股定理的逆定理判别一个三角形是不是直角三角形.学习重、难点 重点:会分清一个命题的题设和结论,正确把握勾股定理与其逆定理的关系.
难点:勾股定理的逆定理的应用.推进新课知识点 1互逆命题 据说,古埃及人曾用如图所示的方法画直角.三边分别为3,4,5,
满足关系:32+42=52,
则该三角形是直角三角形.
画一画:下列各组数中的两数平方和等于第三数的平方,分别以这些数为边长画出三角形(单位:cm).
① 2.5,6,6.5; ② 6,8,10;
用量角器量一量,它们是什么三角形?直角三角形由前面几个例子,我们可以作出什么猜想?如果三角形ABC的三边长a,b,c满足a2+b2
=c2,那么这个三角形是直角三角形.命题1 如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.命题2 如果三角形ABC的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.这两个命题有什么不同?题设结论结论题设 我们把像这样,题设和结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题.说出下列命题的逆命题.这些逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相等;(1)内错角相等,两直线平行; 成立(2)如果两个实数的绝对值相等,那么这两个实数相等; 不成立知识点 2勾股定理的逆定理 命题2正确吗?如何证明呢??三角形全等 a证明:画一个△A'B'C',使∠ C'=90°,B'C'=a,C'A'=b.∵ ∠ C'=90°,∴ A'B'2= a2+b2=c2,∴ A'B' =c.∴ △ ABC ≌△ A'B'C'(SSS).∴ ∠C=∠C'=90°.BC=a=B'C',CA=b=C'A',AB=c=A'B'.在△ABC和△A'B'C'中勾股定理的逆定理
如果三角形ABC的三边长a,b,c满足a2+b2
=c2,那么这个三角形是直角三角形.作用:判定一个三角形三边满足什么条件时为直角三角形. 例1 判断由线段a,b,c组成的三角形是不是直角三角形:
(1)a=15,b=8,c=17;
(2)a=13,b=14,c=15.分析:只要看两条较小边长的平方和是否等于最大边长的平方. 解:(1) ∵ 152+82 =225+64=289,
172 =289,
∴ 152+82 =172.∴以15,8,17为边长的三角形是直角三角形. 像15,17,8 这样,能够成为直角三角形三条边长的三个正整数,称为勾股数. 解:(2) ∵132+142 =169+196=365,
152 =225,
∴132+142 ≠152.∴这个三角形不是直角三角形. 如果三条线段长a,b,c满足a2=c2-b2,这三条线段组成的三角形是不是直角三角形?为什么?解:这三条线段组成的三角形是直角三角形.
因为由 a2=c2-b2,所以有a2+b2=c2,由勾股定理的逆定理知这个三角形是直角三角形.知识点 3用勾股定理的逆定理解决实际问题例2 如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16n mile,“海
天”号每小时航行12n mile.它们离开
港口一个半小时后分别位于点Q、R
处,且相距30n mile.如果知道“远航”
号沿东北方向航行,能知道“海天”
号沿哪个方向航行吗?分析:1.求“海天”号的航向就是求 的角度.∠22.已知∠1的角度,则求出∠RPQ的
角度即可.3.根据已知条件可求出三边,利用勾股定理的逆定理判断∠RPQ是否为直角.解:根据题意,
PQ=16×1.5=24,
PR=12×1.5=18,QR=30.
因为242+182=302,
即PQ2+PR2=QR2,所以∠QPR=90°.
∠1=45°.因此∠2=45°,即“海天”号沿西北方向航行.随堂演练基础巩固1.下列各组数能否作为一个直角三角形的三边长?为什么?
(1) 5,12,13
(2) 6,8,10
(3) 15,20,25√√√2.写出下列命题的逆命题,并断定其逆命题的真假性.
如果两个角是直角,那么它们相等.
解:(1)如果两个角相等,那么这两个角是直角.假
命题.(2)在角的内部,角的平分线上的点到两边的距离相等.真命题.误 区 诊 断在△ABC中,a:b:c=9:15:12,试判断△ABC是直角三角形.错解:依题意,设 a=9k,b=15k,c=12k(k>0),
∵ a2+b2=(9k)2+(15k)2=306k2,c2=(12k)2=144k2,
∴ a2+b2≠c2,△ABC不是直角三角形.错因分析:错在没有弄清楚哪条边是最长边的情况下就盲目地运用勾股定理的逆定理,从而导致错误.正解:依题意知b是最长边,
设a=9k,b=15k,c=12k(k>0),
∵ a2+c2=(9k)2+(12k)2=225k2,b2=(15k)2=225k2,
∴ a2+c2 = b2,△ABC是直角三角形.课堂小结勾股定理的逆定理逆命题和逆定理勾股定理的逆定理勾股数1.习题17.2复习巩固1,2,3题;综合运用4,5题
2.完成练习册本课时的习题。课后作业谢谢大家!
