人教八下数学 17.2勾股定理逆定理 课件(共21张)
文档属性
| 名称 | 人教八下数学 17.2勾股定理逆定理 课件(共21张) |  | |
| 格式 | ppt | ||
| 文件大小 | 855.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-25 18:27:17 | ||
图片预览





文档简介
(共21张PPT)
古埃及底比斯壁画(约公元前1415年)
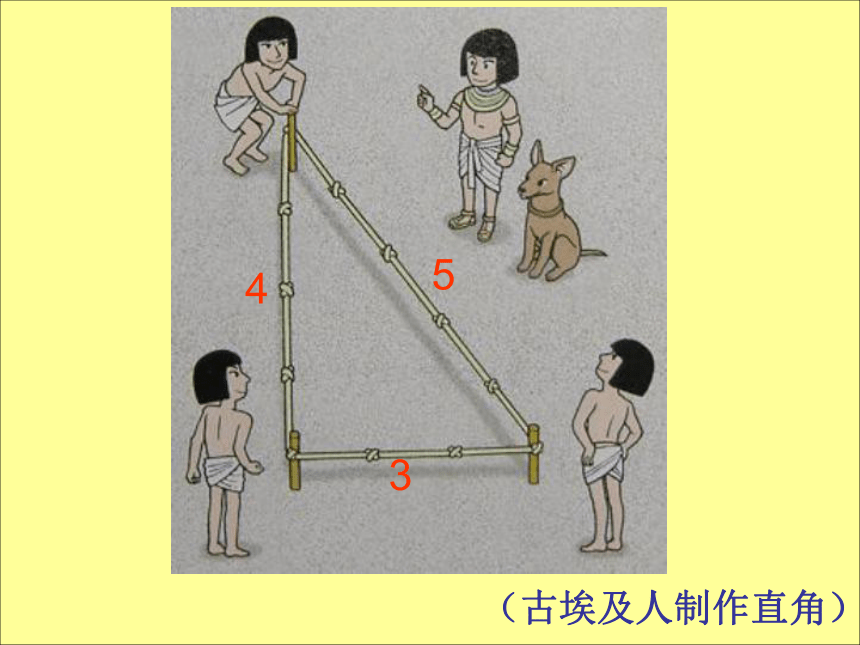
很多几何知识源自古埃及人的劳作。他们只用一根绳子就能确定直角。
不借助任何现代数学测量工具,试将一条绳子围成一个直角三角形。(绳子可以不用完)。
试一试
(古埃及人制作直角)
4
3
5
17.2 勾股定理的逆定理
——为古埃及人的做法揭密!
1.画图:画边长分别是下列各组数的三角形(单位:厘米)
A 3、4、3 B 3、4、5 C 3、4、6 D 6、8、10
3.测量:用你的量角器分别测量一下上述各三角形的最大
角的度数,并记录如下:
A _______ B _______ C ______ D _______
4.判断:请判断一下上述你所画的三角形的形状。
A _________ B _________ C ________ D _________
2.找关系:根据上述每个三角形所给的各组边长请你找出 最长边的平方与其他两边的平方和之间的关系 。 A _________ B ________ C _________ D ___________
活动一
锐角三角形
直角三角形
钝角三角形
直角三角形
32+32>42
32+42 < 62
32+42=52
62+82 =102
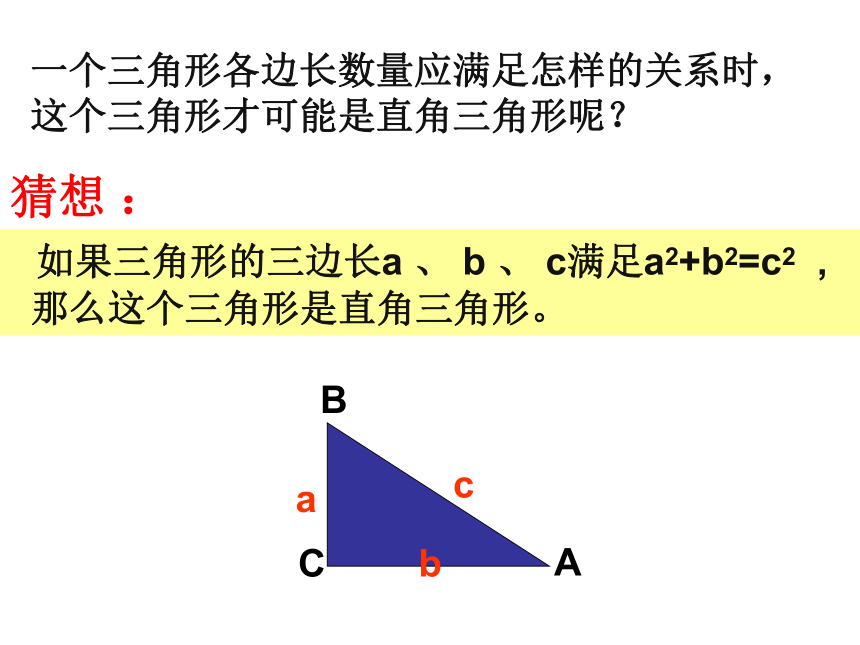
猜想 :
如果三角形的三边长a 、 b 、 c满足a2+b2=c2 ,
那么这个三角形是直角三角形。
一个三角形各边长数量应满足怎样的关系时,这个三角形才可能是直角三角形呢?
B
C
A
a
b
c
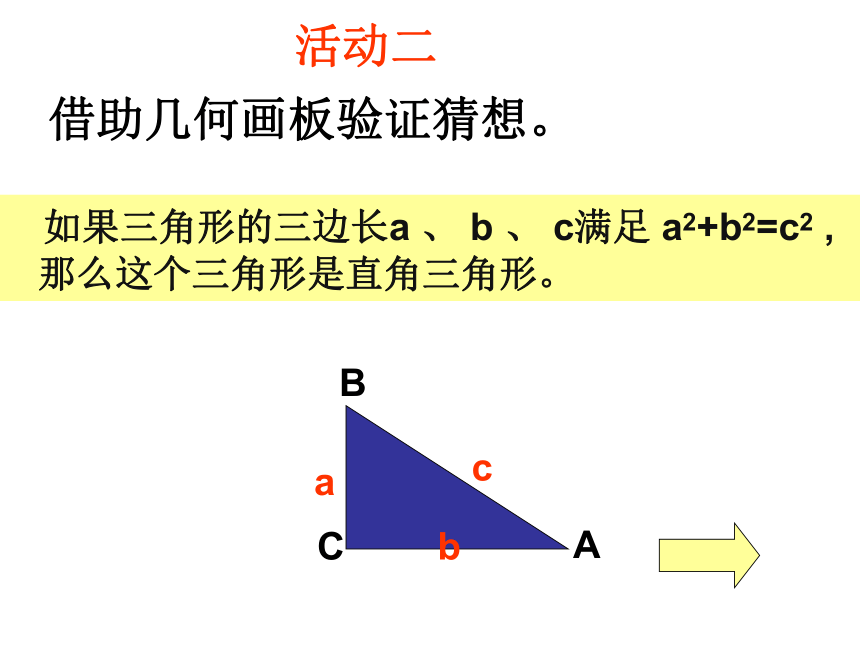
借助几何画板验证猜想。
活动二
如果三角形的三边长a 、 b 、 c满足 a2+b2=c2 ,
那么这个三角形是直角三角形。
B
C
A
a
b
c
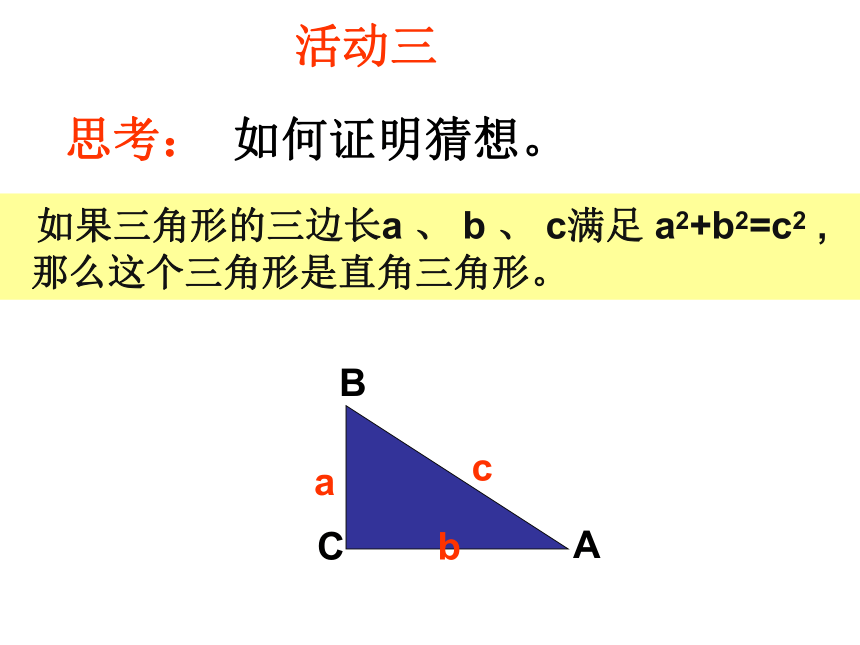
思考: 如何证明猜想。
活动三
如果三角形的三边长a 、 b 、 c满足 a2+b2=c2 ,
那么这个三角形是直角三角形。
B
C
A
a
b
c
B
C
A
证明:作Rt △A′B′C′,使∠C′ =900,
A′C′=AC=b,B′C′=BC=a(如图)
∴ A′B′2=a2+b2
∴ AB=A′B′
∴ △ABC≌ △A′B′C′(SSS).
∴ ∠C=∠C′= 900(全等三角形的对应边).
a
b
c
B′
C′
A′
a
b
已知:在△ABC中,AB=c ,AC=b ,BC=a,a2+b2=c2
求证: △ABC是直角三角形
=c2=AB2
∴ △ABC是直角三角形
2、如果三角形的三边长a 、 b 、 c满足 a2+b2=c2 ,
那么这个三角形是直角三角形。
B
C
A
a
b
c
活动四
1、如果直角三角形的两直角边长分别a 、 b , 斜边长为 c,那么 a2+b2=c2 。
观察以下两个命题,题设和结论有何关系
对在这两个命题中, 题设和结论正好相反放置,我们把这样的两个命题叫做互逆命题,如果把其中一个命题叫做原命题,那么另一个叫做它的逆命题。
再观察下面两组命题:
请说出上面两个命题的逆命题。
如果两个角是对顶角,那么它们相等。
三角形中相等的边所对的角相等。
它们都正确吗
想一想:一个命题是真命题,它的逆命题是真命 题还是假命题
如果两个角是对顶角,那么它们相等。
如果两个角相等,那么它们是对顶角。
三角形中相等的边所对的角相等。
三角形中相等的角所对的边相等。
一个命题的逆命题可能是真命题也可能是假命题。
正确
不正确
正确
正确
2、如果三角形的三边长a 、 b 、 c满足 a2+b2=c2 ,
那么这个三角形是直角三角形。
B
C
A
a
b
c
1、如果直角三角形的两直角边长分别a 、b,斜边长为 c,那么 a2+b2=c2 。
勾股定理
勾股定理的逆定理
一般地,如果一个定理的逆命题
经过证明是正确的,它也是一个
定理,则称两个定理互为逆定理。
这是判定直角三角形的根据之一
现在你能解释古埃及人的做法了吗?
例1、设三角形三边长分别为下列各组数,
试判断各三角形是否是直角三角形:
解: (1) ∵
∴该三角形是直角三角形
(2) ∵
∴该三角形是直角三角形
(3) ∵
∴该三角形不是直角三角形
(1)7,24,25;
(2)12,35,37;
(3)13,11,9。
例2、如图所示的三角形中,哪些是直角三角形,哪些不是,说说你的理由。
①
③
④
②
美国哥伦比亚大学普林顿收藏馆收藏了一块很古怪的泥板,这块泥板是在巴比伦挖掘出来的,编号322。考古学家相信这块泥板是公元前十八世纪的成品。泥板上有三列文字,没有人能解释。直至1945年,经过细心考察,才发现泥板上是三列数字。
考 古
你知道这些数字间的关系吗?借助计算器进行探索。
普林顿泥板
……
……
……
如果三角形的三边长a 、 b 、 c满足a2+b2=c2 ,
那么这个三角形是直角三角形。
1、勾股定理的逆定理
判定直角三角形
3、互逆命题
对在这两个命题中, 题设和结论正好相反,我
们把这样的两个命题叫做互逆命题。
2、勾股定理的逆定理的作用
4、勾股定理的逆定理的证明体现了从特殊到一
般、归纳的数学思想。
课堂回顾
想一想:
关于x、y、z的方程x2+y2=z2有没有正数解?
x2+y2=z2(x、y、z为正数)
以x、y、z为三边长的三角形是直角三角形(z最长)
古希腊数学家丢番图在《算术》中指出:关于x、y、z的方程x2+y2=z2有无数组正数解。
知识拓展
邮票上的费马与费马大定理
——同学们,学习前人的敢于思考、探索的精神,做科学知识的有心人吧!
古埃及底比斯壁画(约公元前1415年)
很多几何知识源自古埃及人的劳作。他们只用一根绳子就能确定直角。
不借助任何现代数学测量工具,试将一条绳子围成一个直角三角形。(绳子可以不用完)。
试一试
(古埃及人制作直角)
4
3
5
17.2 勾股定理的逆定理
——为古埃及人的做法揭密!
1.画图:画边长分别是下列各组数的三角形(单位:厘米)
A 3、4、3 B 3、4、5 C 3、4、6 D 6、8、10
3.测量:用你的量角器分别测量一下上述各三角形的最大
角的度数,并记录如下:
A _______ B _______ C ______ D _______
4.判断:请判断一下上述你所画的三角形的形状。
A _________ B _________ C ________ D _________
2.找关系:根据上述每个三角形所给的各组边长请你找出 最长边的平方与其他两边的平方和之间的关系 。 A _________ B ________ C _________ D ___________
活动一
锐角三角形
直角三角形
钝角三角形
直角三角形
32+32>42
32+42 < 62
32+42=52
62+82 =102
猜想 :
如果三角形的三边长a 、 b 、 c满足a2+b2=c2 ,
那么这个三角形是直角三角形。
一个三角形各边长数量应满足怎样的关系时,这个三角形才可能是直角三角形呢?
B
C
A
a
b
c
借助几何画板验证猜想。
活动二
如果三角形的三边长a 、 b 、 c满足 a2+b2=c2 ,
那么这个三角形是直角三角形。
B
C
A
a
b
c
思考: 如何证明猜想。
活动三
如果三角形的三边长a 、 b 、 c满足 a2+b2=c2 ,
那么这个三角形是直角三角形。
B
C
A
a
b
c
B
C
A
证明:作Rt △A′B′C′,使∠C′ =900,
A′C′=AC=b,B′C′=BC=a(如图)
∴ A′B′2=a2+b2
∴ AB=A′B′
∴ △ABC≌ △A′B′C′(SSS).
∴ ∠C=∠C′= 900(全等三角形的对应边).
a
b
c
B′
C′
A′
a
b
已知:在△ABC中,AB=c ,AC=b ,BC=a,a2+b2=c2
求证: △ABC是直角三角形
=c2=AB2
∴ △ABC是直角三角形
2、如果三角形的三边长a 、 b 、 c满足 a2+b2=c2 ,
那么这个三角形是直角三角形。
B
C
A
a
b
c
活动四
1、如果直角三角形的两直角边长分别a 、 b , 斜边长为 c,那么 a2+b2=c2 。
观察以下两个命题,题设和结论有何关系
对在这两个命题中, 题设和结论正好相反放置,我们把这样的两个命题叫做互逆命题,如果把其中一个命题叫做原命题,那么另一个叫做它的逆命题。
再观察下面两组命题:
请说出上面两个命题的逆命题。
如果两个角是对顶角,那么它们相等。
三角形中相等的边所对的角相等。
它们都正确吗
想一想:一个命题是真命题,它的逆命题是真命 题还是假命题
如果两个角是对顶角,那么它们相等。
如果两个角相等,那么它们是对顶角。
三角形中相等的边所对的角相等。
三角形中相等的角所对的边相等。
一个命题的逆命题可能是真命题也可能是假命题。
正确
不正确
正确
正确
2、如果三角形的三边长a 、 b 、 c满足 a2+b2=c2 ,
那么这个三角形是直角三角形。
B
C
A
a
b
c
1、如果直角三角形的两直角边长分别a 、b,斜边长为 c,那么 a2+b2=c2 。
勾股定理
勾股定理的逆定理
一般地,如果一个定理的逆命题
经过证明是正确的,它也是一个
定理,则称两个定理互为逆定理。
这是判定直角三角形的根据之一
现在你能解释古埃及人的做法了吗?
例1、设三角形三边长分别为下列各组数,
试判断各三角形是否是直角三角形:
解: (1) ∵
∴该三角形是直角三角形
(2) ∵
∴该三角形是直角三角形
(3) ∵
∴该三角形不是直角三角形
(1)7,24,25;
(2)12,35,37;
(3)13,11,9。
例2、如图所示的三角形中,哪些是直角三角形,哪些不是,说说你的理由。
①
③
④
②
美国哥伦比亚大学普林顿收藏馆收藏了一块很古怪的泥板,这块泥板是在巴比伦挖掘出来的,编号322。考古学家相信这块泥板是公元前十八世纪的成品。泥板上有三列文字,没有人能解释。直至1945年,经过细心考察,才发现泥板上是三列数字。
考 古
你知道这些数字间的关系吗?借助计算器进行探索。
普林顿泥板
……
……
……
如果三角形的三边长a 、 b 、 c满足a2+b2=c2 ,
那么这个三角形是直角三角形。
1、勾股定理的逆定理
判定直角三角形
3、互逆命题
对在这两个命题中, 题设和结论正好相反,我
们把这样的两个命题叫做互逆命题。
2、勾股定理的逆定理的作用
4、勾股定理的逆定理的证明体现了从特殊到一
般、归纳的数学思想。
课堂回顾
想一想:
关于x、y、z的方程x2+y2=z2有没有正数解?
x2+y2=z2(x、y、z为正数)
以x、y、z为三边长的三角形是直角三角形(z最长)
古希腊数学家丢番图在《算术》中指出:关于x、y、z的方程x2+y2=z2有无数组正数解。
知识拓展
邮票上的费马与费马大定理
——同学们,学习前人的敢于思考、探索的精神,做科学知识的有心人吧!
