19.1 多边形内角和课件(PPT16张)
文档属性
| 名称 | 19.1 多边形内角和课件(PPT16张) |
|
|
| 格式 | pptx | ||
| 文件大小 | 417.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-20 17:42:37 | ||
图片预览




文档简介
(共16张PPT)
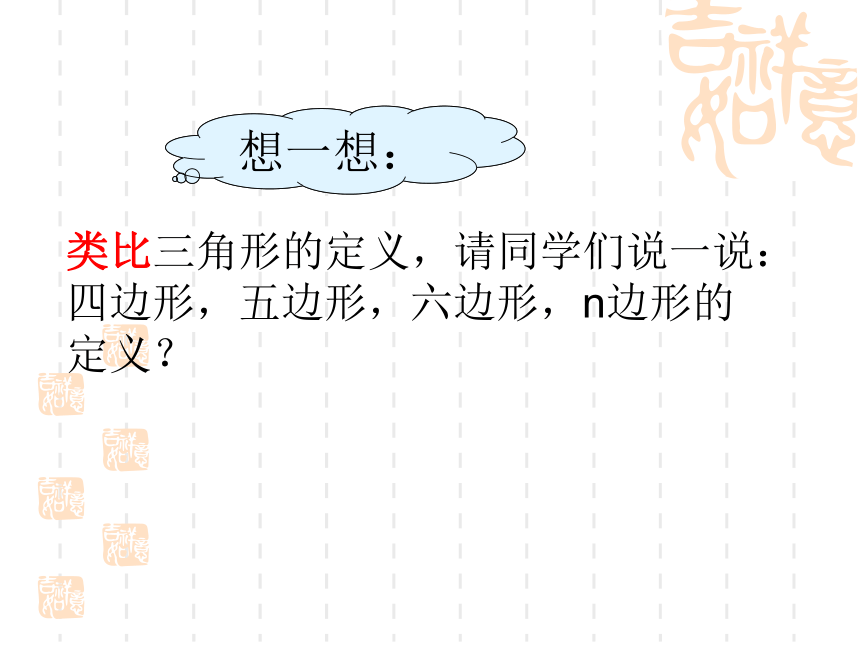
一个四边形的桌面,锯掉一个角后,
剩下的是什么图形?
想一想:
B
D
A
C
19.1多边形内角和
一:类比推理,得出概念:
判断题:
平面内,由三条线段组成的图形是三角形( )
于是,我们得出:
在平面内,由不在同一条直线上的三条线段首尾依次连接形成的封闭图形叫三角形
×
类比三角形的定义,请同学们说一说:四边形,五边形,六边形,n边形的定义?
想一想:
想一想:
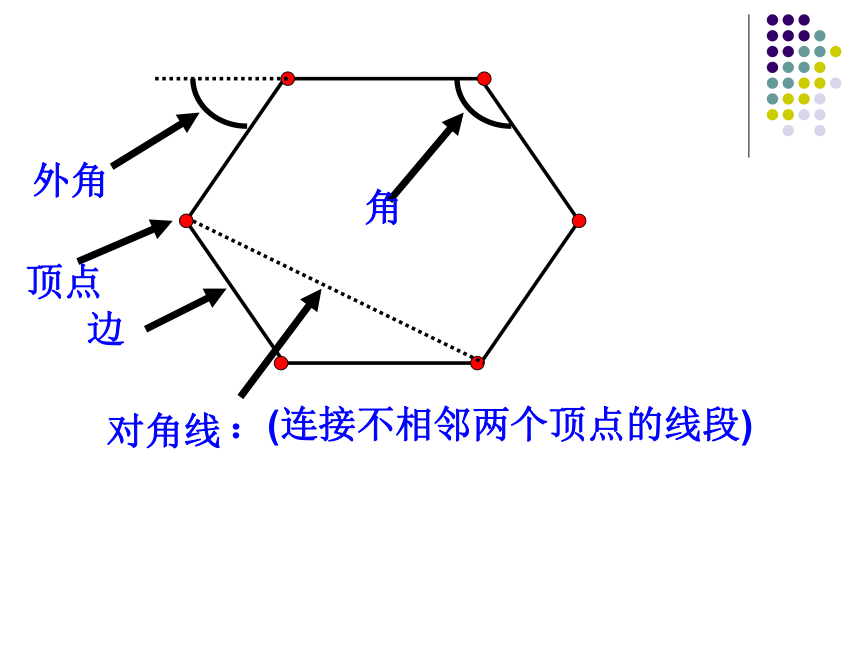
顶点
边
角
对角线
:(连接不相邻两个顶点的线段)
外角
于是,我们得出:
n边形有:n条边, n个角, n个顶点
一个多边形,如果把它任何一边双向延长,其他各边都在延长所得直线的同旁,这样的多边形 叫做凸多边形。
我们所研究的多边形都指凸多边形
凸四边形
凸五边形
凹四边形
比
一
比
二:动手操作,探索新知:
我们知道三角形内角和是180°,任意四边形内角和是360°,那么,五边形的内角和是多少度?
想一想:
按照第一种分割的做法来看:
填一填:
多边形边数 图形 分割成的三角形个数 多边形的内角和
4
5
6
... …… …… ……
n
2×1800
3×1800
4
4×1800
n-2
(n-2) ×1800
3
2
n边形的内角和公式:
(n-2)×180°
定理:
1、 (抢答) 8边形的内角和等于多少度?
(8-2) × 180°= 1080°
(10-2) × 180°= 1440°
三:随堂练习
2、十边形的内角和等于多少度?
4、一个多边形的内角和为7200,它是几边形?
3、一个多边形的内角和是18000,它是几边形
(n-2)×180°=18000,解得:n=12
(n-2)×180°= 7200 ,解得:n=6
四:提升练习
2008年奥运会在北京召开,设计一个内角和为2008度的多边形图案多有意义啊!
行吗?它是几边形?
五:课堂小结:
通过今天的学习,你在知识上有怎样的收获?在方法上有哪些收获?
六:作业
1、已知一个多边形各个内角都相等,都等于120°,求这个多边形的边数?
一个四边形的桌面,锯掉一个角后,
剩下的是什么图形?
想一想:
B
D
A
C
19.1多边形内角和
一:类比推理,得出概念:
判断题:
平面内,由三条线段组成的图形是三角形( )
于是,我们得出:
在平面内,由不在同一条直线上的三条线段首尾依次连接形成的封闭图形叫三角形
×
类比三角形的定义,请同学们说一说:四边形,五边形,六边形,n边形的定义?
想一想:
想一想:
顶点
边
角
对角线
:(连接不相邻两个顶点的线段)
外角
于是,我们得出:
n边形有:n条边, n个角, n个顶点
一个多边形,如果把它任何一边双向延长,其他各边都在延长所得直线的同旁,这样的多边形 叫做凸多边形。
我们所研究的多边形都指凸多边形
凸四边形
凸五边形
凹四边形
比
一
比
二:动手操作,探索新知:
我们知道三角形内角和是180°,任意四边形内角和是360°,那么,五边形的内角和是多少度?
想一想:
按照第一种分割的做法来看:
填一填:
多边形边数 图形 分割成的三角形个数 多边形的内角和
4
5
6
... …… …… ……
n
2×1800
3×1800
4
4×1800
n-2
(n-2) ×1800
3
2
n边形的内角和公式:
(n-2)×180°
定理:
1、 (抢答) 8边形的内角和等于多少度?
(8-2) × 180°= 1080°
(10-2) × 180°= 1440°
三:随堂练习
2、十边形的内角和等于多少度?
4、一个多边形的内角和为7200,它是几边形?
3、一个多边形的内角和是18000,它是几边形
(n-2)×180°=18000,解得:n=12
(n-2)×180°= 7200 ,解得:n=6
四:提升练习
2008年奥运会在北京召开,设计一个内角和为2008度的多边形图案多有意义啊!
行吗?它是几边形?
五:课堂小结:
通过今天的学习,你在知识上有怎样的收获?在方法上有哪些收获?
六:作业
1、已知一个多边形各个内角都相等,都等于120°,求这个多边形的边数?
