18.2.3 正方形课件
图片预览




文档简介
人教版数学八年级下册
18.2.3正方形
如图,某一拉门在完全关闭时,其相应的菱形变成
正方形.请说说图中∠1的变化过程.
正方形
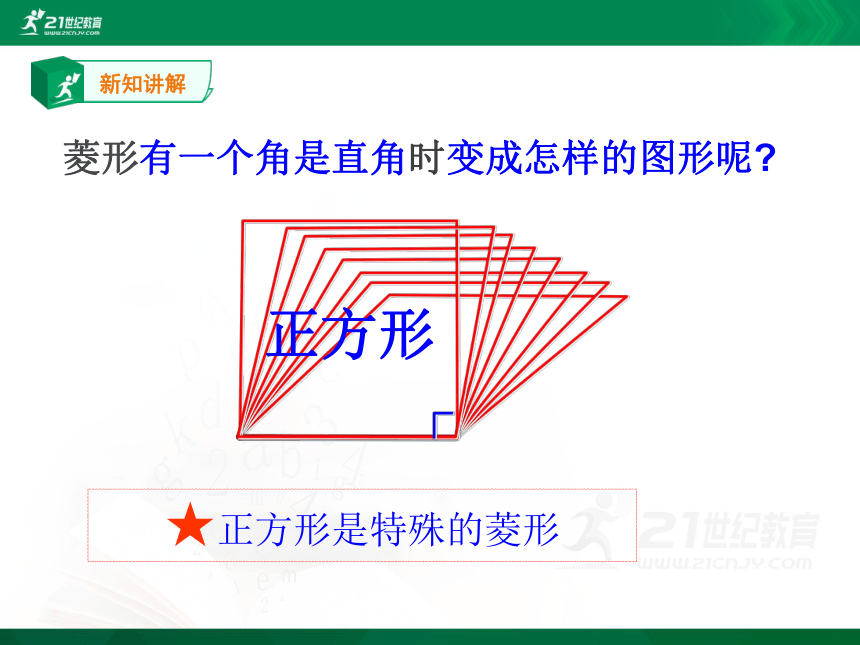
★正方形是特殊的菱形
菱形有一个角是直角时变成怎样的图形呢?
正方形
〃
〃
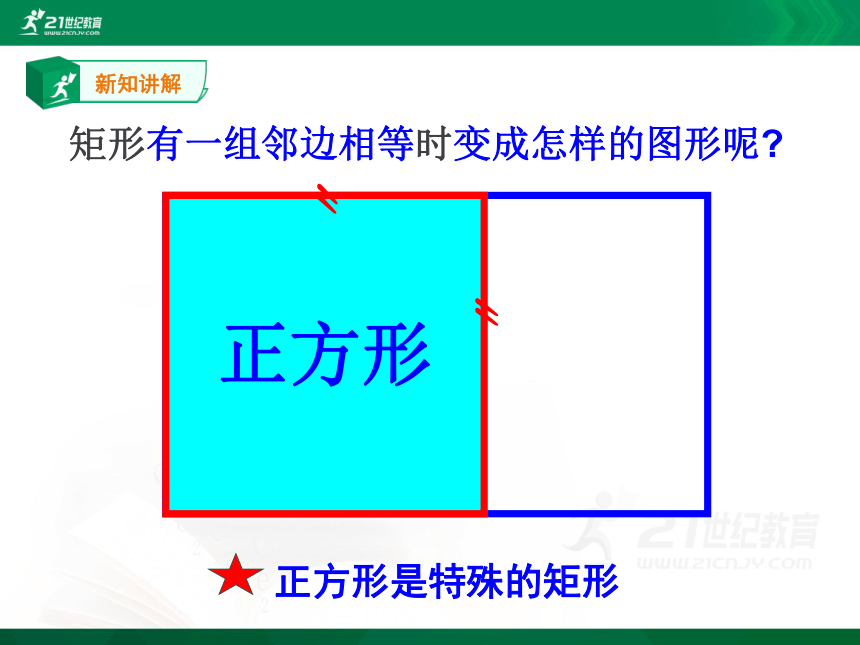
矩形有一组邻边相等时变成怎样的图形呢?
矩形
〃
〃
正方形
邻边
相等
〃
〃
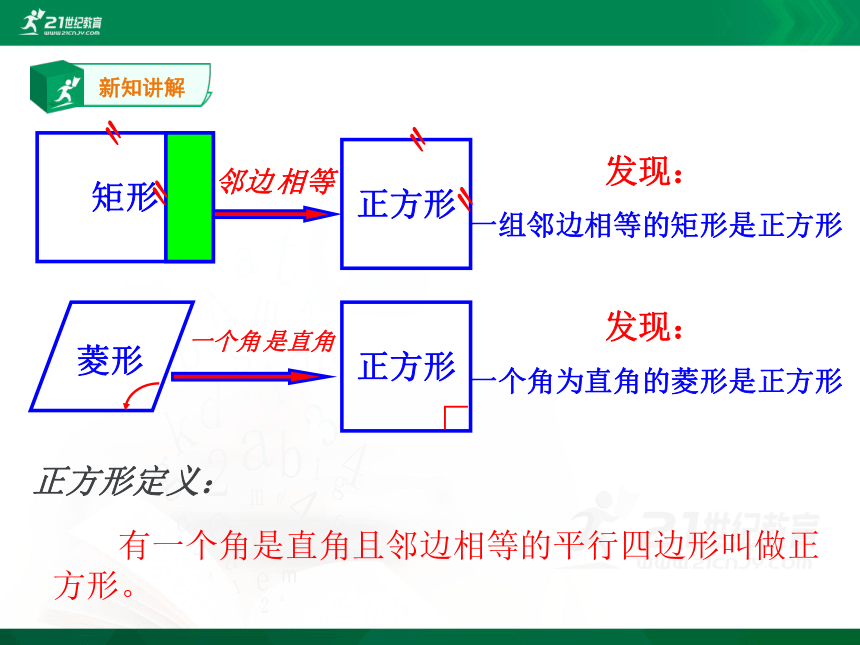
发现:
一组邻边相等的矩形是正方形
菱形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
正方形定义:
有一个角是直角且邻边相等的平行四边形叫做正方形。
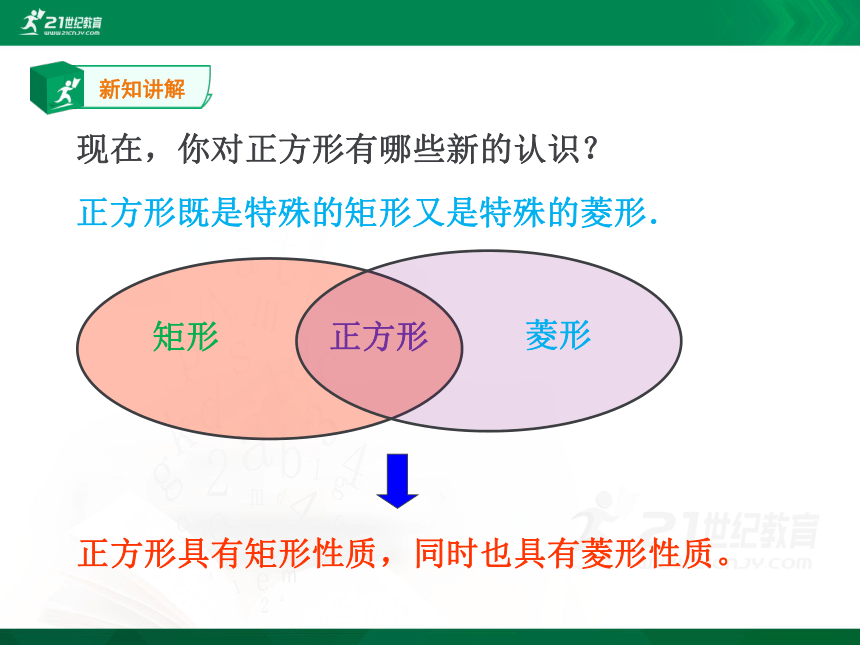
现在,你对正方形有哪些新的认识?
正方形
正方形具有矩形性质,同时也具有菱形性质。
正方形既是特殊的矩形又是特殊的菱形.
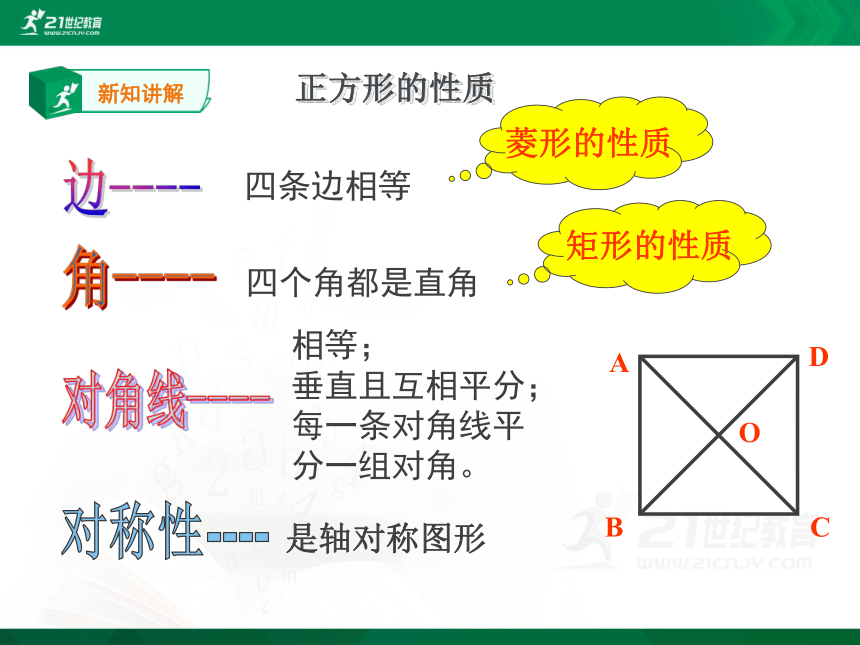
正方形的性质
四条边相等
四个角都是直角
相等;
垂直且互相平分;
每一条对角线平分一组对角。
A
B
C
D
O
是轴对称图形
根据图形所具有的性质,在下表相应的空格中打”√”
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
正方形不但具备一般的平行四边形的性质,而且同时具备矩形和菱形的性质。
平行四边形 矩形 菱形 正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
例1 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形。
已知: 如图,四边形ABCD是正方形,对角
线AC、BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
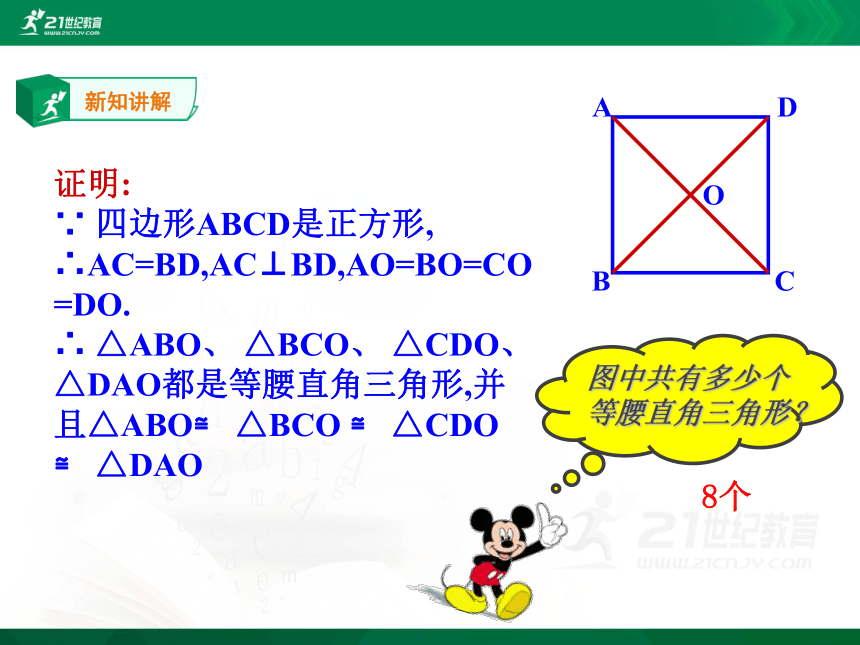
证明:
∵ 四边形ABCD是正方形,
∴AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且△ABO≌ △BCO ≌ △CDO ≌ △DAO
8个
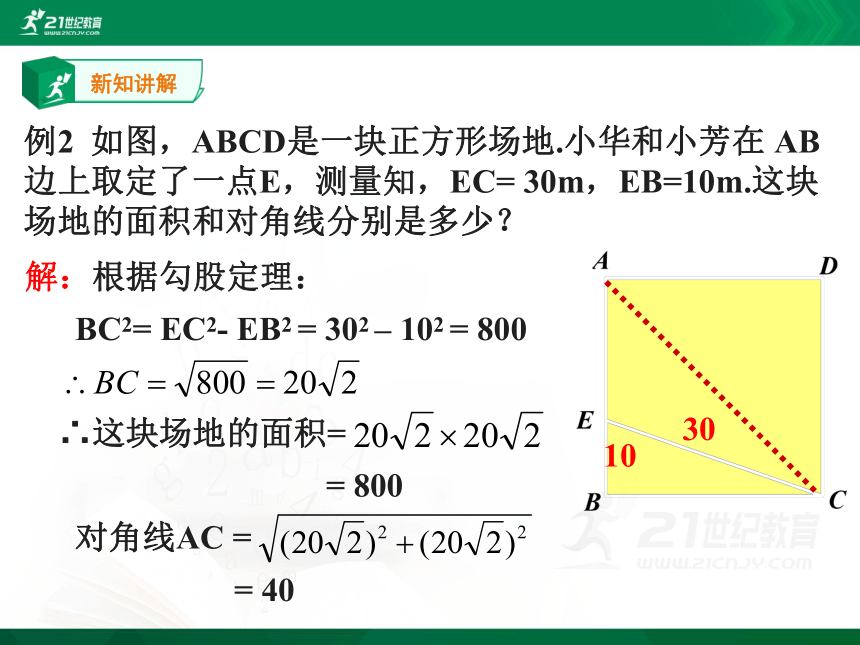
例2 如图,ABCD是一块正方形场地.小华和小芳在 AB边上取定了一点E,测量知,EC= 30m,EB=10m.这块场地的面积和对角线分别是多少?
30
10
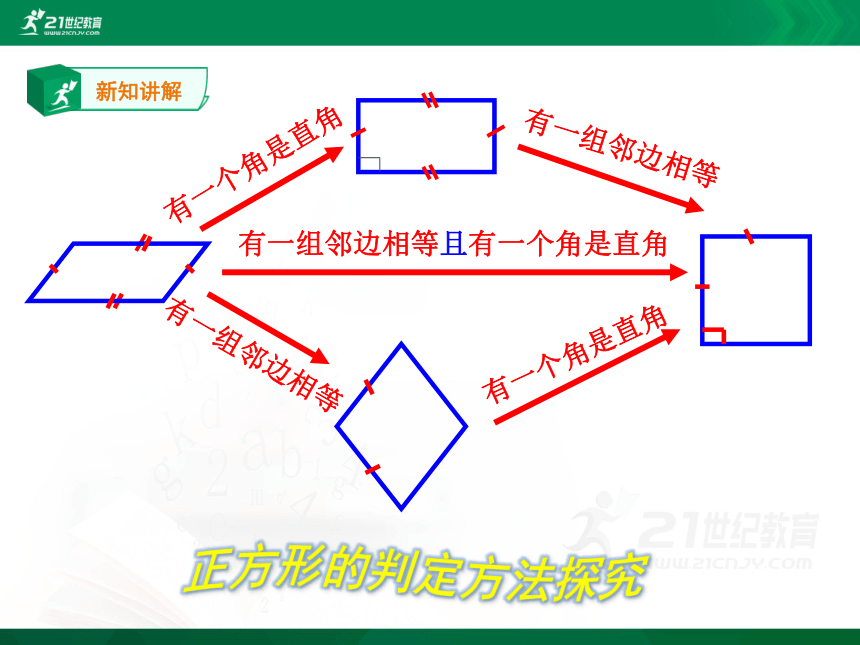
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
(1)如果一个菱形的两条对角线相等,那么它一定是正方形.
(2)如果一个矩形的两条对角线互相垂直,那么它一定是正方形.
(3)两条对角线互相垂直平分且相等的四边形,一定是正方形.
(4)四条边相等,且有一个角是直角的四边形是正方形.
例3 (1)要使一个菱形成为正方形需增加的条件是 。
(2)要使一个矩形成为正方形需添加的条件是 。
?
?
?
?
判断正误:
例4 已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.
证明:∵∠C=90°,
DE⊥BC于E,DF⊥AC于F
∴四边形CEDF有三个直角,
它是矩形
又∵CD平分∠ACB
∴ DE=DF
∴四边形CEDF是正方形
练习 如图,已知Rt△ABC中,∠C=900,∠A、∠B的角平分线相交于点D,DE⊥BC于点E,DF⊥AC于点F。求证:四边形AEDF是正方形。
D
A
B
C
E
F
M
例5 在正方形ABCD中,点A′、B′、C′、D′分别是AB、BC、CD、DA的中点,四边形A′B′C′D′是正方形吗?为什么?
A
B
C
D
D′
C′
B′
A′
练习 正方形ABCD中,点A′,B′,C′,D′分别在AB,BC,CD,DA上,且AA′=BB′=CC′=DD′.
四边形A′B′C′D′是正方形吗?为什么?
①由已知正方形证
三角形全等;
②证得菱形;
③再证直角;
④是正方形。
证题思路分析
例6 正方形ABCD中,对角线AC和BD交于点 O,点A′,B′,C′,D′分别是AO,BO,CO,DO的中点,判断四边形A′B′C′D′的形状并说明理由。
A
B
C
D
D′
C′
B′
A′
O
变式 正方形ABCD中,对角线AC和BD交于点O,点A′,B′,C′,D′分别在AC、BD上,且AA′=BB′=CC′=DD′.判断四边形A′B′C′D′的形状并说明理由。
A
B
D
D′
C′
B′
A′
O
C
例7 如图,△ABC的外面作正
方形ABDE和ACFG,连结BG、
CE,交点为N。 (1)求证:∠CEA=∠ABG (2)判断CE与BG的关系并证明。
证明:∵四边形ABDE和四边形ACFG是正方形 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG
变式1 如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG,M是BC的中点.
求证:⑴CE=BG;⑵EG=2AM.
根据正方形的四边相等,得AD=CD
变式2 如图四边形ABCD和DEFG都是正方形,试说明AE=CG。
解:
因为四边形ABCD是正方形
又知四边形DEFG也是正方形
所以DE=DG
又因为正方形的每个内角为90°
所以∠ADE+∠EDC=∠CDG+∠EDC
所以∠ADE=∠CDG
所以三角形ADE可以看成是由三角形CDG绕着点D顺时针
旋转 90° 得到。⊿AED≌ ⊿CGD
所以AE=CG
如何设计花坛?
例8 在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
请你当设计师
A
B
C
D
E
F
G
H
O
例9 如图,正方形OPQR的一个顶点O是边长为2的正方形ABCD对角线AC与BD的交点,则两正方形重合部分的面积是 。
A D
B C
O
P
Q
R
1. 正方形的四条边都相等.
2. 正方形的四个角都相等.
3. 正方形的对角线互相垂直平分且相等,且每一条对角线平分一组对角.
4. 正方形是轴对称图形,有4条对称轴.
一组邻边相等,并且有一个角是直角的平行四边形叫做正方形。
1.判断对错:
(1) 四边相等的四边形是正方形
(2)四角相等的四边形是正方形
(3)对角线垂直的平行四边形是正方形
(4)对角线互相垂直平分且相等的四边形是正方形
(5)四条边相等且有一个角是直角的四边形是正方形
√
×
×
×
√
2.正方形具有而矩形不一定具有的性质是( )
A、四个角相等. B、对角线互相垂直平分.
C、对角互补. D、对角线相等.
3.正方形具有而菱形不一定具有的性质( )
A、四条边相等. B、对角线互相垂直平分.
C、对角线平分一组对角. D、对角线相等.
B
D
4.下列判断中正确的是( )
A、四边相等的四边形是正方形
B、四角相等的四边形是正方形
C、对角线垂直的平行四边形是正方形
D、对角线互相垂直平分且相等的四边形是正方形
D
5.在四边形ABCD中O是对角线的交点,能判定这个四边形是正方形的是( ) A、AC = BD,AB∥CD,AB = CD B、AD∥BC,∠A =∠ C C、AO=BO=CO=DO,AC⊥BD D、AO=CO,BO=DO,AB=BC
C
7.一正方形对角线长为4,则它的面积为 .
6.一正方形边长为4,则它的面积为 .
8
16
8.如图,正方形ABCD的面积是9cm2。则AB= cm, AC= cm。
3
9.为什么下列三个图形都是正方形?
有一组邻边相等并且有一个角是直角的平行四边形是正方形。
既是矩形又是菱形的四边形是正方形。
两条对角线互相垂直平分且相等的四边形是正方形。
10.正方形ABCD中∠DAF=25°,AF交对角线BD于E,交CD于F,求∠BEC的度数.
若∠FEC=30°则∠DAF= 。
30°
∠BEC= ∠BEA= ∠DAF+ ∠ADE= 30°+ 45°= 75°
11.如图,四边形ABCD是正方形,延长BC到E,使CE=AC,连接AE,交CD于F,求∠AFC的度数.
12.矩形ABCD中,四个内角的平分线组成四边形EMFN,判断四边形EMFN的形状,并说明原因。
13.在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
14.如图,E、F分别在正方形ABCD的边BC、CD上,且∠EAF=45°。试说明:EF=BE+DF
A
B
C
D
E
F
15.如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.求证:(1)AE=AF;(2)EA⊥AF.
(2)∵∠2+∠3=90 °
∴∠1+∠2=90 °
∴ EA⊥FA
证明:
16.如图所示,正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F。试说明:AP=EF。
解:
连接PC
∵PE⊥BC , PF⊥DC
而四边形ABCD是正方形
∴∠FCE=90°
∴四边形PECF是矩形
∴PC=EF
又∵四边形BAPC是以BD为轴的轴对称图形
∴AP=PC
∴AP=EF
17.如图,正方形ABCD中,AC、BD相交于O,MN∥
AB且MN分别交OA、OB于M、N,求证:BM=CN。
证明:
∵四边形ABCD是正方形 ∴OA=OB ,
∠1=∠2=∠3=45° 又∵MN∥AB
∴∠OMN=∠1=∠3
=∠ONM=45° ∴OM=ON ∴OA-OM=OB-ON 即AM=BN
18.已知:如图在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M。
求证:∠MFD=45°
证明:
∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF(AAS) ∴DM=DF
2.选做题:教材习题18.2第7、15题.
1.必做题:习题18.2,第12、13题.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
18.2.3正方形
如图,某一拉门在完全关闭时,其相应的菱形变成
正方形.请说说图中∠1的变化过程.
正方形
★正方形是特殊的菱形
菱形有一个角是直角时变成怎样的图形呢?
正方形
〃
〃
矩形有一组邻边相等时变成怎样的图形呢?
矩形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形是正方形
菱形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
正方形定义:
有一个角是直角且邻边相等的平行四边形叫做正方形。
现在,你对正方形有哪些新的认识?
正方形
正方形具有矩形性质,同时也具有菱形性质。
正方形既是特殊的矩形又是特殊的菱形.
正方形的性质
四条边相等
四个角都是直角
相等;
垂直且互相平分;
每一条对角线平分一组对角。
A
B
C
D
O
是轴对称图形
根据图形所具有的性质,在下表相应的空格中打”√”
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
正方形不但具备一般的平行四边形的性质,而且同时具备矩形和菱形的性质。
平行四边形 矩形 菱形 正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
例1 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形。
已知: 如图,四边形ABCD是正方形,对角
线AC、BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明:
∵ 四边形ABCD是正方形,
∴AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且△ABO≌ △BCO ≌ △CDO ≌ △DAO
8个
例2 如图,ABCD是一块正方形场地.小华和小芳在 AB边上取定了一点E,测量知,EC= 30m,EB=10m.这块场地的面积和对角线分别是多少?
30
10
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
(1)如果一个菱形的两条对角线相等,那么它一定是正方形.
(2)如果一个矩形的两条对角线互相垂直,那么它一定是正方形.
(3)两条对角线互相垂直平分且相等的四边形,一定是正方形.
(4)四条边相等,且有一个角是直角的四边形是正方形.
例3 (1)要使一个菱形成为正方形需增加的条件是 。
(2)要使一个矩形成为正方形需添加的条件是 。
?
?
?
?
判断正误:
例4 已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.
证明:∵∠C=90°,
DE⊥BC于E,DF⊥AC于F
∴四边形CEDF有三个直角,
它是矩形
又∵CD平分∠ACB
∴ DE=DF
∴四边形CEDF是正方形
练习 如图,已知Rt△ABC中,∠C=900,∠A、∠B的角平分线相交于点D,DE⊥BC于点E,DF⊥AC于点F。求证:四边形AEDF是正方形。
D
A
B
C
E
F
M
例5 在正方形ABCD中,点A′、B′、C′、D′分别是AB、BC、CD、DA的中点,四边形A′B′C′D′是正方形吗?为什么?
A
B
C
D
D′
C′
B′
A′
练习 正方形ABCD中,点A′,B′,C′,D′分别在AB,BC,CD,DA上,且AA′=BB′=CC′=DD′.
四边形A′B′C′D′是正方形吗?为什么?
①由已知正方形证
三角形全等;
②证得菱形;
③再证直角;
④是正方形。
证题思路分析
例6 正方形ABCD中,对角线AC和BD交于点 O,点A′,B′,C′,D′分别是AO,BO,CO,DO的中点,判断四边形A′B′C′D′的形状并说明理由。
A
B
C
D
D′
C′
B′
A′
O
变式 正方形ABCD中,对角线AC和BD交于点O,点A′,B′,C′,D′分别在AC、BD上,且AA′=BB′=CC′=DD′.判断四边形A′B′C′D′的形状并说明理由。
A
B
D
D′
C′
B′
A′
O
C
例7 如图,△ABC的外面作正
方形ABDE和ACFG,连结BG、
CE,交点为N。 (1)求证:∠CEA=∠ABG (2)判断CE与BG的关系并证明。
证明:∵四边形ABDE和四边形ACFG是正方形 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG
变式1 如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG,M是BC的中点.
求证:⑴CE=BG;⑵EG=2AM.
根据正方形的四边相等,得AD=CD
变式2 如图四边形ABCD和DEFG都是正方形,试说明AE=CG。
解:
因为四边形ABCD是正方形
又知四边形DEFG也是正方形
所以DE=DG
又因为正方形的每个内角为90°
所以∠ADE+∠EDC=∠CDG+∠EDC
所以∠ADE=∠CDG
所以三角形ADE可以看成是由三角形CDG绕着点D顺时针
旋转 90° 得到。⊿AED≌ ⊿CGD
所以AE=CG
如何设计花坛?
例8 在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
请你当设计师
A
B
C
D
E
F
G
H
O
例9 如图,正方形OPQR的一个顶点O是边长为2的正方形ABCD对角线AC与BD的交点,则两正方形重合部分的面积是 。
A D
B C
O
P
Q
R
1. 正方形的四条边都相等.
2. 正方形的四个角都相等.
3. 正方形的对角线互相垂直平分且相等,且每一条对角线平分一组对角.
4. 正方形是轴对称图形,有4条对称轴.
一组邻边相等,并且有一个角是直角的平行四边形叫做正方形。
1.判断对错:
(1) 四边相等的四边形是正方形
(2)四角相等的四边形是正方形
(3)对角线垂直的平行四边形是正方形
(4)对角线互相垂直平分且相等的四边形是正方形
(5)四条边相等且有一个角是直角的四边形是正方形
√
×
×
×
√
2.正方形具有而矩形不一定具有的性质是( )
A、四个角相等. B、对角线互相垂直平分.
C、对角互补. D、对角线相等.
3.正方形具有而菱形不一定具有的性质( )
A、四条边相等. B、对角线互相垂直平分.
C、对角线平分一组对角. D、对角线相等.
B
D
4.下列判断中正确的是( )
A、四边相等的四边形是正方形
B、四角相等的四边形是正方形
C、对角线垂直的平行四边形是正方形
D、对角线互相垂直平分且相等的四边形是正方形
D
5.在四边形ABCD中O是对角线的交点,能判定这个四边形是正方形的是( ) A、AC = BD,AB∥CD,AB = CD B、AD∥BC,∠A =∠ C C、AO=BO=CO=DO,AC⊥BD D、AO=CO,BO=DO,AB=BC
C
7.一正方形对角线长为4,则它的面积为 .
6.一正方形边长为4,则它的面积为 .
8
16
8.如图,正方形ABCD的面积是9cm2。则AB= cm, AC= cm。
3
9.为什么下列三个图形都是正方形?
有一组邻边相等并且有一个角是直角的平行四边形是正方形。
既是矩形又是菱形的四边形是正方形。
两条对角线互相垂直平分且相等的四边形是正方形。
10.正方形ABCD中∠DAF=25°,AF交对角线BD于E,交CD于F,求∠BEC的度数.
若∠FEC=30°则∠DAF= 。
30°
∠BEC= ∠BEA= ∠DAF+ ∠ADE= 30°+ 45°= 75°
11.如图,四边形ABCD是正方形,延长BC到E,使CE=AC,连接AE,交CD于F,求∠AFC的度数.
12.矩形ABCD中,四个内角的平分线组成四边形EMFN,判断四边形EMFN的形状,并说明原因。
13.在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
14.如图,E、F分别在正方形ABCD的边BC、CD上,且∠EAF=45°。试说明:EF=BE+DF
A
B
C
D
E
F
15.如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.求证:(1)AE=AF;(2)EA⊥AF.
(2)∵∠2+∠3=90 °
∴∠1+∠2=90 °
∴ EA⊥FA
证明:
16.如图所示,正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F。试说明:AP=EF。
解:
连接PC
∵PE⊥BC , PF⊥DC
而四边形ABCD是正方形
∴∠FCE=90°
∴四边形PECF是矩形
∴PC=EF
又∵四边形BAPC是以BD为轴的轴对称图形
∴AP=PC
∴AP=EF
17.如图,正方形ABCD中,AC、BD相交于O,MN∥
AB且MN分别交OA、OB于M、N,求证:BM=CN。
证明:
∵四边形ABCD是正方形 ∴OA=OB ,
∠1=∠2=∠3=45° 又∵MN∥AB
∴∠OMN=∠1=∠3
=∠ONM=45° ∴OM=ON ∴OA-OM=OB-ON 即AM=BN
18.已知:如图在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M。
求证:∠MFD=45°
证明:
∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF(AAS) ∴DM=DF
2.选做题:教材习题18.2第7、15题.
1.必做题:习题18.2,第12、13题.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
