2018-2019学年重庆市南岸区南开(融侨)中学九年级(下)开学数学试卷(解析版)
文档属性
| 名称 | 2018-2019学年重庆市南岸区南开(融侨)中学九年级(下)开学数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1002.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-19 14:14:41 | ||
图片预览


文档简介
2018-2019学年重庆市南岸区南开(融侨)中学九年级(下)开学数学试卷
一、选择题1(本人题共12个小题,每小题4分,其4分)在每个小题的卜面,都给出了代为A,BC、D的四个答,其中只有个是正确的,请将每小的首案直接在答题卡中对应的方格中
1.(4分)﹣2的倒数是( )
A.﹣ B. C.2 D.﹣2
2.(4分)下列电视台图标中,属于中心对称图形的是( )
A. B.
C. D.
3.(4分)在平面直角坐标系中,点M(﹣2,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(4分)△ABC三边长分别为a、b、c,则下列条件不能判断△ABC是直角三角形的是( )
A.a=3,b=4,c=5 B.a=4,b=5,c=6
C.a=6,b=8,c=10 D.a=5,b=12,c=13
5.(4分)下列命题中,是真命题的是( )
A.同位角相等
B.相等的角是对顶角
C.邻补角一定互补
D.有且只有一条直线与已知直线垂直
6.(4分)下列不等式的变形不正确的是( )
A.若a>b,则a+3>b+3 B.若﹣a>﹣b则a<b:
C.若﹣x<y,则x>﹣2y D.若﹣2x>a,则x>﹣a
7.(4分)已知?ABCD的周长是22,△ABC的周长是17,则AC的长为( )
A.5 B.6 C.7 D.8
8.(4分)估计(2﹣)?的值应在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
9.(4分)在关于x的函数y=+(x﹣1)0中,自变量x的取值范图是( )
A.x≥﹣2 B.x≥﹣2且x≠0 C.x≥﹣2且x≠1 D.x≥1
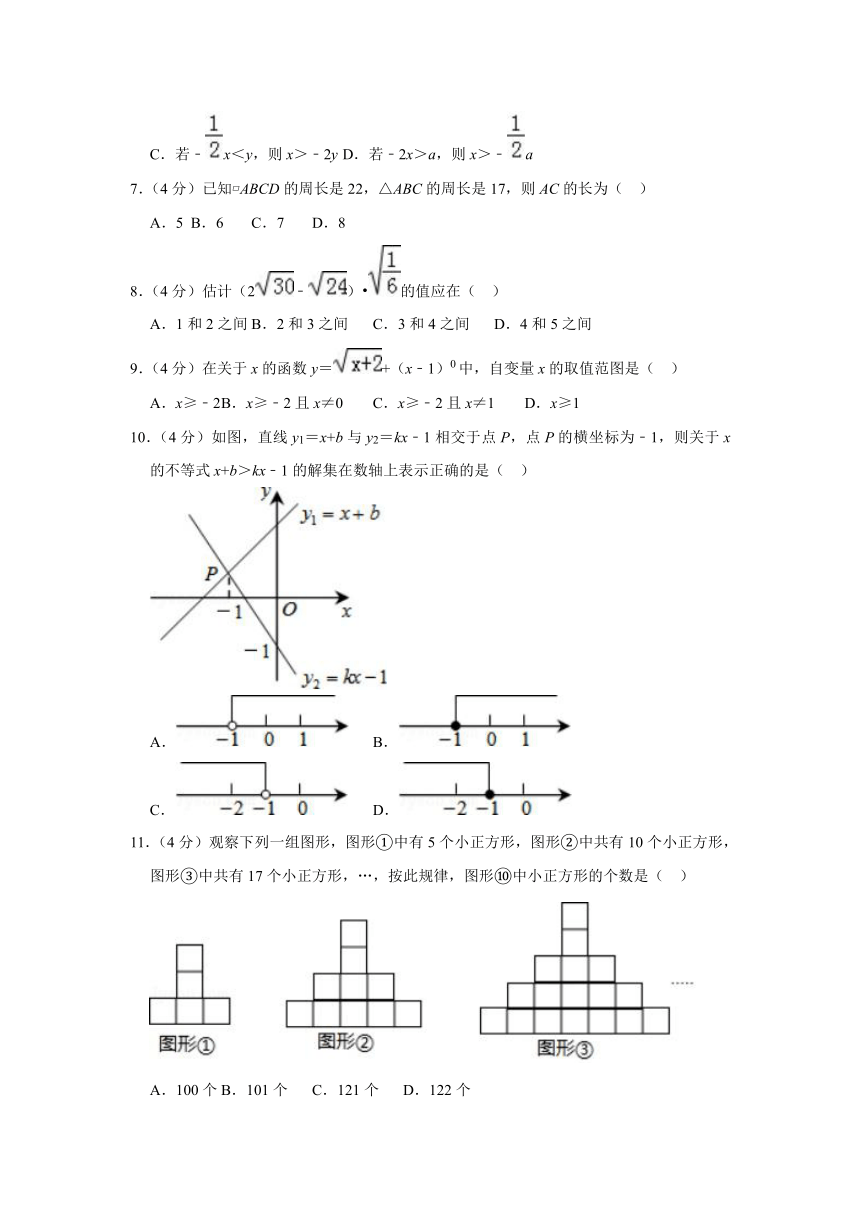
10.(4分)如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是( )
A. B.
C. D.
11.(4分)观察下列一组图形,图形①中有5个小正方形,图形②中共有10个小正方形,图形③中共有17个小正方形,…,按此规律,图形⑩中小正方形的个数是( )
A.100个 B.101个 C.121个 D.122个
12.(4分)已知整数k使得关于x、y的二元一次方程组的解为正整数,且关于x的不等式组有且仅有四个整数解,则所有满足条件的k的和为( )
A.4 B.9 C.10 D.12
二、填空题,(本大题共9个小题,每小3分,共27分)
13.(3分)已知y=xa﹣1是正比例函数,则a的值为 .
14.(3分)在平面直角坐标系中,将点A(2,﹣3)向右平移3个单位后得到点B,则点B的坐标为 .
15.(3分)若一个多边形的内角和等于其外角和的2倍,则它是 边形.
16.(3分)已知x,y满足方程组,则x﹣y的值是 .
17.(3分)如图,将?ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为 °.
18.(3分)如图,△ABC中,AB=AC=6,BC=8,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的周长是 .
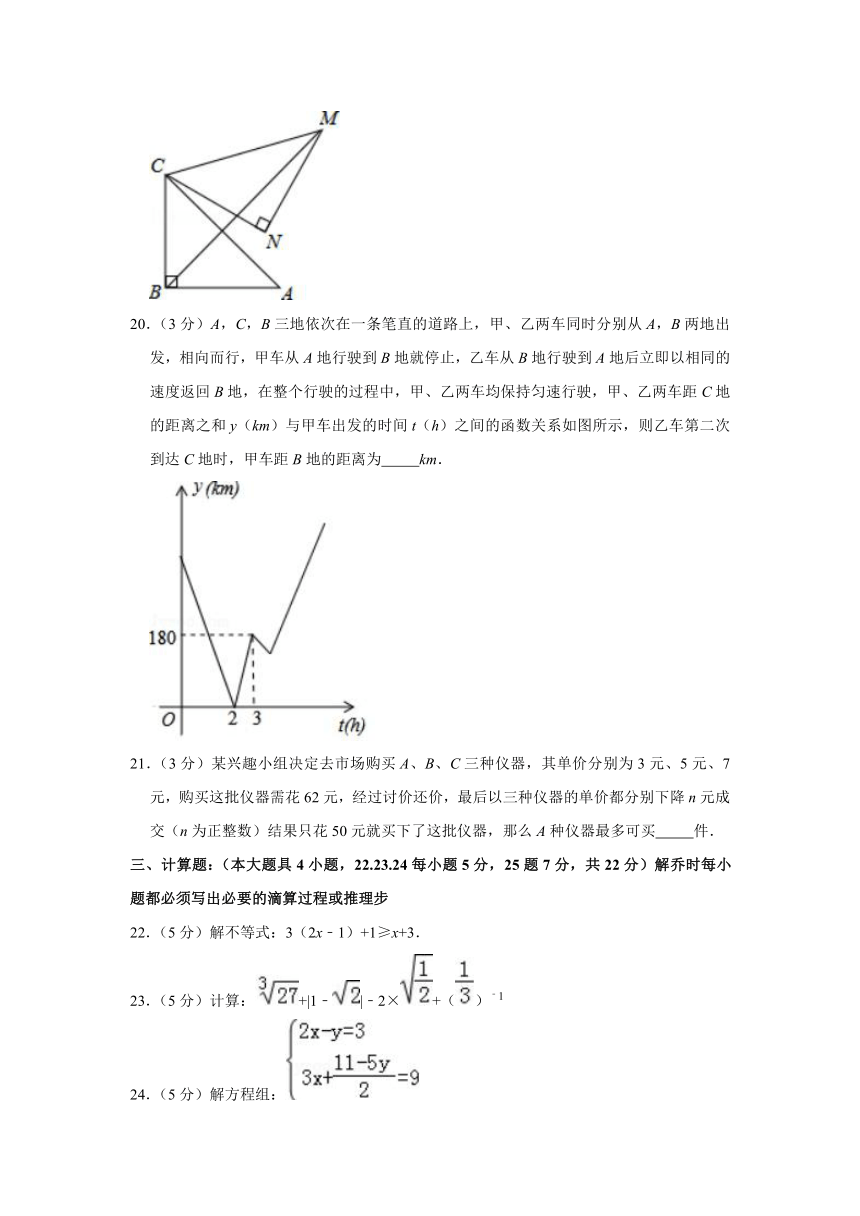
19.(3分)如图,在Rt△ABC中,∠ABC=90°,AB=BC=,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
20.(3分)A,C,B三地依次在一条笔直的道路上,甲、乙两车同时分别从A,B两地出发,相向而行,甲车从A地行驶到B地就停止,乙车从B地行驶到A地后立即以相同的速度返回B地,在整个行驶的过程中,甲、乙两车均保持匀速行驶,甲、乙两车距C地的距离之和y(km)与甲车出发的时间t(h)之间的函数关系如图所示,则乙车第二次到达C地时,甲车距B地的距离为 km.
21.(3分)某兴趣小组决定去市场购买A、B、C三种仪器,其单价分别为3元、5元、7元,购买这批仪器需花62元,经过讨价还价,最后以三种仪器的单价都分别下降n元成交(n为正整数)结果只花50元就买下了这批仪器,那么A种仪器最多可买 件.
三、计算题:(本大题具4小题,22.23.24每小题5分,25题7分,共22分)解乔时每小题都必须写出必要的滴算过程或推理步
22.(5分)解不等式:3(2x﹣1)+1≥x+3.
23.(5分)计算:+|1﹣|﹣2×+()﹣1
24.(5分)解方程组:
25.(7分)解不等式组并将解集在数轴上表示.
四、解答题:(本大题共6个小题,26、27、.28题每题7分,29,30每题10分,31题12分,共55分)解答时每小题必须给出必要的演算过程或推理步骤
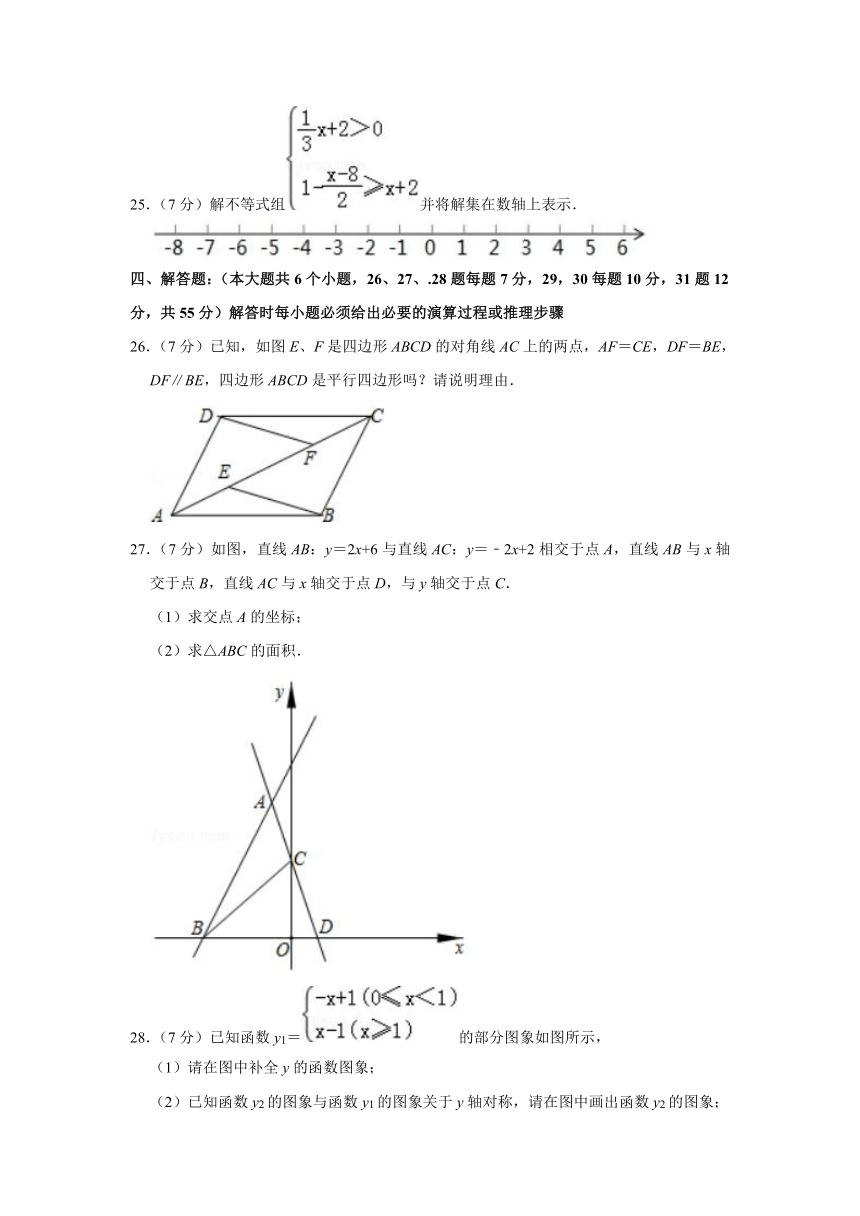
26.(7分)已知,如图E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE,四边形ABCD是平行四边形吗?请说明理由.
27.(7分)如图,直线AB:y=2x+6与直线AC:y=﹣2x+2相交于点A,直线AB与x轴交于点B,直线AC与x轴交于点D,与y轴交于点C.
(1)求交点A的坐标;
(2)求△ABC的面积.
28.(7分)已知函数y1=的部分图象如图所示,
(1)请在图中补全y的函数图象;
(2)已知函数y2的图象与函数y1的图象关于y轴对称,请在图中画出函数y2的图象;
(3)若直线y3=x+a与函数y1、y2的图象有且只有一个交点,则a的取值范围是 .
29.(10分)蓝莓果实中含有丰富的养成分,经常食用蓝莓制品,还可明显地增强视力,消除眼睛疲劳,某蓝莓种植生产基地产销两旺,当天采摘的蓝莓部分加工成蓝莓汁销售(按1斤蓝莓加工成1斤蓝莓汁计算),剩下的部分直接销售,且当天加工的蓝莓汁以及剩余的蓝莓都能在当天全部售出,3斤蓝梅与2斤蓝莓汁的售价是580元,4斤蓝莓与3斤蓝莓汁的售价是840元.已知基地佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤蓝莓或加工35斤蓝莓汁.
(1)请问购买1斤蓝莓多少元?购买1斤蓝莓汁多少元?
(2)设安排x名工人采摘蓝莓,剩下的工人加工蓝莓汁,基地应如何分配工人,才能使一天的销售额最大?并求出最大销售额.
30.(10分)已知:在?ABCD中,过点D作DE⊥BC交BC延长线于点E,且AD=DE,连接AC并延长交DE延长线于点F.
(1)如图1,若DF=3EF,AF=,求AD的长;
(2)如图2,作DG⊥AC于点G,作EM⊥AC于点M,连接DM,求证:AM+EM=2DG.
31.(12分)已知,在平面直角坐标系中,A(4,0),点B在第一象限,AB=4,且∠OAB=60°
(1)如图1:求直线AB的解析式;
(2)如图2,过点A作射线AM平分∠OAB,过B点作BC平行于x轴交射线AM于点C,将线段AB沿线段AC方向从点A向点C平移,记平移中的线段AB为A′B′,当△CA′B′为直角三角形时,在x轴上找一点P,使|PB′﹣PC|最大,请求出|PB′﹣PC|的最大值;
(3)如图3,在(2)的条件下,连接OC,将线段OC绕点O顺时针旋转角度α(0°≤α≤180°),记旋转中的线段OC为OC′,在旋转过程中,设线段OC′所在直线与直线BC交于点P,与直线AC交于点Q,△CPQ能否为等腰三角形?若能,请求出△CPQ的面积;若不能,请说明理由.
2018-2019学年重庆市南岸区南开(融侨)中学九年级(下)开学数学试卷
参考答案与试题解析
一、选择题1(本人题共12个小题,每小题4分,其4分)在每个小题的卜面,都给出了代为A,BC、D的四个答,其中只有个是正确的,请将每小的首案直接在答题卡中对应的方格中
1.【解答】解:∵(﹣2)×(﹣)=1,
∴﹣2的倒数是﹣.
故选:A.
2.【解答】解:A、不是中心对称图形,故本选项错误;
B、不是中心对称图形,故本选项错误;
C、不是中心对称图形,故本选项错误;
D、是中心对称图形,故本选项正确.
故选:D.
3.【解答】解:点M(﹣2,1)在第二象限.
故选:B.
4.【解答】解:A.∵32+42=52,∴△ABC是直角三角形;
B.∵52+42≠62,∴△ABC不是直角三角形;
C.∵62+82=102,∴△ABC是直角三角形;
D.∵122+42=132,∴△ABC是直角三角形;
故选:B.
5.【解答】解:A、两直线平行,同位角相等,故错误,是假命题;
B、对顶角相等,但相等的角不一定是对顶角,故错误,是假命题;
C、邻补角一定互补,正确,是真命题;
D、过一点有且只有一条直线与已知直线垂直,故错误,是假命题,
故选:C.
6.【解答】解:A.若a>b,不等式两边同时加上3得:a+3>b+3,即A项正确,
B.若﹣a>﹣b,不等式两边同时乘以﹣1得:a<b,即B项正确,
C.若﹣x<y,不等式两边同时乘以﹣2得:x>﹣2y,即C项正确,
D.若﹣2x>a,不等式两边同时乘以﹣得:x,即D项错误,
故选:D.
7.【解答】解:∵?ABCD的周长是22,△ABC的周长是17,
∴AB+BC=11,AB+BC+AC=17,
∴AC=17﹣11=6,
故选:B.
8.【解答】解:(2﹣)?
=2﹣2
=﹣2,
∵4<<5,
∴2<﹣2<3,
故选:B.
9.【解答】解:根据题意得:x+2≥0且x﹣1≠0,
解得:x≥﹣2且x≠1.
故选:C.
10.【解答】解:当x>﹣1时,x+b>kx﹣1,
即不等式x+b>kx﹣1的解集为x>﹣1.
故选:A.
11.【解答】解:图形①中有3+1+1=5个小正方形,图形②中共有5+3+1+1=10个小正方形,图形③中共有7+5+3+1+1=17个小正方形,
图形⑩中小正方形的个数是31+19+17+15+13+11+9+7+5+3+1+1=22
故选:D.
12.【解答】解:解方程组得,
∵方程组的解为正整数,
∴,
∴k=4,6;
解不等式组得,,
∵不等式组有且仅有四个整数解,
∴1<≤2,
∴3<k≤6,
∴k=4,5,6,
∴所有满足条件的k的和=4+6=10,
故选:C.
二、填空题,(本大题共9个小题,每小3分,共27分)
13.【解答】解:∵y=xa﹣1是正比例函数,
∴a﹣1=1,
解得:a=2.
故答案为:2.
14.【解答】解:由题中的平移规律可知:点B的横坐标为2+3=5;
纵坐标为﹣3;
∴点B的坐标为(5,﹣3).
故答案为:(5,﹣3).
15.【解答】解:设这个多边形是n边形,根据题意得,
(n﹣2)?180°=2×360°,
解得n=6.
故答案为:六.
16.【解答】解:,
②﹣①得:x﹣y=﹣1.
故答案为:﹣1.
17.【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠B′AC,
∴∠BAC=∠ACD=∠B′AC=∠1=22°,
∴∠B=180°﹣∠2﹣∠BAC=180°﹣44°﹣22°=114°,
故答案为:114.
18.【解答】解:如右图所示,
∵AB=AC,AE平分∠BAC交BC于点E,
∴BE=CE=4,
又∵D为AB的中点,
∴DE是△BAC的中位线,
∴DE=AC=3,
∴△BDE的周长=3+3+4=10.
故答案是10.
19.【解答】解:如图,连接AM,
由题意得:CA=CM,∠ACM=60°,
∴△ACM为等边三角形,
∴AM=CM,∠MAC=∠MCA=∠AMC=60°;
∵∠ABC=90°,AB=BC=,
∴AC=2=CM=2,
∵AB=BC,CM=AM,
∴BM垂直平分AC,
∴BO=AC=1,OM=CM?sin60°=,
∴BM=BO+OM=1+,
故答案为:1+.
20.【解答】解:由题意得:A地到C地甲走了2个小时,乙走了1个小时,
设甲的速度为akm/h,则乙的速度为2akm/h,
2a+3a﹣2a=180,
a=60,
则A、B两地的距离为:2a+4a=6a=360,
A、C两地的距离为:2×60=120,
乙第二次到达C地的时间为:=4h,
360﹣4×60=120(千米),
答:则乙车第二次到达C地时,甲车距B地的距离为120km.
故答案为:120.
21.【解答】解:设分别购买A,B,C三种仪器为x,y,z台
则有:
解得:(2x+y+31)?n=42
∴n=
又∵n为正整数 且(2x+y+31)也为正整数
∴2x+y+31=42
∴x=
当y=1时,x取最大值
x=5
故A种仪器最多可买5台.
三、计算题:(本大题具4小题,22.23.24每小题5分,25题7分,共22分)解乔时每小题都必须写出必要的滴算过程或推理步
22.【解答】解:3(2x﹣1)+1≥x+3
去分母,得
6x﹣3+1≥x+3
移项及合并同类项,得
5x≥5
系数化为1,得
x≥1,
∴原不等式组的解集为x≥1.
23.【解答】解:原式=3+﹣1﹣+3
=5.
24.【解答】解:,
由①可得:y=2x﹣3③,
把③代入②可得:,
解得:x=2,
把x=2代入③得:y=1,
所以方程组的解为:.
25.【解答】解:,
解①得x>﹣6,
解②得x≤2,
所以不等式组的解集为﹣6<x≤2,
用数轴表示为
.
四、解答题:(本大题共6个小题,26、27、.28题每题7分,29,30每题10分,31题12分,共55分)解答时每小题必须给出必要的演算过程或推理步骤
26.【解答】解:结论:四边形ABCD是平行四边形,
证明:∵DF∥BE,
∴∠AFD=∠CEB,
又∵AF=CE DF=BE,
∴△AFD≌△CEB(SAS),
∴AD=CB,∠DAF=∠BCE,
∴AD∥CB,
∴四边形ABCD是平行四边形.
27.【解答】解:(1)联立直线AB,AC的解析式成方程组,得:,
解得:,
∴交点A的坐标为(﹣1,4).
(2)设直线AB与y轴交于点E,如图所示.
当x=0时,y=2x+6=6,y=﹣2x+2=2,
∴点E的坐标为(0,6),点C的坐标为(0,2),
∴OE=6,OC=2,CE=4.
当y=0时,2x+6=0,
解得:x=﹣3,
∴点B的坐标为(﹣3,0),OB=3.
∴S△ABC=S△BOE﹣S△BOC﹣S△ACE,
=×3×6﹣×3×2﹣×4×1,
=4.
28.【解答】解:(1)函数y1的图象如图所示,
(2)函数y2的图象如图所示;
(3)∵直线y3=x+a与函数y1、y2的图象有且只有一个交点,
∴a的取值范围为:a>1或﹣1<a<1.
故答案为:a>1或﹣1<a<1.
29.【解答】解:(1)设购买1斤蓝莓x元,购买1斤蓝莓汁y元,
根据题意得:,
解得:,
则购买1斤蓝莓60元,购买1斤蓝莓汁200元;
(2)设安排x名工人采摘蓝莓,剩下的(20﹣x)名工人加工蓝莓汁,销售额为y元,
根据题意得:y=70x×60+35×(20﹣x)×200=4200x+14000﹣7000x=﹣2800x+14000,
∵﹣2800<0,∴y与x的一次函数为减函数,
当x最小,即x=0时,y取得最大值,最大值为14000,
则20名工人加工蓝莓汁,才能使一天的销售额最大,最大销售额为14000元.
30.【解答】解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∵DE⊥BC,
∴DE⊥AD,
∵DF=3EF,
∴DE=2EF,
∵AD=DE,
∴AD=2EF,
在Rt△ADF中,∵AD2+DF2=AF2,
∴(2EF)2+(3EF)2=13,
∴EF=,
∴AD=2EF=;
(2)如图2,过E作EN⊥DG于N,
∵DG⊥AC,EM⊥AC,
∴四边形GMEN是矩形,
∴GM=EN,GN=EM,
∵∠DAG+∠ADG=∠ADG+∠NDE=90°,
∴∠DAG=∠EDN,
在△ADG与△EDN中,,
∴△ADG≌△EDN(AAS),
∴DG=NE,DN=AG,
∴GM=DG,AG+EM=DG=GM,
∴AM+EM=AG+GM+EM=2DG.
31.【解答】解:(1)如图1,过点B作BH⊥OA于H,
在Rt△ABH中,AB=4,∠OAB=60°,
∴∠ABH=30°,
∴AH=2,BH=,
∴OH=OA﹣AH=2,
∴B(2,2),
设直线AB的解析式为y=kx+b,
则,解得
∴直线AB的解析式为y=x+4,
(2)由题意,A'B'∥AB,A'B'=AB=4
∴∠CA'B'=∠CAB=30°,
∵△CA′B′为直角三角形,
∴①如图2,∠A'B'C=90°,
∵A'B'=4,
∴B'C=
由三角形的三边关系得,|PB'﹣PC|<B'C,
∴当点P,C,B'在同一条直线上时,|PB'﹣PC|最大,最大值为B'C=
②如图3,∠A'CB=90°,同①的方法得,|PB'﹣PC|的最大值为2,
而>2,
即:|PB'﹣PC|的最大值为.
(3)由题意,可得四边形OABC为菱形,∠OCB=60°,∠BCA=30°,
∵△CPQ为等腰三角形,
①如图4,当CP=CQ时,
∠CPQ=∠CQP=(180°﹣∠ACB)=75°,
∴∠POC=180°﹣∠BCO﹣∠OPC=45°,
作PH⊥OC于H,QN⊥BC于N,
设CH=x,则PH=OH=,
∵OC=AB=4,
∴,
∴,
∴PC=CQ=2x=,QN=CQ=,
∴△CPQ面积=.
②如图5,当QC=QP时,
∠CPQ=∠PCQ=30°,
∵∠PCO=60°,
∴∠POC=180°﹣∠CPQ﹣∠PCO=90°,
∵OC=4,
∴QP=QC=,
∴△CPQ面积=
③如图6,当CP=CQ时,作PH⊥OC于H,QN⊥BC于N,
∴∠CPQ=∠CQP=15°,
∵∠PCH=∠BCO=60°,
∴∠OCP=45°,
设CH=x,则PH=OH=,
∴
∴,
同理可得△CPQ面积为.
一、选择题1(本人题共12个小题,每小题4分,其4分)在每个小题的卜面,都给出了代为A,BC、D的四个答,其中只有个是正确的,请将每小的首案直接在答题卡中对应的方格中
1.(4分)﹣2的倒数是( )
A.﹣ B. C.2 D.﹣2
2.(4分)下列电视台图标中,属于中心对称图形的是( )
A. B.
C. D.
3.(4分)在平面直角坐标系中,点M(﹣2,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(4分)△ABC三边长分别为a、b、c,则下列条件不能判断△ABC是直角三角形的是( )
A.a=3,b=4,c=5 B.a=4,b=5,c=6
C.a=6,b=8,c=10 D.a=5,b=12,c=13
5.(4分)下列命题中,是真命题的是( )
A.同位角相等
B.相等的角是对顶角
C.邻补角一定互补
D.有且只有一条直线与已知直线垂直
6.(4分)下列不等式的变形不正确的是( )
A.若a>b,则a+3>b+3 B.若﹣a>﹣b则a<b:
C.若﹣x<y,则x>﹣2y D.若﹣2x>a,则x>﹣a
7.(4分)已知?ABCD的周长是22,△ABC的周长是17,则AC的长为( )
A.5 B.6 C.7 D.8
8.(4分)估计(2﹣)?的值应在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
9.(4分)在关于x的函数y=+(x﹣1)0中,自变量x的取值范图是( )
A.x≥﹣2 B.x≥﹣2且x≠0 C.x≥﹣2且x≠1 D.x≥1
10.(4分)如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是( )
A. B.
C. D.
11.(4分)观察下列一组图形,图形①中有5个小正方形,图形②中共有10个小正方形,图形③中共有17个小正方形,…,按此规律,图形⑩中小正方形的个数是( )
A.100个 B.101个 C.121个 D.122个
12.(4分)已知整数k使得关于x、y的二元一次方程组的解为正整数,且关于x的不等式组有且仅有四个整数解,则所有满足条件的k的和为( )
A.4 B.9 C.10 D.12
二、填空题,(本大题共9个小题,每小3分,共27分)
13.(3分)已知y=xa﹣1是正比例函数,则a的值为 .
14.(3分)在平面直角坐标系中,将点A(2,﹣3)向右平移3个单位后得到点B,则点B的坐标为 .
15.(3分)若一个多边形的内角和等于其外角和的2倍,则它是 边形.
16.(3分)已知x,y满足方程组,则x﹣y的值是 .
17.(3分)如图,将?ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为 °.
18.(3分)如图,△ABC中,AB=AC=6,BC=8,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的周长是 .
19.(3分)如图,在Rt△ABC中,∠ABC=90°,AB=BC=,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
20.(3分)A,C,B三地依次在一条笔直的道路上,甲、乙两车同时分别从A,B两地出发,相向而行,甲车从A地行驶到B地就停止,乙车从B地行驶到A地后立即以相同的速度返回B地,在整个行驶的过程中,甲、乙两车均保持匀速行驶,甲、乙两车距C地的距离之和y(km)与甲车出发的时间t(h)之间的函数关系如图所示,则乙车第二次到达C地时,甲车距B地的距离为 km.
21.(3分)某兴趣小组决定去市场购买A、B、C三种仪器,其单价分别为3元、5元、7元,购买这批仪器需花62元,经过讨价还价,最后以三种仪器的单价都分别下降n元成交(n为正整数)结果只花50元就买下了这批仪器,那么A种仪器最多可买 件.
三、计算题:(本大题具4小题,22.23.24每小题5分,25题7分,共22分)解乔时每小题都必须写出必要的滴算过程或推理步
22.(5分)解不等式:3(2x﹣1)+1≥x+3.
23.(5分)计算:+|1﹣|﹣2×+()﹣1
24.(5分)解方程组:
25.(7分)解不等式组并将解集在数轴上表示.
四、解答题:(本大题共6个小题,26、27、.28题每题7分,29,30每题10分,31题12分,共55分)解答时每小题必须给出必要的演算过程或推理步骤
26.(7分)已知,如图E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE,四边形ABCD是平行四边形吗?请说明理由.
27.(7分)如图,直线AB:y=2x+6与直线AC:y=﹣2x+2相交于点A,直线AB与x轴交于点B,直线AC与x轴交于点D,与y轴交于点C.
(1)求交点A的坐标;
(2)求△ABC的面积.
28.(7分)已知函数y1=的部分图象如图所示,
(1)请在图中补全y的函数图象;
(2)已知函数y2的图象与函数y1的图象关于y轴对称,请在图中画出函数y2的图象;
(3)若直线y3=x+a与函数y1、y2的图象有且只有一个交点,则a的取值范围是 .
29.(10分)蓝莓果实中含有丰富的养成分,经常食用蓝莓制品,还可明显地增强视力,消除眼睛疲劳,某蓝莓种植生产基地产销两旺,当天采摘的蓝莓部分加工成蓝莓汁销售(按1斤蓝莓加工成1斤蓝莓汁计算),剩下的部分直接销售,且当天加工的蓝莓汁以及剩余的蓝莓都能在当天全部售出,3斤蓝梅与2斤蓝莓汁的售价是580元,4斤蓝莓与3斤蓝莓汁的售价是840元.已知基地佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤蓝莓或加工35斤蓝莓汁.
(1)请问购买1斤蓝莓多少元?购买1斤蓝莓汁多少元?
(2)设安排x名工人采摘蓝莓,剩下的工人加工蓝莓汁,基地应如何分配工人,才能使一天的销售额最大?并求出最大销售额.
30.(10分)已知:在?ABCD中,过点D作DE⊥BC交BC延长线于点E,且AD=DE,连接AC并延长交DE延长线于点F.
(1)如图1,若DF=3EF,AF=,求AD的长;
(2)如图2,作DG⊥AC于点G,作EM⊥AC于点M,连接DM,求证:AM+EM=2DG.
31.(12分)已知,在平面直角坐标系中,A(4,0),点B在第一象限,AB=4,且∠OAB=60°
(1)如图1:求直线AB的解析式;
(2)如图2,过点A作射线AM平分∠OAB,过B点作BC平行于x轴交射线AM于点C,将线段AB沿线段AC方向从点A向点C平移,记平移中的线段AB为A′B′,当△CA′B′为直角三角形时,在x轴上找一点P,使|PB′﹣PC|最大,请求出|PB′﹣PC|的最大值;
(3)如图3,在(2)的条件下,连接OC,将线段OC绕点O顺时针旋转角度α(0°≤α≤180°),记旋转中的线段OC为OC′,在旋转过程中,设线段OC′所在直线与直线BC交于点P,与直线AC交于点Q,△CPQ能否为等腰三角形?若能,请求出△CPQ的面积;若不能,请说明理由.
2018-2019学年重庆市南岸区南开(融侨)中学九年级(下)开学数学试卷
参考答案与试题解析
一、选择题1(本人题共12个小题,每小题4分,其4分)在每个小题的卜面,都给出了代为A,BC、D的四个答,其中只有个是正确的,请将每小的首案直接在答题卡中对应的方格中
1.【解答】解:∵(﹣2)×(﹣)=1,
∴﹣2的倒数是﹣.
故选:A.
2.【解答】解:A、不是中心对称图形,故本选项错误;
B、不是中心对称图形,故本选项错误;
C、不是中心对称图形,故本选项错误;
D、是中心对称图形,故本选项正确.
故选:D.
3.【解答】解:点M(﹣2,1)在第二象限.
故选:B.
4.【解答】解:A.∵32+42=52,∴△ABC是直角三角形;
B.∵52+42≠62,∴△ABC不是直角三角形;
C.∵62+82=102,∴△ABC是直角三角形;
D.∵122+42=132,∴△ABC是直角三角形;
故选:B.
5.【解答】解:A、两直线平行,同位角相等,故错误,是假命题;
B、对顶角相等,但相等的角不一定是对顶角,故错误,是假命题;
C、邻补角一定互补,正确,是真命题;
D、过一点有且只有一条直线与已知直线垂直,故错误,是假命题,
故选:C.
6.【解答】解:A.若a>b,不等式两边同时加上3得:a+3>b+3,即A项正确,
B.若﹣a>﹣b,不等式两边同时乘以﹣1得:a<b,即B项正确,
C.若﹣x<y,不等式两边同时乘以﹣2得:x>﹣2y,即C项正确,
D.若﹣2x>a,不等式两边同时乘以﹣得:x,即D项错误,
故选:D.
7.【解答】解:∵?ABCD的周长是22,△ABC的周长是17,
∴AB+BC=11,AB+BC+AC=17,
∴AC=17﹣11=6,
故选:B.
8.【解答】解:(2﹣)?
=2﹣2
=﹣2,
∵4<<5,
∴2<﹣2<3,
故选:B.
9.【解答】解:根据题意得:x+2≥0且x﹣1≠0,
解得:x≥﹣2且x≠1.
故选:C.
10.【解答】解:当x>﹣1时,x+b>kx﹣1,
即不等式x+b>kx﹣1的解集为x>﹣1.
故选:A.
11.【解答】解:图形①中有3+1+1=5个小正方形,图形②中共有5+3+1+1=10个小正方形,图形③中共有7+5+3+1+1=17个小正方形,
图形⑩中小正方形的个数是31+19+17+15+13+11+9+7+5+3+1+1=22
故选:D.
12.【解答】解:解方程组得,
∵方程组的解为正整数,
∴,
∴k=4,6;
解不等式组得,,
∵不等式组有且仅有四个整数解,
∴1<≤2,
∴3<k≤6,
∴k=4,5,6,
∴所有满足条件的k的和=4+6=10,
故选:C.
二、填空题,(本大题共9个小题,每小3分,共27分)
13.【解答】解:∵y=xa﹣1是正比例函数,
∴a﹣1=1,
解得:a=2.
故答案为:2.
14.【解答】解:由题中的平移规律可知:点B的横坐标为2+3=5;
纵坐标为﹣3;
∴点B的坐标为(5,﹣3).
故答案为:(5,﹣3).
15.【解答】解:设这个多边形是n边形,根据题意得,
(n﹣2)?180°=2×360°,
解得n=6.
故答案为:六.
16.【解答】解:,
②﹣①得:x﹣y=﹣1.
故答案为:﹣1.
17.【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠B′AC,
∴∠BAC=∠ACD=∠B′AC=∠1=22°,
∴∠B=180°﹣∠2﹣∠BAC=180°﹣44°﹣22°=114°,
故答案为:114.
18.【解答】解:如右图所示,
∵AB=AC,AE平分∠BAC交BC于点E,
∴BE=CE=4,
又∵D为AB的中点,
∴DE是△BAC的中位线,
∴DE=AC=3,
∴△BDE的周长=3+3+4=10.
故答案是10.
19.【解答】解:如图,连接AM,
由题意得:CA=CM,∠ACM=60°,
∴△ACM为等边三角形,
∴AM=CM,∠MAC=∠MCA=∠AMC=60°;
∵∠ABC=90°,AB=BC=,
∴AC=2=CM=2,
∵AB=BC,CM=AM,
∴BM垂直平分AC,
∴BO=AC=1,OM=CM?sin60°=,
∴BM=BO+OM=1+,
故答案为:1+.
20.【解答】解:由题意得:A地到C地甲走了2个小时,乙走了1个小时,
设甲的速度为akm/h,则乙的速度为2akm/h,
2a+3a﹣2a=180,
a=60,
则A、B两地的距离为:2a+4a=6a=360,
A、C两地的距离为:2×60=120,
乙第二次到达C地的时间为:=4h,
360﹣4×60=120(千米),
答:则乙车第二次到达C地时,甲车距B地的距离为120km.
故答案为:120.
21.【解答】解:设分别购买A,B,C三种仪器为x,y,z台
则有:
解得:(2x+y+31)?n=42
∴n=
又∵n为正整数 且(2x+y+31)也为正整数
∴2x+y+31=42
∴x=
当y=1时,x取最大值
x=5
故A种仪器最多可买5台.
三、计算题:(本大题具4小题,22.23.24每小题5分,25题7分,共22分)解乔时每小题都必须写出必要的滴算过程或推理步
22.【解答】解:3(2x﹣1)+1≥x+3
去分母,得
6x﹣3+1≥x+3
移项及合并同类项,得
5x≥5
系数化为1,得
x≥1,
∴原不等式组的解集为x≥1.
23.【解答】解:原式=3+﹣1﹣+3
=5.
24.【解答】解:,
由①可得:y=2x﹣3③,
把③代入②可得:,
解得:x=2,
把x=2代入③得:y=1,
所以方程组的解为:.
25.【解答】解:,
解①得x>﹣6,
解②得x≤2,
所以不等式组的解集为﹣6<x≤2,
用数轴表示为
.
四、解答题:(本大题共6个小题,26、27、.28题每题7分,29,30每题10分,31题12分,共55分)解答时每小题必须给出必要的演算过程或推理步骤
26.【解答】解:结论:四边形ABCD是平行四边形,
证明:∵DF∥BE,
∴∠AFD=∠CEB,
又∵AF=CE DF=BE,
∴△AFD≌△CEB(SAS),
∴AD=CB,∠DAF=∠BCE,
∴AD∥CB,
∴四边形ABCD是平行四边形.
27.【解答】解:(1)联立直线AB,AC的解析式成方程组,得:,
解得:,
∴交点A的坐标为(﹣1,4).
(2)设直线AB与y轴交于点E,如图所示.
当x=0时,y=2x+6=6,y=﹣2x+2=2,
∴点E的坐标为(0,6),点C的坐标为(0,2),
∴OE=6,OC=2,CE=4.
当y=0时,2x+6=0,
解得:x=﹣3,
∴点B的坐标为(﹣3,0),OB=3.
∴S△ABC=S△BOE﹣S△BOC﹣S△ACE,
=×3×6﹣×3×2﹣×4×1,
=4.
28.【解答】解:(1)函数y1的图象如图所示,
(2)函数y2的图象如图所示;
(3)∵直线y3=x+a与函数y1、y2的图象有且只有一个交点,
∴a的取值范围为:a>1或﹣1<a<1.
故答案为:a>1或﹣1<a<1.
29.【解答】解:(1)设购买1斤蓝莓x元,购买1斤蓝莓汁y元,
根据题意得:,
解得:,
则购买1斤蓝莓60元,购买1斤蓝莓汁200元;
(2)设安排x名工人采摘蓝莓,剩下的(20﹣x)名工人加工蓝莓汁,销售额为y元,
根据题意得:y=70x×60+35×(20﹣x)×200=4200x+14000﹣7000x=﹣2800x+14000,
∵﹣2800<0,∴y与x的一次函数为减函数,
当x最小,即x=0时,y取得最大值,最大值为14000,
则20名工人加工蓝莓汁,才能使一天的销售额最大,最大销售额为14000元.
30.【解答】解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∵DE⊥BC,
∴DE⊥AD,
∵DF=3EF,
∴DE=2EF,
∵AD=DE,
∴AD=2EF,
在Rt△ADF中,∵AD2+DF2=AF2,
∴(2EF)2+(3EF)2=13,
∴EF=,
∴AD=2EF=;
(2)如图2,过E作EN⊥DG于N,
∵DG⊥AC,EM⊥AC,
∴四边形GMEN是矩形,
∴GM=EN,GN=EM,
∵∠DAG+∠ADG=∠ADG+∠NDE=90°,
∴∠DAG=∠EDN,
在△ADG与△EDN中,,
∴△ADG≌△EDN(AAS),
∴DG=NE,DN=AG,
∴GM=DG,AG+EM=DG=GM,
∴AM+EM=AG+GM+EM=2DG.
31.【解答】解:(1)如图1,过点B作BH⊥OA于H,
在Rt△ABH中,AB=4,∠OAB=60°,
∴∠ABH=30°,
∴AH=2,BH=,
∴OH=OA﹣AH=2,
∴B(2,2),
设直线AB的解析式为y=kx+b,
则,解得
∴直线AB的解析式为y=x+4,
(2)由题意,A'B'∥AB,A'B'=AB=4
∴∠CA'B'=∠CAB=30°,
∵△CA′B′为直角三角形,
∴①如图2,∠A'B'C=90°,
∵A'B'=4,
∴B'C=
由三角形的三边关系得,|PB'﹣PC|<B'C,
∴当点P,C,B'在同一条直线上时,|PB'﹣PC|最大,最大值为B'C=
②如图3,∠A'CB=90°,同①的方法得,|PB'﹣PC|的最大值为2,
而>2,
即:|PB'﹣PC|的最大值为.
(3)由题意,可得四边形OABC为菱形,∠OCB=60°,∠BCA=30°,
∵△CPQ为等腰三角形,
①如图4,当CP=CQ时,
∠CPQ=∠CQP=(180°﹣∠ACB)=75°,
∴∠POC=180°﹣∠BCO﹣∠OPC=45°,
作PH⊥OC于H,QN⊥BC于N,
设CH=x,则PH=OH=,
∵OC=AB=4,
∴,
∴,
∴PC=CQ=2x=,QN=CQ=,
∴△CPQ面积=.
②如图5,当QC=QP时,
∠CPQ=∠PCQ=30°,
∵∠PCO=60°,
∴∠POC=180°﹣∠CPQ﹣∠PCO=90°,
∵OC=4,
∴QP=QC=,
∴△CPQ面积=
③如图6,当CP=CQ时,作PH⊥OC于H,QN⊥BC于N,
∴∠CPQ=∠CQP=15°,
∵∠PCH=∠BCO=60°,
∴∠OCP=45°,
设CH=x,则PH=OH=,
∴
∴,
同理可得△CPQ面积为.
同课章节目录
