人教版九年级下册 26.2.2反比例函数在实际中的应用 共32张PPT
文档属性
| 名称 | 人教版九年级下册 26.2.2反比例函数在实际中的应用 共32张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-20 09:04:58 | ||
图片预览






文档简介
课件32张PPT。天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是如钻石般耀眼
老师的幸福是因为认识了你们
愿你们努力进取,永不言败致我亲爱的同学们1.什么叫反比例函数?
2.反比例函数通常有哪三种形式(k≠0):
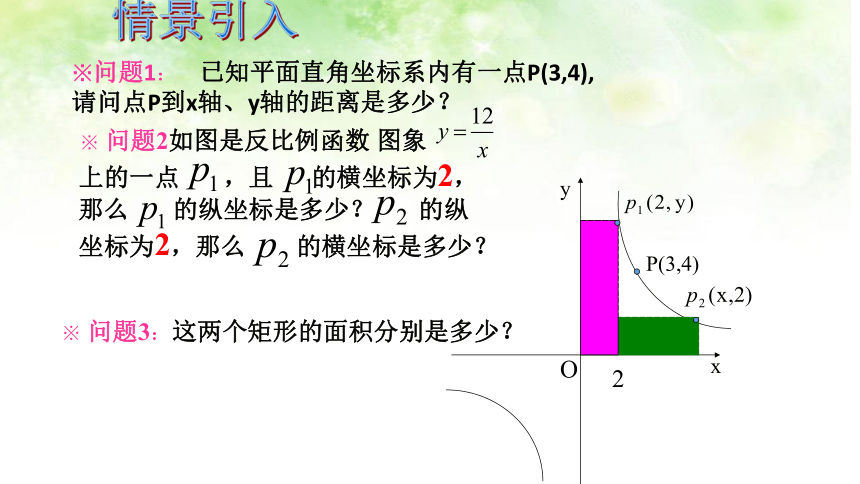
复习提问※问题1: 已知平面直角坐标系内有一点P(3,4),
请问点P到x轴、y轴的距离是多少? xyO
※ 问题3:这两个矩形的面积分别是多少?2情景引入反比例函数中的面积问题学
习
目
标1、会推导反比例函数与三角形、矩形面积
关系的性质;灵活运用性质解决与面积有关
的问题。
2、引导学生自主探索,合作研讨,培养观
察、分析、归纳问题的能力,体会数形结合
的思想。
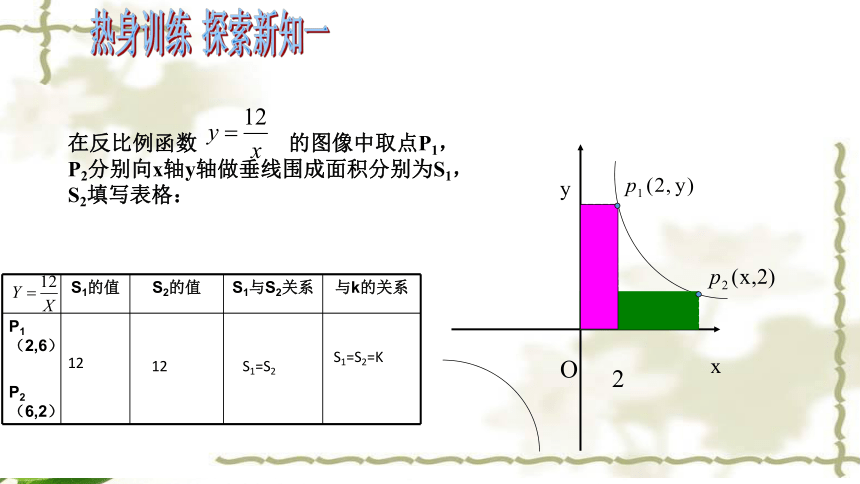
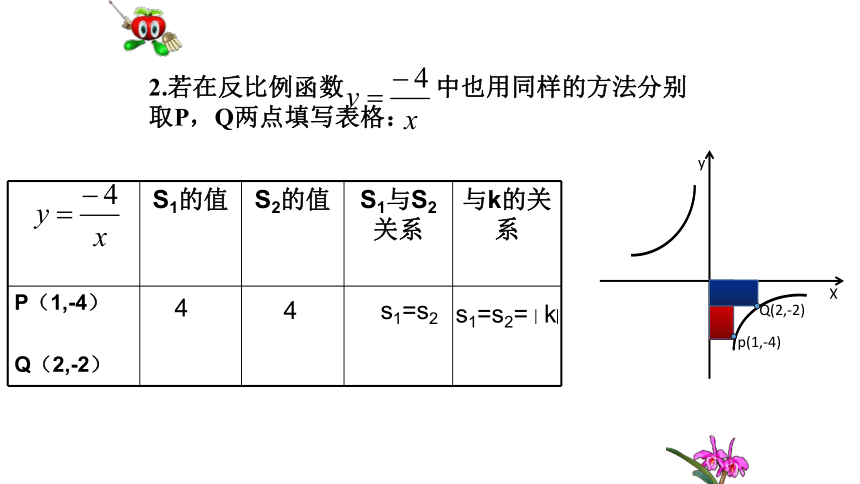
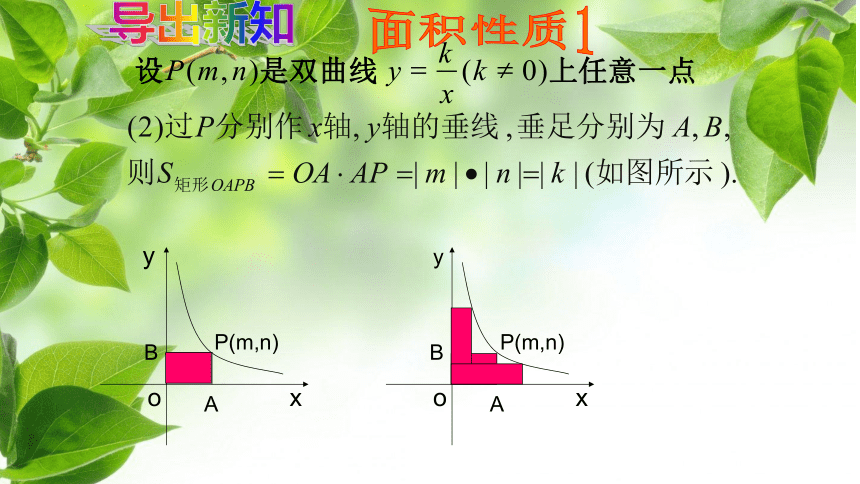
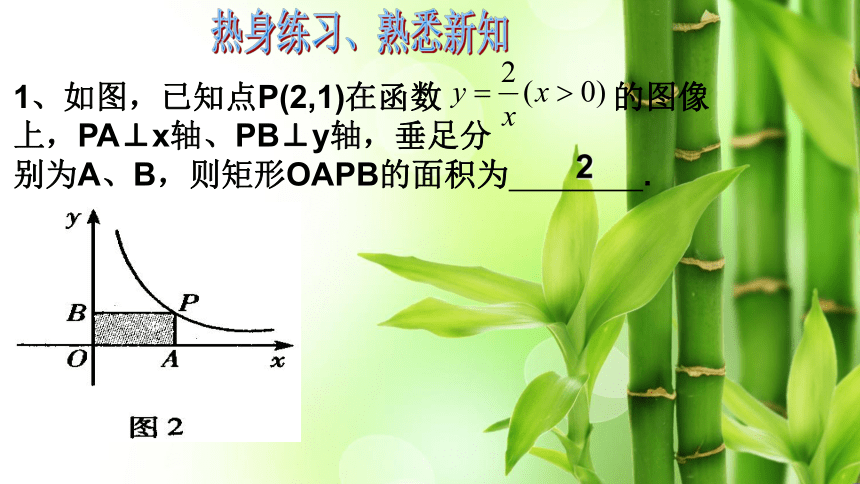
xyO2在反比例函数 的图像中取点P1,P2分别向x轴y轴做垂线围成面积分别为S1,S2填写表格:热身训练 探索新知一1212S1=S2S1=S2=K2.若在反比例函数 中也用同样的方法分别取P,Q两点填写表格:44s1=s2s1=s2=︱k︳Q(2,-2)p(1,-4)Xy面积性质1导出新知1、如图,已知点P(2,1)在函数 的图像上,PA⊥x轴、PB⊥y轴,垂足分
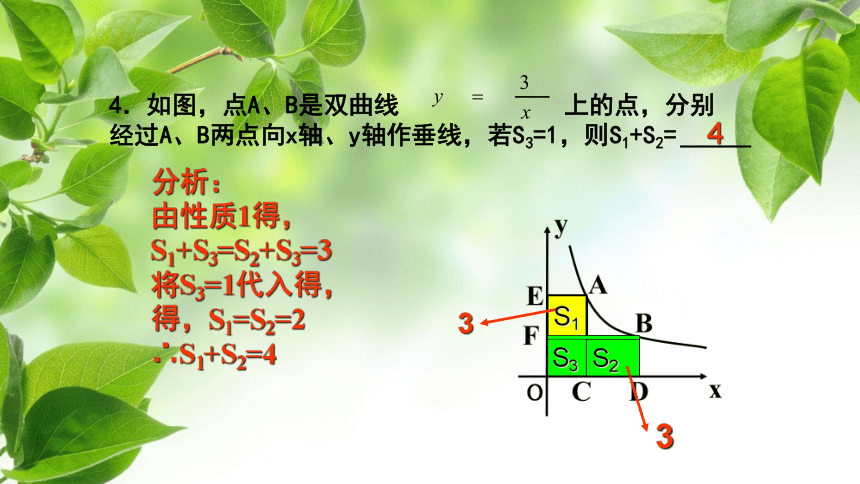
别为A、B,则矩形OAPB的面积为 . 2热身练习、熟悉新知 2、 如图,点p是反比例函数 图像上一点,PD⊥X轴,PC⊥Y轴,则矩形PCOD的面积为 .xyOCDP8热身练习、熟悉新知3、如图,点P是反比例函数 图象上的一点,过P分别向x轴,y轴引垂线,垂足分别为A,C,阴影部分的面积为3,则这个反比例函数的解析式是 热身练习、熟悉新知4.如图,点A、B是双曲线 上的点,分别经过A、B两点向x轴、y轴作垂线,若S3=1,则S1+S2= 33S1S2S34分析:
由性质1得,
S1+S3=S2+S3=3
将S3=1代入得,
得,S1=S2=2
∴S1+S2=41、如图①,点P(2,1)是反比例函数 图象上的一点,PD⊥x轴于D,则△ POD的面积为1图①P(2,1)DoyxDo
S △ OPD= 热身训练、探索新知二1、如图①,点P(m,n)是反比例函数 图象上的任意一点,PD⊥x轴于D,则△ POD的面积为1图①P(m,n)oyxDo分析:
S △ OPD= 热身练习、熟悉新知则垂足为轴的垂线作过上任意一点是双曲线设,,)0(),(AxPkxynmP1=k导出新知请你思考面积性质21、如图,点P是反比例函数 图象上的任一点,过点P作PD⊥Y轴于D,则△POD的面积为 .D2热身练习、熟悉新知2、如图:点A在双曲线 上,AB⊥x轴于B,且△ AOB的面积S △ AOB=2,则k= -43、如图,在x轴上点P的右侧有一点D,过点D作x轴的垂线交双曲线 于点B,连结BO交AP于C,设△AOP的面积为S1,梯形BCPD面积为S2,则S1与S2的大小关系是S1 S2 。(选填“>”“<”或“=”)=4、如图,A、C是函数 的图象上的任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记Rt △ AOB的面积为S1,Rt △ OCD的面积为S2,则( )
A.S1>S2
B.S1< S2
C.S1=S2
D.S1和S2的大小关系不确定oA(m,n)CBDCA.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3 提高训练A1、如图,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为2,则这个反比
例函数的解析式为 . 点评:将△ABO通过“等积变换”同底等高变为△ABP拓展提升2、如图,过反比例函数 图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E, △ AOE与梯形ECDB的面积分别为 S1 、S2,比较它们的大小,可得 ( )
A.S1>S2 B.S1=S2
C.S1< S2 D.S1和S2的大小关系不确定ByxACBODE链接中考链接中考链接中考课堂小结通过这节课的学习,你有什么收获?⑴ 反比例函数图象上任意一点“对应的直角三角形”面积S1与k值有什么关系?
⑵ 反比例函数图象上任意一点“对应的矩形”面积S2与k值有什么关系?
必做题:课后小卷1--10
选做题:11、12
预习第27章第一节相似图形作业布置谢谢指导再见
森林的幸福是披一身绿
阳光的幸福是如钻石般耀眼
老师的幸福是因为认识了你们
愿你们努力进取,永不言败致我亲爱的同学们1.什么叫反比例函数?
2.反比例函数通常有哪三种形式(k≠0):
复习提问※问题1: 已知平面直角坐标系内有一点P(3,4),
请问点P到x轴、y轴的距离是多少? xyO
※ 问题3:这两个矩形的面积分别是多少?2情景引入反比例函数中的面积问题学
习
目
标1、会推导反比例函数与三角形、矩形面积
关系的性质;灵活运用性质解决与面积有关
的问题。
2、引导学生自主探索,合作研讨,培养观
察、分析、归纳问题的能力,体会数形结合
的思想。
xyO2在反比例函数 的图像中取点P1,P2分别向x轴y轴做垂线围成面积分别为S1,S2填写表格:热身训练 探索新知一1212S1=S2S1=S2=K2.若在反比例函数 中也用同样的方法分别取P,Q两点填写表格:44s1=s2s1=s2=︱k︳Q(2,-2)p(1,-4)Xy面积性质1导出新知1、如图,已知点P(2,1)在函数 的图像上,PA⊥x轴、PB⊥y轴,垂足分
别为A、B,则矩形OAPB的面积为 . 2热身练习、熟悉新知 2、 如图,点p是反比例函数 图像上一点,PD⊥X轴,PC⊥Y轴,则矩形PCOD的面积为 .xyOCDP8热身练习、熟悉新知3、如图,点P是反比例函数 图象上的一点,过P分别向x轴,y轴引垂线,垂足分别为A,C,阴影部分的面积为3,则这个反比例函数的解析式是 热身练习、熟悉新知4.如图,点A、B是双曲线 上的点,分别经过A、B两点向x轴、y轴作垂线,若S3=1,则S1+S2= 33S1S2S34分析:
由性质1得,
S1+S3=S2+S3=3
将S3=1代入得,
得,S1=S2=2
∴S1+S2=41、如图①,点P(2,1)是反比例函数 图象上的一点,PD⊥x轴于D,则△ POD的面积为1图①P(2,1)DoyxDo
S △ OPD= 热身训练、探索新知二1、如图①,点P(m,n)是反比例函数 图象上的任意一点,PD⊥x轴于D,则△ POD的面积为1图①P(m,n)oyxDo分析:
S △ OPD= 热身练习、熟悉新知则垂足为轴的垂线作过上任意一点是双曲线设,,)0(),(AxPkxynmP1=k导出新知请你思考面积性质21、如图,点P是反比例函数 图象上的任一点,过点P作PD⊥Y轴于D,则△POD的面积为 .D2热身练习、熟悉新知2、如图:点A在双曲线 上,AB⊥x轴于B,且△ AOB的面积S △ AOB=2,则k= -43、如图,在x轴上点P的右侧有一点D,过点D作x轴的垂线交双曲线 于点B,连结BO交AP于C,设△AOP的面积为S1,梯形BCPD面积为S2,则S1与S2的大小关系是S1 S2 。(选填“>”“<”或“=”)=4、如图,A、C是函数 的图象上的任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记Rt △ AOB的面积为S1,Rt △ OCD的面积为S2,则( )
A.S1>S2
B.S1< S2
C.S1=S2
D.S1和S2的大小关系不确定oA(m,n)CBDCA.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3 提高训练A1、如图,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为2,则这个反比
例函数的解析式为 . 点评:将△ABO通过“等积变换”同底等高变为△ABP拓展提升2、如图,过反比例函数 图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E, △ AOE与梯形ECDB的面积分别为 S1 、S2,比较它们的大小,可得 ( )
A.S1>S2 B.S1=S2
C.S1< S2 D.S1和S2的大小关系不确定ByxACBODE链接中考链接中考链接中考课堂小结通过这节课的学习,你有什么收获?⑴ 反比例函数图象上任意一点“对应的直角三角形”面积S1与k值有什么关系?
⑵ 反比例函数图象上任意一点“对应的矩形”面积S2与k值有什么关系?
必做题:课后小卷1--10
选做题:11、12
预习第27章第一节相似图形作业布置谢谢指导再见
