人教版数学八年级下册 第十七章 17.1.1 勾股定理 课件 共27张PPT
文档属性
| 名称 | 人教版数学八年级下册 第十七章 17.1.1 勾股定理 课件 共27张PPT |  | |
| 格式 | ppt | ||
| 文件大小 | 11.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-20 08:05:14 | ||
图片预览





文档简介
(共27张PPT)
黑白相间的地砖
故事引入,引发思考
相传两千多年前,古希腊著名的哲学家、数学家毕达哥拉斯去朋友家做客。在宴席上,其他的宾客都在尽情欢乐,只有毕达哥拉斯却看着朋友家的方砖地发起呆来。原来,朋友家的地是用一块块直角三角形形状的砖铺成的,黑白相间,非常美观大方。主人看到毕达哥拉斯的样子非常奇怪,就想过去问他,谁知,毕达哥拉斯突然恍然大悟的样子,站起来,大笑着跑回家去了。原来,他发现了地砖上的三个正方形存在某种数学关系。
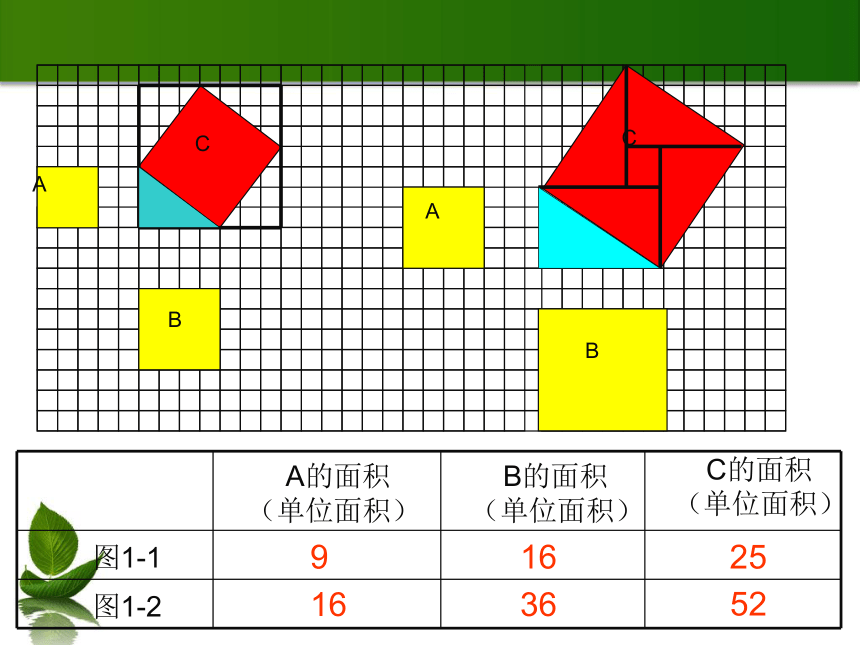
你知道他发现的三个正方形
黑白相间的地砖
之间存在着怎样的关系吗?
A
B
C
A
B
C
A的面积(单位面积)
B的面积(单位面积)
C的面积(单位面积)
图1-1
图1-2
9
16
25
16
36
52
A
B
C
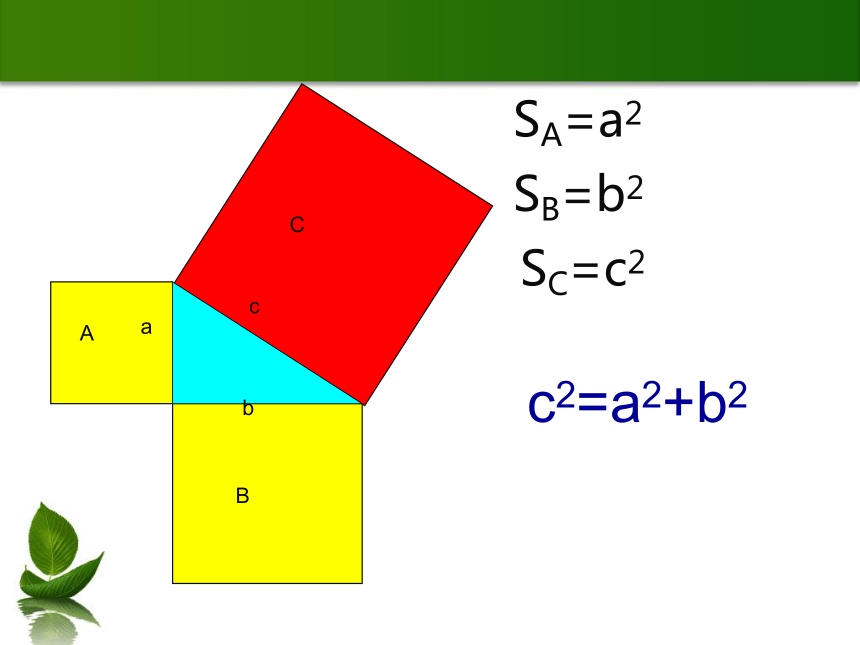
SA=a2
SB=b2
SC=c2
a
b
c
c2=a2+b2
动手做:画直角三角形ABC,使 ∠C=90°, AC=3cm BC=4cm.
动手量:它的斜边长是多少
动手算: 3、4、5各自的平方有什么关系
使用几何画板:对于任意直角三角形呢?两直角边的平方和都等于斜边的平方吗
(5cm)
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
a
b
c
A
B
C
D
c
b
a
a + b
2
2
c
2
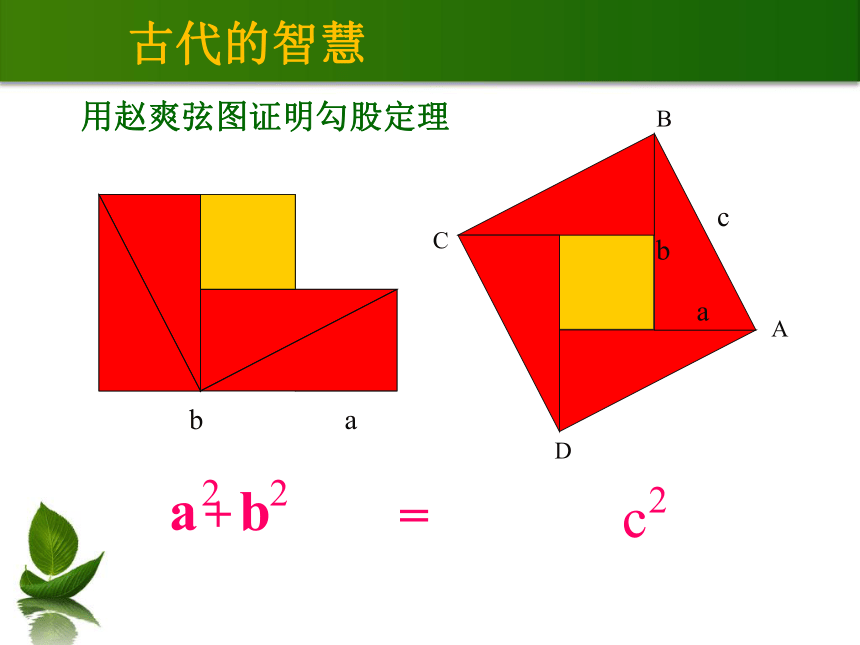
用赵爽弦图证明勾股定理
=
b
a
古代的智慧
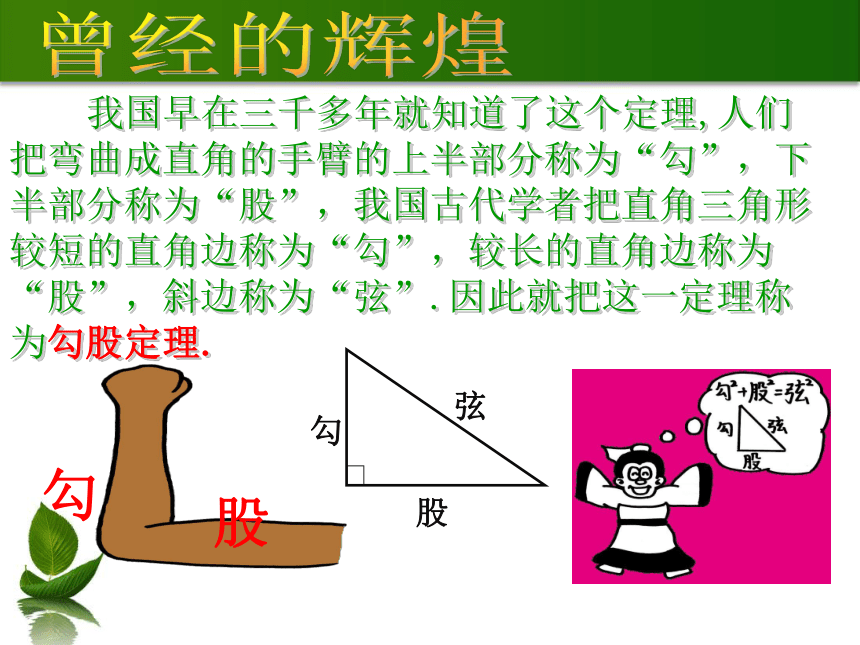
勾
股
勾
股
弦
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
a
b
c
c
a
b
1、拿出准备好的四个全等的直角三角形(设直角 三角形的两条直角边分别为a,b, 斜边为c);
2、你能用这四个直角三角形拼成一个正方形 吗?拼一拼试试看
3、你拼的正方形中是否含有以斜边c的正形?
4、你能否就你拼出的图说明a2+b2=c2?
c
a
b
c
a
b
c
a
b
c
a
b
∴a2+b2=c2
证明1:
∵ c2=
=b2-2ab+a2+ 2ab
=a2+b2
大正方的面积可以表示为
也可以表示为
c2
c
a
b
c
a
b
c
a
b
c
a
b
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
证明2:
∵
∴
8
6
算一算
AC2=AB2+BC2=62+82=100
∴AC=√100 = 10
A
B
C
求图中直角三角形的未知边的长度。
在Rt△ABC中,根据勾股定理,
15
17
BC2=AC2-AB2=172-152=64
∴BC=√64= 8
在Rt△ABC中,根据勾股定理,
A
B
C
例:如图,为得到池塘两岸A点和B点间的距离,
观测者在C点设桩,使△ABC为直角三角形,并测得
AC为100米,BC为80米.求A、B两点间的距离是多少?
A
B
C
解:如图,根据题意 得
Rt △ABC中,∠B=90°
AC=100米, BC=80米
由勾股定理得:AB2+BC2 =AC2
∴AB2 =AC2-BC2
=1002 - 802=602
∴AB=60(米)
答:A、B两点间的距离是60米.
1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.
=625
225
400
A
225
81
B
=144
想一想
A
B
C
D
7cm
2.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
勾股树
1、完成课本28页1、2、(必做)
2、一个长方形零件(如图),根据所给的尺寸(单位mm),求两孔中心A、B之间的距离.
A
B
90
160
40
40
1881年,伽菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”.
你能只用两个直角三角形说明 吗?
a
D
b
C
c
a
b
c
A
B
E
又
比较两式可知:a2+b2=c2
判 断 正 误
若直角三角形的两条边长为6cm、8cm,则第三边长一定为10cm.( )
×
6
8
6
8
(1)若a=5,b=12, 则c =___________.
试一试
在Rt△ABC中,
(2)若c=4,b= 2 ,则a = .
∠C=900 .
13
2
当c是斜边时, c2= a2+b2
当b是斜边时, b2= a2+c2
13或√119
如图,将长为10米的梯子AC斜靠 在墙上,BC长为6米。
(1)求梯子上端A到墙的底端B的距离AB。
(2)若梯子下部C向后移动2米到C1点,那么梯子上部A向下移动了多少米?
A
C
B
A1
C1
6
2
10
勾股
定理
重要的思想方法及数学思想
定理运用
定理内容
从特殊到一般、数形结合思想
黑白相间的地砖
故事引入,引发思考
相传两千多年前,古希腊著名的哲学家、数学家毕达哥拉斯去朋友家做客。在宴席上,其他的宾客都在尽情欢乐,只有毕达哥拉斯却看着朋友家的方砖地发起呆来。原来,朋友家的地是用一块块直角三角形形状的砖铺成的,黑白相间,非常美观大方。主人看到毕达哥拉斯的样子非常奇怪,就想过去问他,谁知,毕达哥拉斯突然恍然大悟的样子,站起来,大笑着跑回家去了。原来,他发现了地砖上的三个正方形存在某种数学关系。
你知道他发现的三个正方形
黑白相间的地砖
之间存在着怎样的关系吗?
A
B
C
A
B
C
A的面积(单位面积)
B的面积(单位面积)
C的面积(单位面积)
图1-1
图1-2
9
16
25
16
36
52
A
B
C
SA=a2
SB=b2
SC=c2
a
b
c
c2=a2+b2
动手做:画直角三角形ABC,使 ∠C=90°, AC=3cm BC=4cm.
动手量:它的斜边长是多少
动手算: 3、4、5各自的平方有什么关系
使用几何画板:对于任意直角三角形呢?两直角边的平方和都等于斜边的平方吗
(5cm)
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
a
b
c
A
B
C
D
c
b
a
a + b
2
2
c
2
用赵爽弦图证明勾股定理
=
b
a
古代的智慧
勾
股
勾
股
弦
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
a
b
c
c
a
b
1、拿出准备好的四个全等的直角三角形(设直角 三角形的两条直角边分别为a,b, 斜边为c);
2、你能用这四个直角三角形拼成一个正方形 吗?拼一拼试试看
3、你拼的正方形中是否含有以斜边c的正形?
4、你能否就你拼出的图说明a2+b2=c2?
c
a
b
c
a
b
c
a
b
c
a
b
∴a2+b2=c2
证明1:
∵ c2=
=b2-2ab+a2+ 2ab
=a2+b2
大正方的面积可以表示为
也可以表示为
c2
c
a
b
c
a
b
c
a
b
c
a
b
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
证明2:
∵
∴
8
6
算一算
AC2=AB2+BC2=62+82=100
∴AC=√100 = 10
A
B
C
求图中直角三角形的未知边的长度。
在Rt△ABC中,根据勾股定理,
15
17
BC2=AC2-AB2=172-152=64
∴BC=√64= 8
在Rt△ABC中,根据勾股定理,
A
B
C
例:如图,为得到池塘两岸A点和B点间的距离,
观测者在C点设桩,使△ABC为直角三角形,并测得
AC为100米,BC为80米.求A、B两点间的距离是多少?
A
B
C
解:如图,根据题意 得
Rt △ABC中,∠B=90°
AC=100米, BC=80米
由勾股定理得:AB2+BC2 =AC2
∴AB2 =AC2-BC2
=1002 - 802=602
∴AB=60(米)
答:A、B两点间的距离是60米.
1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.
=625
225
400
A
225
81
B
=144
想一想
A
B
C
D
7cm
2.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
勾股树
1、完成课本28页1、2、(必做)
2、一个长方形零件(如图),根据所给的尺寸(单位mm),求两孔中心A、B之间的距离.
A
B
90
160
40
40
1881年,伽菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”.
你能只用两个直角三角形说明 吗?
a
D
b
C
c
a
b
c
A
B
E
又
比较两式可知:a2+b2=c2
判 断 正 误
若直角三角形的两条边长为6cm、8cm,则第三边长一定为10cm.( )
×
6
8
6
8
(1)若a=5,b=12, 则c =___________.
试一试
在Rt△ABC中,
(2)若c=4,b= 2 ,则a = .
∠C=900 .
13
2
当c是斜边时, c2= a2+b2
当b是斜边时, b2= a2+c2
13或√119
如图,将长为10米的梯子AC斜靠 在墙上,BC长为6米。
(1)求梯子上端A到墙的底端B的距离AB。
(2)若梯子下部C向后移动2米到C1点,那么梯子上部A向下移动了多少米?
A
C
B
A1
C1
6
2
10
勾股
定理
重要的思想方法及数学思想
定理运用
定理内容
从特殊到一般、数形结合思想
