山东省东明县玉成中学2019年八年级数学17.2《勾股定理的逆定理》同步提高测试
文档属性
| 名称 | 山东省东明县玉成中学2019年八年级数学17.2《勾股定理的逆定理》同步提高测试 |

|
|
| 格式 | zip | ||
| 文件大小 | 156.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-20 00:00:00 | ||
图片预览


文档简介
八年级数学17.2《勾股定理的逆定理》同步提高测试
一、选择题:
1、若线段a,b,c组成Rt△,则它们的比可能为(???? )
A.2:3:4? B.3:4:6? C.5:12:13?? ? D.4:6:7
2、△ABC的三边分别是7、24、25,则三角形的最大内角的度数是( )
A.45°? B.60°? C.90°?? ? D.30°
3、如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,则AD的长为( )
A.13? B.16? C.15?? ? D.12
4、如图,由四个边长为1的小正方形构成一个大正方形,连接小正方形的三个顶点,可得到△ABC,则△ABC中BC边上的高是( )
A.3√2/2? B.3/2? C.2.5?? ? D.2
5、△ABC的三边为a、b、c,且(a+b)(a﹣b)=c2,则(???? )
A.△ABC是锐角三角形??? ? B.c边的对角是直角
C.△ABC是钝角三角形??? ? D.a边的对角是直角
6、满足下列条件的△ABC,不是直角三角形的是( )
A.b2=a2﹣c2 B.a:b:c=3:4:5
C.∠C=∠A﹣∠B?????? D.∠A:∠B:∠C=3:4:5
7、在△ABC,AB=AC=5,BC=6,若点P在边AC上移动,则BP的最小值是
A.4.8? B.6? C.4.5?? ? D.5
如图,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为( )
A.14? B.16? C.15?? ? D.17
9、(2018?东营)如图所示,圆柱的高AB=3,底面直径BC=3,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是( )
A. B. C. D.
10、△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )
A.1个 B.2个 C.3个 D.4个
如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,则∠ABC的度数为( )
A.45°? B.60°? C.75°?? ? D.30°
12、(2018?枣庄)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
A. B. C. D.
二、填空题:
13、已知△ABC的三边长分别为5,13,12,则△ABC的面积为 。
14、有长度为9cm、12cm、15cm、36cm、39cm的五根木棒,可搭成(首尾连接)直角三角形的个数为 个。
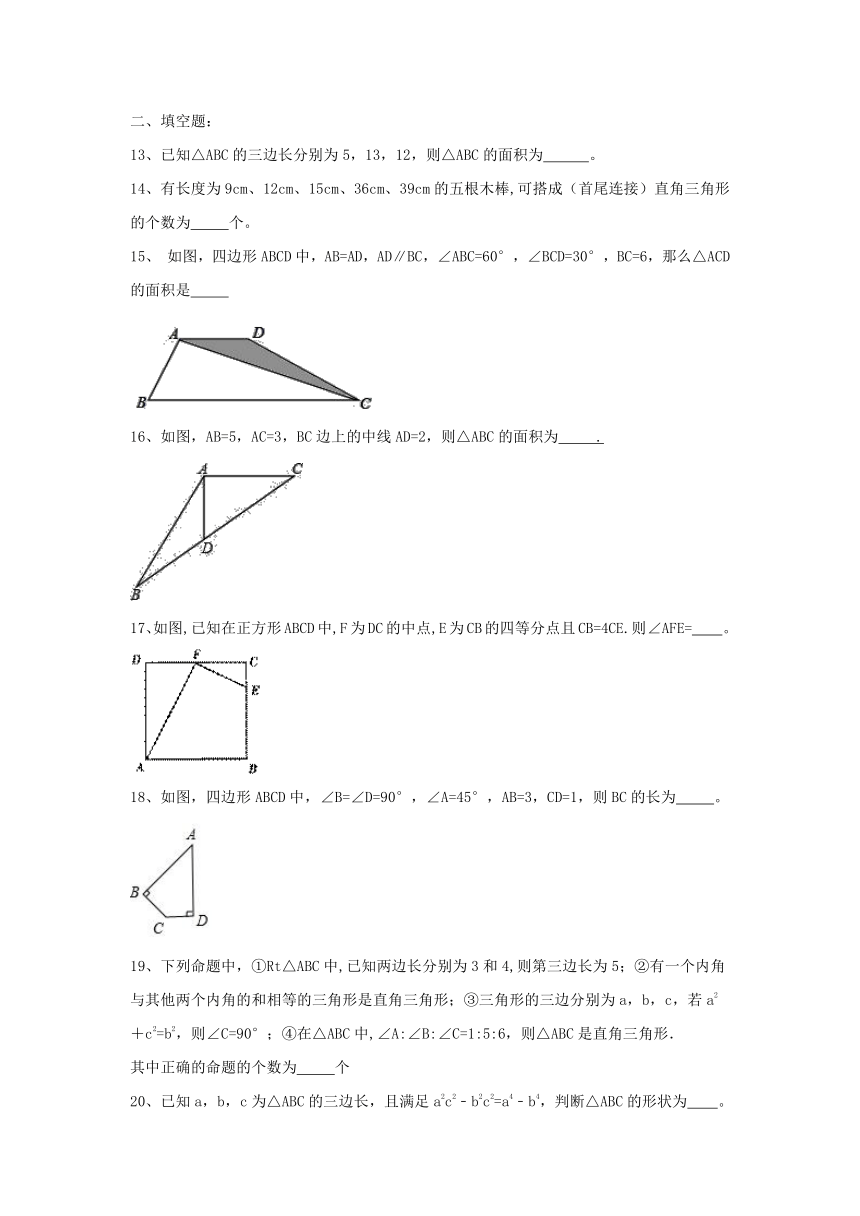
15、 如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是
16、如图,AB=5,AC=3,BC边上的中线AD=2,则△ABC的面积为 .
17、如图,已知在正方形ABCD中,F为DC的中点,E为CB的四等分点且CB=4CE.则∠AFE= 。
18、如图,四边形ABCD中,∠B=∠D=90°,∠A=45°,AB=3,CD=1,则BC的长为 。
19、下列命题中,①Rt△ABC中,已知两边长分别为3和4,则第三边长为5;②有一个内角与其他两个内角的和相等的三角形是直角三角形;③三角形的三边分别为a,b,c,若a2+c2=b2,则∠C=90°;④在△ABC中,∠A:∠B:∠C=1:5:6,则△ABC是直角三角形.
其中正确的命题的个数为 个
20、已知a,b,c为△ABC的三边长,且满足a2c2﹣b2c2=a4﹣b4,判断△ABC的形状为 。
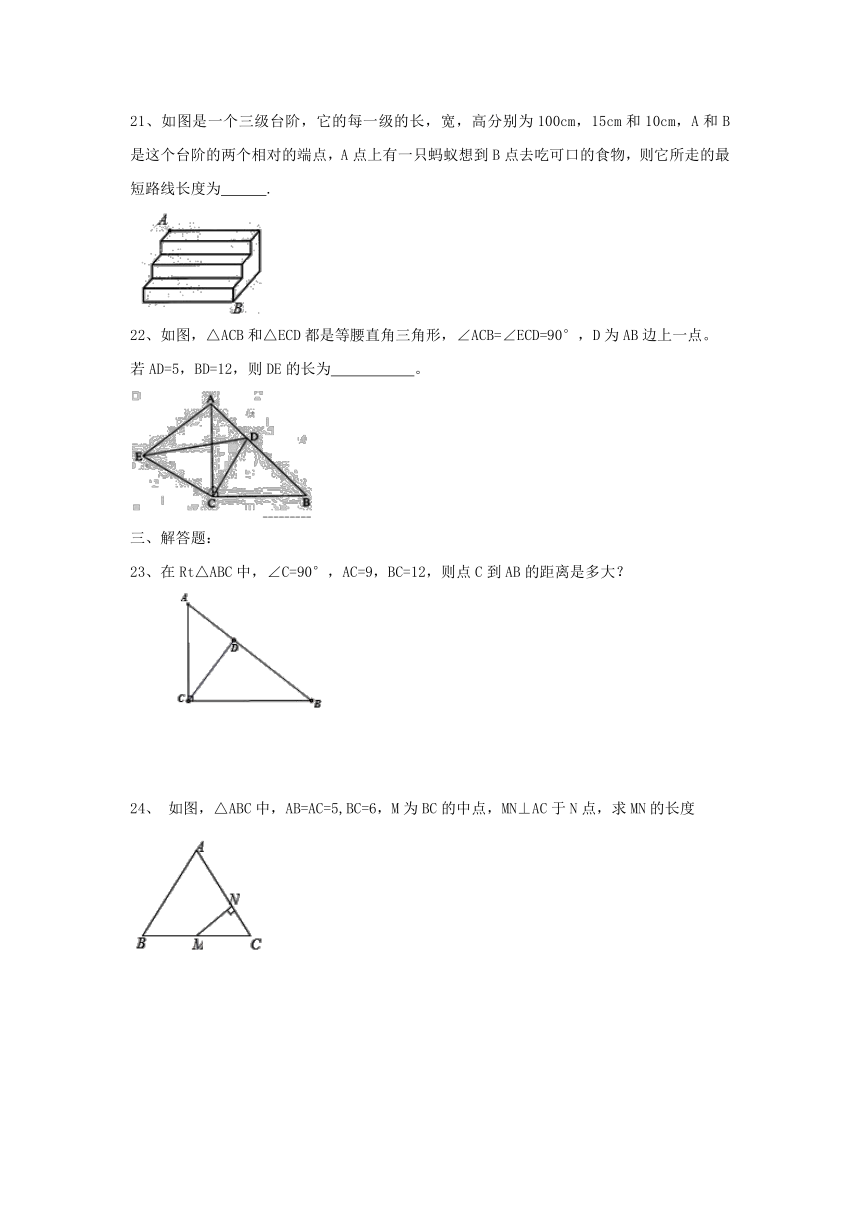
21、如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度为 .
22、如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点。
若AD=5,BD=12,则DE的长为 。?
三、解答题:
23、在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是多大?
24、 如图,△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC于N点,求MN的长度
25、如图所示是一块地的平面图,其中AD=4米,CD=3米,AB=13米,BC=12米,∠ADC=90°, 求这块地的面积。
26、在甲村至乙村的公路有一块山地正在开发,现有一C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险而需要暂时封锁?请通过计算进行说明.
27、已知a、b、c为△ABC的三边,且满足a2c2﹣b2c2=a4﹣b4,试判断△ABC的形状.
解:∵a2c2﹣b2c2=a4﹣b4,①
∴c2(a2﹣b2)=(a2+b2)(a2﹣b2).②
∴c2=a2+b2.③
∴△ABC是直角三角形.
问:
(1)在上述解题过程中,从哪一步开始出现错误?请写出该步的代号: ;
(2)错误的原因为 ;
(3)本题正确的解题过程:
参考答案
一、选择题:
1、C 2、C 3、A 4、A 5、D 6、D
7、A 8、A 9、C 10、C 11、A 12、A
二、填空题:
13、30
14、2
15、√3
16、6
17、90°
18、3-√2
19、2
20、等腰三角形或直角三角形
21、125
22、13
三、解答题:
24、连接AM,
∵AB=AC,点M为BC中点,
∴AM⊥CM,BM=CM,
∵AB=AC=5,BC=6,
∴BM=CM=3,
在Rt△ABM中,AB=5,BM=3,
∴根据勾股定理得:AM= ,
又S △AMC = MNAC/2= AMMC/2,
∴MN= .
25、24米2
26、公路AB需要暂时封锁.理由如下:如图,过C作CD⊥AB于D.
因为BC=400米,AC=300米,∠ACB=90°,所以根据勾股定理有AB=500米.
因为S△ABC=AB?CD/2=BC?AC/2所以CD=240米.
由于240米<250米,故有危险,因此AB段公路需要暂时封锁.
27、(1)③
(2)除式可能为零;
(3)∵a2c2﹣b2c2=a4﹣b4,
∴c2(a2﹣b2)=(a2+b2)(a2﹣b2),∴a2﹣b2=0或c2=a2+b2,
当a2﹣b2=0时,a=b;当c2=a2+b2时,∠C=90°,
∴△ABC是等腰三角形或直角三角形.
一、选择题:
1、若线段a,b,c组成Rt△,则它们的比可能为(???? )
A.2:3:4? B.3:4:6? C.5:12:13?? ? D.4:6:7
2、△ABC的三边分别是7、24、25,则三角形的最大内角的度数是( )
A.45°? B.60°? C.90°?? ? D.30°
3、如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,则AD的长为( )
A.13? B.16? C.15?? ? D.12
4、如图,由四个边长为1的小正方形构成一个大正方形,连接小正方形的三个顶点,可得到△ABC,则△ABC中BC边上的高是( )
A.3√2/2? B.3/2? C.2.5?? ? D.2
5、△ABC的三边为a、b、c,且(a+b)(a﹣b)=c2,则(???? )
A.△ABC是锐角三角形??? ? B.c边的对角是直角
C.△ABC是钝角三角形??? ? D.a边的对角是直角
6、满足下列条件的△ABC,不是直角三角形的是( )
A.b2=a2﹣c2 B.a:b:c=3:4:5
C.∠C=∠A﹣∠B?????? D.∠A:∠B:∠C=3:4:5
7、在△ABC,AB=AC=5,BC=6,若点P在边AC上移动,则BP的最小值是
A.4.8? B.6? C.4.5?? ? D.5
如图,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为( )
A.14? B.16? C.15?? ? D.17
9、(2018?东营)如图所示,圆柱的高AB=3,底面直径BC=3,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是( )
A. B. C. D.
10、△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )
A.1个 B.2个 C.3个 D.4个
如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,则∠ABC的度数为( )
A.45°? B.60°? C.75°?? ? D.30°
12、(2018?枣庄)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
A. B. C. D.
二、填空题:
13、已知△ABC的三边长分别为5,13,12,则△ABC的面积为 。
14、有长度为9cm、12cm、15cm、36cm、39cm的五根木棒,可搭成(首尾连接)直角三角形的个数为 个。
15、 如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是
16、如图,AB=5,AC=3,BC边上的中线AD=2,则△ABC的面积为 .
17、如图,已知在正方形ABCD中,F为DC的中点,E为CB的四等分点且CB=4CE.则∠AFE= 。
18、如图,四边形ABCD中,∠B=∠D=90°,∠A=45°,AB=3,CD=1,则BC的长为 。
19、下列命题中,①Rt△ABC中,已知两边长分别为3和4,则第三边长为5;②有一个内角与其他两个内角的和相等的三角形是直角三角形;③三角形的三边分别为a,b,c,若a2+c2=b2,则∠C=90°;④在△ABC中,∠A:∠B:∠C=1:5:6,则△ABC是直角三角形.
其中正确的命题的个数为 个
20、已知a,b,c为△ABC的三边长,且满足a2c2﹣b2c2=a4﹣b4,判断△ABC的形状为 。
21、如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度为 .
22、如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点。
若AD=5,BD=12,则DE的长为 。?
三、解答题:
23、在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是多大?
24、 如图,△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC于N点,求MN的长度
25、如图所示是一块地的平面图,其中AD=4米,CD=3米,AB=13米,BC=12米,∠ADC=90°, 求这块地的面积。
26、在甲村至乙村的公路有一块山地正在开发,现有一C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险而需要暂时封锁?请通过计算进行说明.
27、已知a、b、c为△ABC的三边,且满足a2c2﹣b2c2=a4﹣b4,试判断△ABC的形状.
解:∵a2c2﹣b2c2=a4﹣b4,①
∴c2(a2﹣b2)=(a2+b2)(a2﹣b2).②
∴c2=a2+b2.③
∴△ABC是直角三角形.
问:
(1)在上述解题过程中,从哪一步开始出现错误?请写出该步的代号: ;
(2)错误的原因为 ;
(3)本题正确的解题过程:
参考答案
一、选择题:
1、C 2、C 3、A 4、A 5、D 6、D
7、A 8、A 9、C 10、C 11、A 12、A
二、填空题:
13、30
14、2
15、√3
16、6
17、90°
18、3-√2
19、2
20、等腰三角形或直角三角形
21、125
22、13
三、解答题:
24、连接AM,
∵AB=AC,点M为BC中点,
∴AM⊥CM,BM=CM,
∵AB=AC=5,BC=6,
∴BM=CM=3,
在Rt△ABM中,AB=5,BM=3,
∴根据勾股定理得:AM= ,
又S △AMC = MNAC/2= AMMC/2,
∴MN= .
25、24米2
26、公路AB需要暂时封锁.理由如下:如图,过C作CD⊥AB于D.
因为BC=400米,AC=300米,∠ACB=90°,所以根据勾股定理有AB=500米.
因为S△ABC=AB?CD/2=BC?AC/2所以CD=240米.
由于240米<250米,故有危险,因此AB段公路需要暂时封锁.
27、(1)③
(2)除式可能为零;
(3)∵a2c2﹣b2c2=a4﹣b4,
∴c2(a2﹣b2)=(a2+b2)(a2﹣b2),∴a2﹣b2=0或c2=a2+b2,
当a2﹣b2=0时,a=b;当c2=a2+b2时,∠C=90°,
∴△ABC是等腰三角形或直角三角形.
