2019年春人教版数学八年级下册18.1.3平行四边形判定定理的简单应用
文档属性
| 名称 | 2019年春人教版数学八年级下册18.1.3平行四边形判定定理的简单应用 |  | |
| 格式 | zip | ||
| 文件大小 | 947.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-21 07:26:52 | ||
图片预览





文档简介
课件22张PPT。
平行四边形判定定理的简单应用1、通过探索平行四边形的判定,在探索中发展合情推理和逻辑推理的能力,进一步形成探索精神、动手能力、应用意识和抽象建模能力。
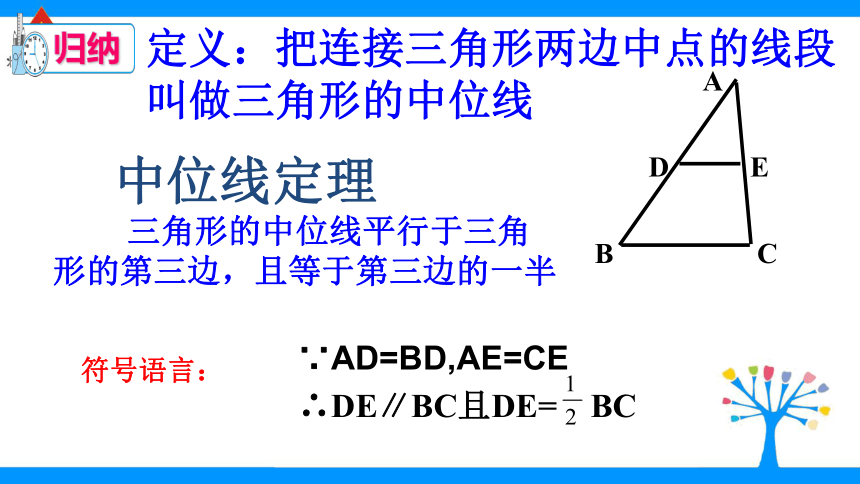
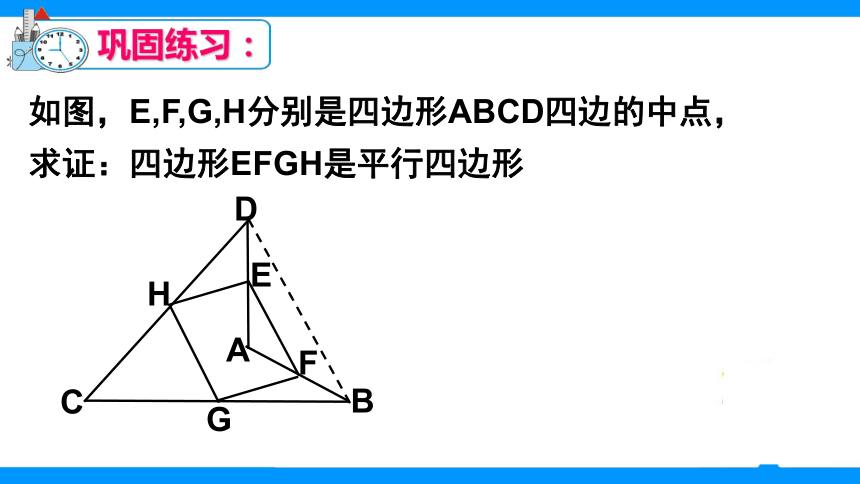
2、通过实例理解并掌握三角形的中位线定理。 到上一节课为止我们学习了几种判定平行四边形的方法?从角考虑从边考虑从对角线考虑例题:如图,点D、E分别是△ABC的边AB、AC的中点,求证DE∥BC且DE= BC证明:延长DE到F,使EF=DE,连接FC、DC、AF例题:如图,点D、E分别是△ABC的边AB、AC的中点,求证DE∥BC且DE= BCBCADE证明:延长DE到F,使EF=DE,连接FC、DC、AF∴四边形ADCF是平行四边形∴四边形DBCF是平行四边形∵AE=EC EF=DE定义:把连接三角形两边中点的线段叫做三角形的中位线 三角形的中位线平行于三角形的第三边,且等于第三边的一半中位线定理符号语言:∵AD=BD,AE=CE如图,E,F,G,H分别是四边形ABCD四边的中点,求证:四边形EFGH是平行四边形巩固练习:
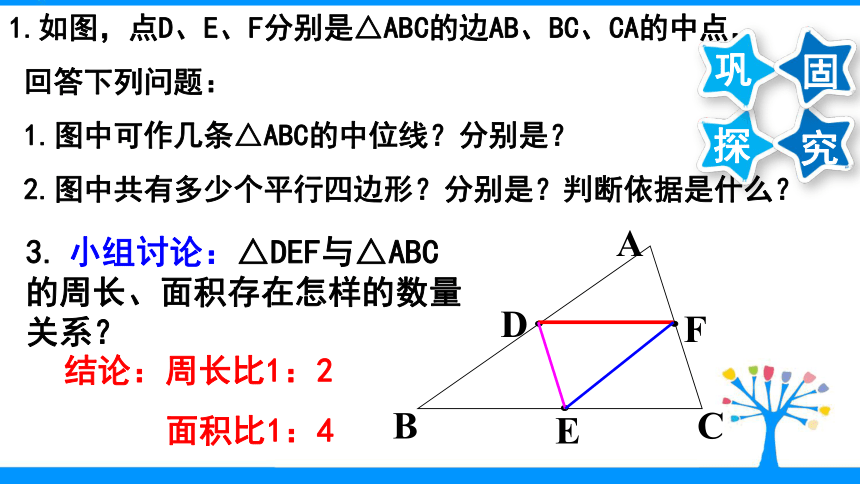
1.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,
回答下列问题:
1.图中可作几条△ABC的中位线?分别是?
2.图中共有多少个平行四边形?分别是?判断依据是什么?3. 小组讨论:△DEF与△ABC的周长、面积存在怎样的数量关系?结论:周长比1:2
面积比1:4
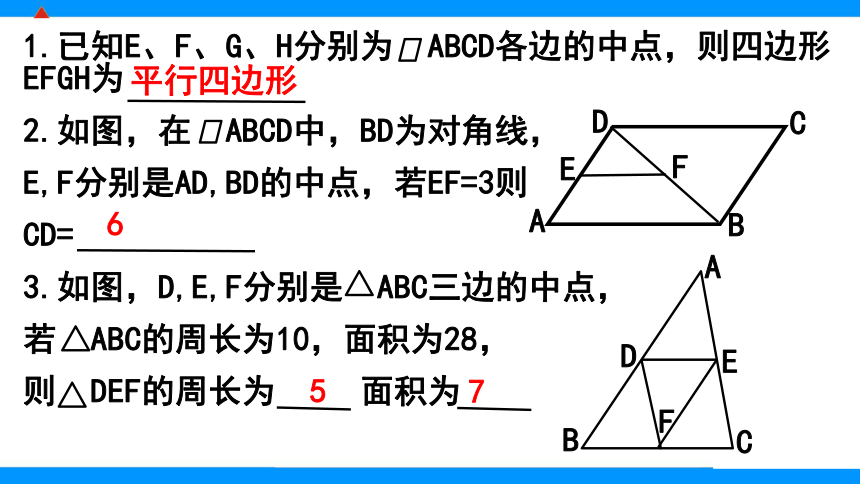
1.已知E、F、G、H分别为 ABCD各边的中点,则四边形EFGH为
2.如图,在 ABCD中,BD为对角线,
E,F分别是AD,BD的中点,若EF=3则
CD=
3.如图,D,E,F分别是 ABC三边的中点,
若 ABC的周长为10,面积为28,
则 DEF的周长为 面积为
平行四边形657
4.如图,在 ABCD中,对角线AC,BD交于点O,OE∥BC交CD于点E,若OE=3cm,则AD的长为
5.如图,在 ABCD中,对角线AC,BD
交于点O,E,FF分别,是AO,B分别是
AO,BO的中点,若AC+BD=24cm, OAB
的周长是18cm,则EF=
6.如图, ABC中,AB=4,AC=3,AD,AE
分别是其角平分线和中线,过C点作
CG⊥AD于点F,交AB于点G,连接EF,
则线段EF的长为
3cm6cm
7.如图,在 ABCD中,对角线AC,BD交于点O,E是边CD的中点,点F在BC的延长线上,且CF= BC
求证:四边形OCFE是平行四边形
7.如图,四边形ABCD中,∠A=90°,AB=4,AD=3,M是线段BC上的动点(但点M不与点B重合),N是AB上的定点,点E,F分别为DM,MN的中点,则EF的长度是否发生变化?说说你的理由
8变式:如图,四边形ABCD中,∠A=90°,AB=4,AD=3,点M、N是线段BC、AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF的长度是否发生变化?若不变化说说你的理由;若变化则最大值是多少?8变式:如图,四边形ABCD中,∠A=90°,AB=4,AD=3,点M、N是线段BC、AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF的长度是否发生变化?若不变化说说你的理由;若变化则最大值是多少?
ABCDN8变式:如图,四边形ABCD中,∠A=90°,AB=4,AD=3,点M、N是线段BC、AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF的长度是否发生变化?若不变化说说你的理由;若变化则最大值是多少?
ABCDN8变式:如图,四边形ABCD中,∠A=90°,AB=4,AD=3,点M、N是线段BC、AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF的长度是否发生变化?若不变化说说你的理由;若变化则最大值是多少?
ABCDN8变式:如图,四边形ABCD中,∠A=90°,AB=4,AD=3,点M、N是线段BC、AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF的长度是否发生变化?若不变化说说你的理由;若变化则最大值是多少?
ABCDN8变式:如图,四边形ABCD中,∠A=90°,AB=4,AD=3,点M、N是线段BC、AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF的长度是否发生变化?若不变化说说你的理由;若变化则最大值是多少?
ABCDN8变式:如图,四边形ABCD中,∠A=90°,AB=4,AD=3,点M、N是线段BC、AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF的长度是否发生变化?若不变化说说你的理由;若变化则最大值是多少?
ABCDN8变式:如图,四边形ABCD中,∠A=90°,AB=4,AD=3,点M、N是线段BC、AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF的长度是否发生变化?若不变化说说你的理由;若变化则最大值是多少?
ABCD(N)平行四边形判定定理的简单应用
1.把连接三角形两边中点的线段叫做三角形的中位线
2.三角形的中位线平行于三角形的第三边,且等于第三边的一半
3.周长比1:2
面积比1:4
再见
平行四边形判定定理的简单应用1、通过探索平行四边形的判定,在探索中发展合情推理和逻辑推理的能力,进一步形成探索精神、动手能力、应用意识和抽象建模能力。
2、通过实例理解并掌握三角形的中位线定理。 到上一节课为止我们学习了几种判定平行四边形的方法?从角考虑从边考虑从对角线考虑例题:如图,点D、E分别是△ABC的边AB、AC的中点,求证DE∥BC且DE= BC证明:延长DE到F,使EF=DE,连接FC、DC、AF例题:如图,点D、E分别是△ABC的边AB、AC的中点,求证DE∥BC且DE= BCBCADE证明:延长DE到F,使EF=DE,连接FC、DC、AF∴四边形ADCF是平行四边形∴四边形DBCF是平行四边形∵AE=EC EF=DE定义:把连接三角形两边中点的线段叫做三角形的中位线 三角形的中位线平行于三角形的第三边,且等于第三边的一半中位线定理符号语言:∵AD=BD,AE=CE如图,E,F,G,H分别是四边形ABCD四边的中点,求证:四边形EFGH是平行四边形巩固练习:
1.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,
回答下列问题:
1.图中可作几条△ABC的中位线?分别是?
2.图中共有多少个平行四边形?分别是?判断依据是什么?3. 小组讨论:△DEF与△ABC的周长、面积存在怎样的数量关系?结论:周长比1:2
面积比1:4
1.已知E、F、G、H分别为 ABCD各边的中点,则四边形EFGH为
2.如图,在 ABCD中,BD为对角线,
E,F分别是AD,BD的中点,若EF=3则
CD=
3.如图,D,E,F分别是 ABC三边的中点,
若 ABC的周长为10,面积为28,
则 DEF的周长为 面积为
平行四边形657
4.如图,在 ABCD中,对角线AC,BD交于点O,OE∥BC交CD于点E,若OE=3cm,则AD的长为
5.如图,在 ABCD中,对角线AC,BD
交于点O,E,FF分别,是AO,B分别是
AO,BO的中点,若AC+BD=24cm, OAB
的周长是18cm,则EF=
6.如图, ABC中,AB=4,AC=3,AD,AE
分别是其角平分线和中线,过C点作
CG⊥AD于点F,交AB于点G,连接EF,
则线段EF的长为
3cm6cm
7.如图,在 ABCD中,对角线AC,BD交于点O,E是边CD的中点,点F在BC的延长线上,且CF= BC
求证:四边形OCFE是平行四边形
7.如图,四边形ABCD中,∠A=90°,AB=4,AD=3,M是线段BC上的动点(但点M不与点B重合),N是AB上的定点,点E,F分别为DM,MN的中点,则EF的长度是否发生变化?说说你的理由
8变式:如图,四边形ABCD中,∠A=90°,AB=4,AD=3,点M、N是线段BC、AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF的长度是否发生变化?若不变化说说你的理由;若变化则最大值是多少?8变式:如图,四边形ABCD中,∠A=90°,AB=4,AD=3,点M、N是线段BC、AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF的长度是否发生变化?若不变化说说你的理由;若变化则最大值是多少?
ABCDN8变式:如图,四边形ABCD中,∠A=90°,AB=4,AD=3,点M、N是线段BC、AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF的长度是否发生变化?若不变化说说你的理由;若变化则最大值是多少?
ABCDN8变式:如图,四边形ABCD中,∠A=90°,AB=4,AD=3,点M、N是线段BC、AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF的长度是否发生变化?若不变化说说你的理由;若变化则最大值是多少?
ABCDN8变式:如图,四边形ABCD中,∠A=90°,AB=4,AD=3,点M、N是线段BC、AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF的长度是否发生变化?若不变化说说你的理由;若变化则最大值是多少?
ABCDN8变式:如图,四边形ABCD中,∠A=90°,AB=4,AD=3,点M、N是线段BC、AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF的长度是否发生变化?若不变化说说你的理由;若变化则最大值是多少?
ABCDN8变式:如图,四边形ABCD中,∠A=90°,AB=4,AD=3,点M、N是线段BC、AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF的长度是否发生变化?若不变化说说你的理由;若变化则最大值是多少?
ABCDN8变式:如图,四边形ABCD中,∠A=90°,AB=4,AD=3,点M、N是线段BC、AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF的长度是否发生变化?若不变化说说你的理由;若变化则最大值是多少?
ABCD(N)平行四边形判定定理的简单应用
1.把连接三角形两边中点的线段叫做三角形的中位线
2.三角形的中位线平行于三角形的第三边,且等于第三边的一半
3.周长比1:2
面积比1:4
再见
