18.1.2 平行四边形的判定(1)课件(23张)
文档属性
| 名称 | 18.1.2 平行四边形的判定(1)课件(23张) |
|
|
| 格式 | zip | ||
| 文件大小 | 680.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-20 00:00:00 | ||
图片预览






文档简介
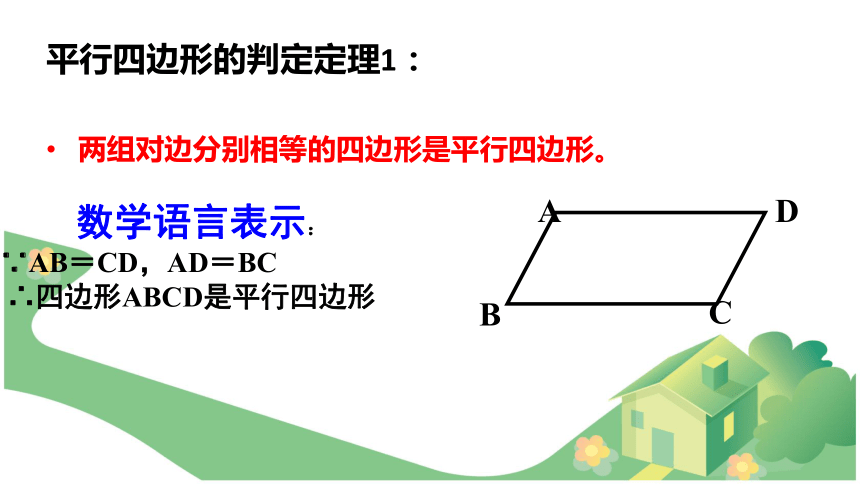
课件23张PPT。平行四边形的性质?对边平行且相等对角相等对角线互相平分∵ABCD是平行四边形
∴ OA=OC ,OB=OD∵ABCD是平行四边
形∴∠ABC=∠ADC
∠BAD=∠BCD∵ABCD是平行四边形
∴AB∥CD,AD∥BC
AB=CD,AD=BC 温故知新 根据平行四边形的性质思考:对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢? 18.1.2 平行四边形的判定(1)
如图将两长两短的四根细木条用小钉绞合在一起,做成一个四边形,使等长的木条成为对边.转动这个四边形,使它形状改变,在图形变化的过程中,它一直是一个平行四边形吗?已知:在四边形ABCD中, AB=CD,AD=BC
求证:四边形ABCD是平行四边形BDAC2134连结AC,在△ABC和△CDA中∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
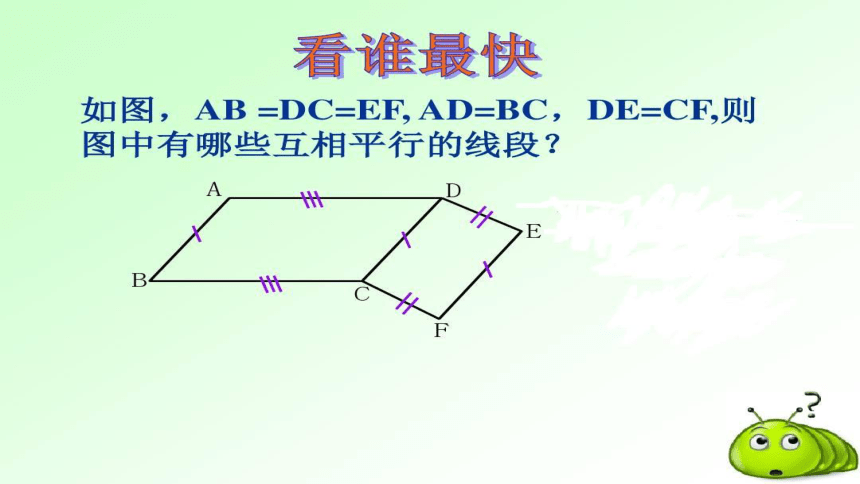
∴四边形ABCD是平行四边形。(平行四边形的定义)AB=CD AC=AC AD=BC∴△ABC≌△CDA(SSS)平行四边形的判定定理1: 两组对边分别相等的四边形是平行四边形。
数学语言表示:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
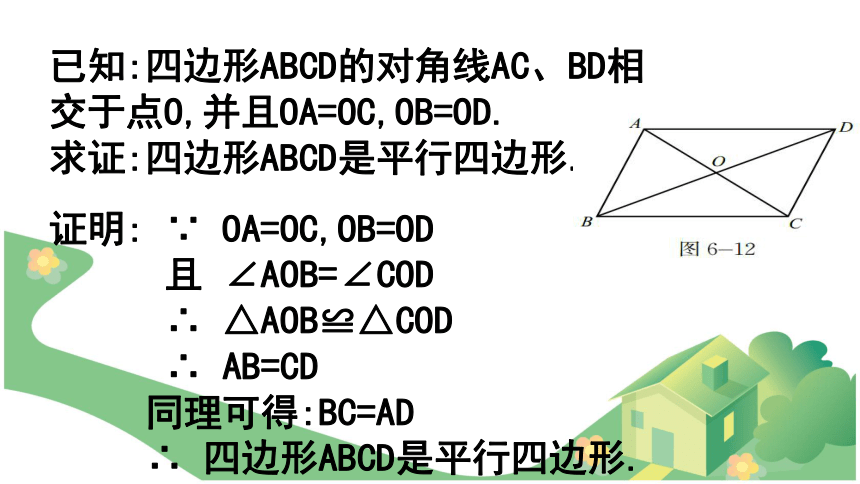
探究当一个四边形的对角线互相平分时,这个四边形是否为平行四边形呢?已知:四边形ABCD的对角线AC、BD相
交于点O,并且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明: ∵ OA=OC,OB=OD
且 ∠AOB=∠COD
∴ △AOB≌△COD
∴ AB=CD
同理可得:BC=AD
∴ 四边形ABCD是平行四边形.平行四边形的判定定理2:
对角线互相平分的四边形是平行四边形。
数学语言表示:
∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形
四边形 ABCD是平行四边形,点E,F是AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形。奇思妙想1.对于上述习题,若E,F继续移动到
线段AC延长线和反向延长线上,仍使AE=CF,则结论还成立吗?若成立,请证明. 变式题已知:四边形ABCD, ∠A=∠C,∠B=∠D
判断:四边形ABCD是否平行四边形
分析:∵∠A=∠C,∠B=∠D
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)
同理可证AB∥CD∴四边形ABCD是平行四边形探究 数学语言表示:
∵∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形平行四边形的判定定理3:
两组对角分别相等的四边形是平行四边形。1、下面分别给出了四边形ABCD,∠A, ∠B, ∠C, ∠D度数之比,其中能判断四边形ABCD是平行四边形的是( )
A、1:2:3:4 B、2:2:3:3 C、2:3:2:3 D、2:3:3:2学以致用D 。C 。。平行四边形的判定方法3两条对角线互相平分的四边形是平行四边形.4 两组对角分别相等
的四边形是平行四边形2两组对边分别相等
的四边形是平行四边形1 定义∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形 ∵AB=CD ,AD=BC
∴四边形ABCD是平行四边形∵∠A= ∠C,∠B= ∠D
∴四边形ABCD是平行四边形∵AO=CO ,BO=DO
∴四边形ABCD是平行四边形课堂检测1、在四边形ABCD中,AB=3 cm,BC=5 cm,那么当DC=______,AD=______时,四边形ABCD是平行四边形.2、如图,以△ABC的顶点A为圆心,以BC长为半径作弧,再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,连接AD,CD.若∠B=65°,则∠ADC的大小为______.3.如图,已知∠B=∠D,要使四边形ABCD成为平行四边形,需要添加一个条件是_______________.4.下列条件不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD∥BC B.∠A=∠C,∠B=∠D
C.AB=CD,AD=BC D.AB∥CD,AD=BC5.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图,将两根木条AC,BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形 6.一个四边形的四条边长依次是a,b,c,d,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形一定是____________,依据是__________________.7.如图,AB,CD相交于点O,AC∥DB,AO=BO,E,F分别是OC,OD的中点.求证:四边形AFBE是平行四边形.
本节课你学到什么?巩固了平行四边形的性质
学习了平行四边形的判定方法
培养了学生的逻辑推理能力
∴ OA=OC ,OB=OD∵ABCD是平行四边
形∴∠ABC=∠ADC
∠BAD=∠BCD∵ABCD是平行四边形
∴AB∥CD,AD∥BC
AB=CD,AD=BC 温故知新 根据平行四边形的性质思考:对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢? 18.1.2 平行四边形的判定(1)
如图将两长两短的四根细木条用小钉绞合在一起,做成一个四边形,使等长的木条成为对边.转动这个四边形,使它形状改变,在图形变化的过程中,它一直是一个平行四边形吗?已知:在四边形ABCD中, AB=CD,AD=BC
求证:四边形ABCD是平行四边形BDAC2134连结AC,在△ABC和△CDA中∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形。(平行四边形的定义)AB=CD AC=AC AD=BC∴△ABC≌△CDA(SSS)平行四边形的判定定理1: 两组对边分别相等的四边形是平行四边形。
数学语言表示:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
探究当一个四边形的对角线互相平分时,这个四边形是否为平行四边形呢?已知:四边形ABCD的对角线AC、BD相
交于点O,并且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明: ∵ OA=OC,OB=OD
且 ∠AOB=∠COD
∴ △AOB≌△COD
∴ AB=CD
同理可得:BC=AD
∴ 四边形ABCD是平行四边形.平行四边形的判定定理2:
对角线互相平分的四边形是平行四边形。
数学语言表示:
∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形
四边形 ABCD是平行四边形,点E,F是AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形。奇思妙想1.对于上述习题,若E,F继续移动到
线段AC延长线和反向延长线上,仍使AE=CF,则结论还成立吗?若成立,请证明. 变式题已知:四边形ABCD, ∠A=∠C,∠B=∠D
判断:四边形ABCD是否平行四边形
分析:∵∠A=∠C,∠B=∠D
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)
同理可证AB∥CD∴四边形ABCD是平行四边形探究 数学语言表示:
∵∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形平行四边形的判定定理3:
两组对角分别相等的四边形是平行四边形。1、下面分别给出了四边形ABCD,∠A, ∠B, ∠C, ∠D度数之比,其中能判断四边形ABCD是平行四边形的是( )
A、1:2:3:4 B、2:2:3:3 C、2:3:2:3 D、2:3:3:2学以致用D 。C 。。平行四边形的判定方法3两条对角线互相平分的四边形是平行四边形.4 两组对角分别相等
的四边形是平行四边形2两组对边分别相等
的四边形是平行四边形1 定义∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形 ∵AB=CD ,AD=BC
∴四边形ABCD是平行四边形∵∠A= ∠C,∠B= ∠D
∴四边形ABCD是平行四边形∵AO=CO ,BO=DO
∴四边形ABCD是平行四边形课堂检测1、在四边形ABCD中,AB=3 cm,BC=5 cm,那么当DC=______,AD=______时,四边形ABCD是平行四边形.2、如图,以△ABC的顶点A为圆心,以BC长为半径作弧,再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,连接AD,CD.若∠B=65°,则∠ADC的大小为______.3.如图,已知∠B=∠D,要使四边形ABCD成为平行四边形,需要添加一个条件是_______________.4.下列条件不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD∥BC B.∠A=∠C,∠B=∠D
C.AB=CD,AD=BC D.AB∥CD,AD=BC5.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图,将两根木条AC,BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形 6.一个四边形的四条边长依次是a,b,c,d,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形一定是____________,依据是__________________.7.如图,AB,CD相交于点O,AC∥DB,AO=BO,E,F分别是OC,OD的中点.求证:四边形AFBE是平行四边形.
本节课你学到什么?巩固了平行四边形的性质
学习了平行四边形的判定方法
培养了学生的逻辑推理能力
