4.1 认识三角形同步训练试题〖基础+综合+提高〗(含答案)
文档属性
| 名称 | 4.1 认识三角形同步训练试题〖基础+综合+提高〗(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 247.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-21 06:43:52 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
初中七年级数学下册第四章《认识三角形》同步训练〖基础+综合+提高〗
(总分:100分,用时:40分钟)
学校:___________姓名:___________班级:___________总分___________
一、单选题:(共10题,30分)
1.如果AD、AE、AF分别是ΔABC的中线、高和角平分线,且有一条在ΔABC的外部,则这个三角形是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.任意三角形
2.三角形三条中线的交点叫做三角形的( )
A.内心 B.外心 C.中心 D.重心
3.一个三角形的三条边长分别为1、2、x,则x的取值范围是( )
A.1≤x≤3 B.1<x≤3 C.1≤x<3 D.1<x<3
4.若一个三角形的两边长分别为3和7,则第三边长可能是( )
A.6 B.3 C.2 D.11
5.如图,在ΔABC中,D,E分别为BC,AD的中点,且 ,则为( )。
A.2 B.1
C. D.
6.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
B. C. D.
下列线段能构成三角形的是( )
A、2,2,4 B、3,4,5 C、1,2,3 D、2,3,6
8.如图,△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2=( )
?
A.360° B.250°
C.180° D.140°
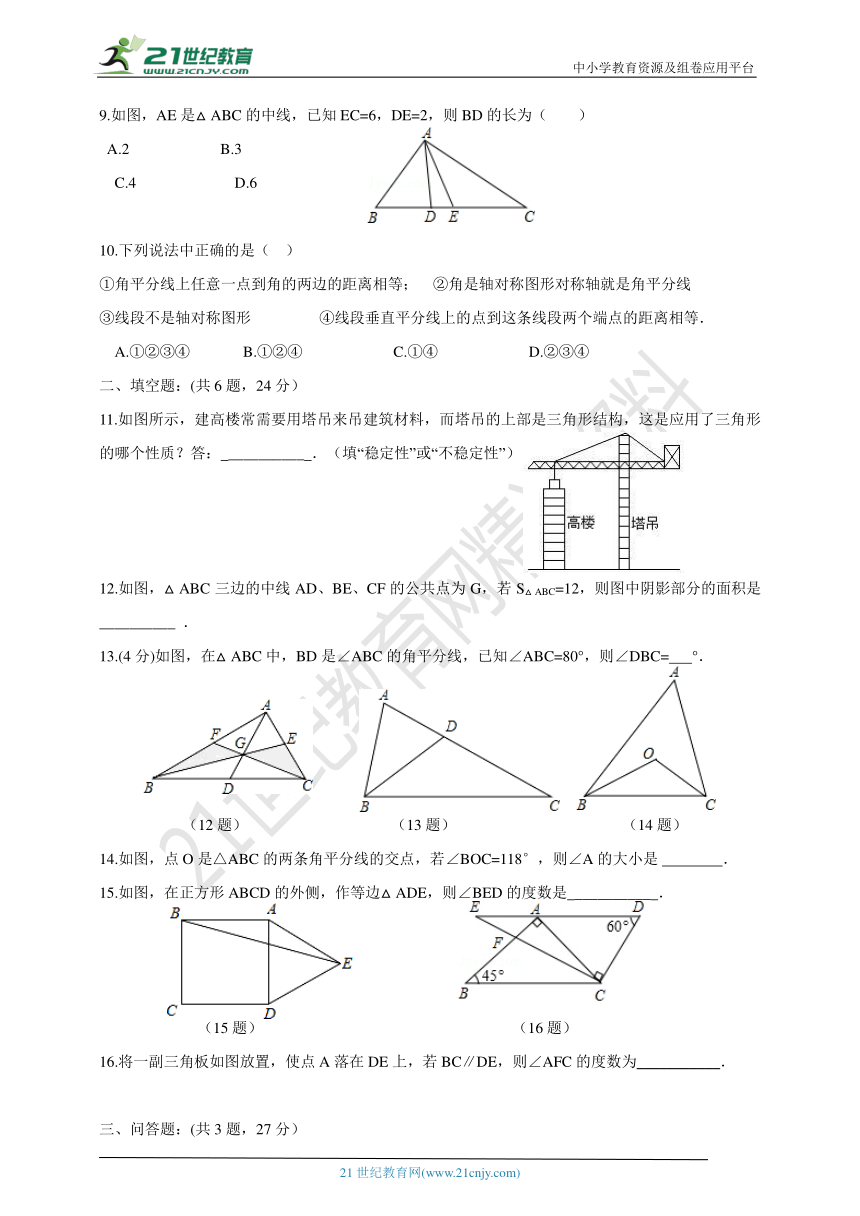
9.如图,AE是△ABC的中线,已知EC=6,DE=2,则BD的长为( )
A.2 B.3
C.4 D.6
10.下列说法中正确的是( )
①角平分线上任意一点到角的两边的距离相等; ②角是轴对称图形对称轴就是角平分线
③线段不是轴对称图形 ④线段垂直平分线上的点到这条线段两个端点的距离相等.
A.①②③④ B.①②④ C.①④ D.②③④
二、填空题:(共6题,24分)
11.如图所示,建高楼常需要用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是应用了三角形的哪个性质?答: __________ .(填“稳定性”或“不稳定性”)
12.如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是 __________ .
13.(4分)如图,在△ABC中,BD是∠ABC的角平分线,已知∠ABC=80°,则∠DBC= °.
?
(12题) (13题) (14题)
14.如图,点O是△ABC的两条角平分线的交点,若∠BOC=118°,则∠A的大小是? ????.
15.如图,在正方形ABCD的外侧,作等边△ADE,则∠BED的度数是 __________ .
(15题) (16题)
16.将一副三角板如图放置,使点A落在DE上,若BC∥DE,则∠AFC的度数为___________.
三、问答题:(共3题,27分)
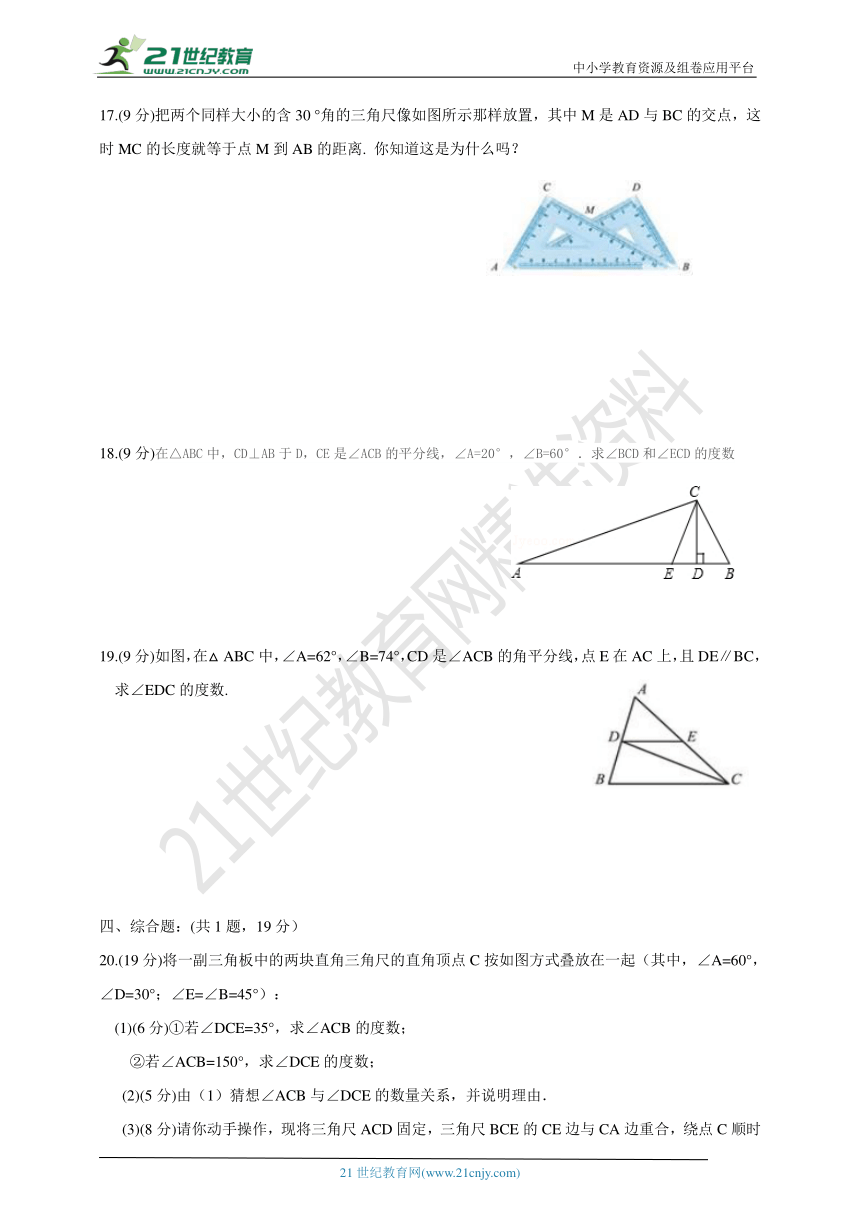
17.(9分)把两个同样大小的含30 °角的三角尺像如图所示那样放置,其中M是AD与BC的交点,这时MC的长度就等于点M到AB的距离. 你知道这是为什么吗?
18.(9分)在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数
19.(9分)如图,在△ABC中,∠A=62°,∠B=74°,CD是∠ACB的角平分线,点E在AC上,且DE∥BC,求∠EDC的度数.
四、综合题:(共1题,19分)
20.(19分)将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)(6分)①若∠DCE=35°,求∠ACB的度数;
②若∠ACB=150°,求∠DCE的度数;
(2)(5分)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)(8分)请你动手操作,现将三角尺ACD固定,三角尺BCE的CE边与CA边重合,绕点C顺时针方向旋转,当0°<∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.
参考答案与试题解析
选择题
1-5、CDDAB 6-10、ABBCC
二、填空题
11:稳定性 12.:4 13:40 14: 15:45° 16:75°
17.正确答案:解:过点M做MN⊥AB,
由题意可得:∠CAD=∠DAB=30°,
∵∠C=90°,MN⊥AB,
∴MC=MN(角平分线上的点到角的两边距离相等)
则MC的长度就等于点M到AB的距离.
18.正确答案:证明
19.正确答案:解:∵∠A=62°,∠B=74°
∴∠ACB=180°-62°-74°=44°
∵CD平分∠ACB
∴∠DCB=∠ACB=22°
∵DE∥BC
∴∠EDC=∠DCB=22°
20.
(1).正确答案:解:①∵∠ECB=90°,∠DCE=35°,
∴∠DCB=90°﹣35°=55°,
∴∠ACB=∠ACD+∠DCB=90°+55°=145°;
②∵∠ACB=150°,∠ACD=90°,
∴∠DCB=150°﹣90°=60°,
∴∠DCE=90°﹣60°=30°;
(2).正确答案:∠ACB+∠DCE=180°,
∵∠ACB=∠ACD+∠DCB=90°+∠DCB,
∴∠ACB+∠DCE=90°+∠DCB+∠DCE=90°+90°=180°;
(3).正确答案:存在,
当∠ACE=30°时,AD∥BC,
当∠ACE=∠E=45°时,AC∥BE,
当∠ACE=120°时,AD∥CE,
当∠ACE=135°时,BE∥CD,
当∠ACE=165°时,BE∥AD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
