2018--2019学年八年级物理下册 第十二章 杠杆 讲义 新版新人教版
文档属性
| 名称 | 2018--2019学年八年级物理下册 第十二章 杠杆 讲义 新版新人教版 | 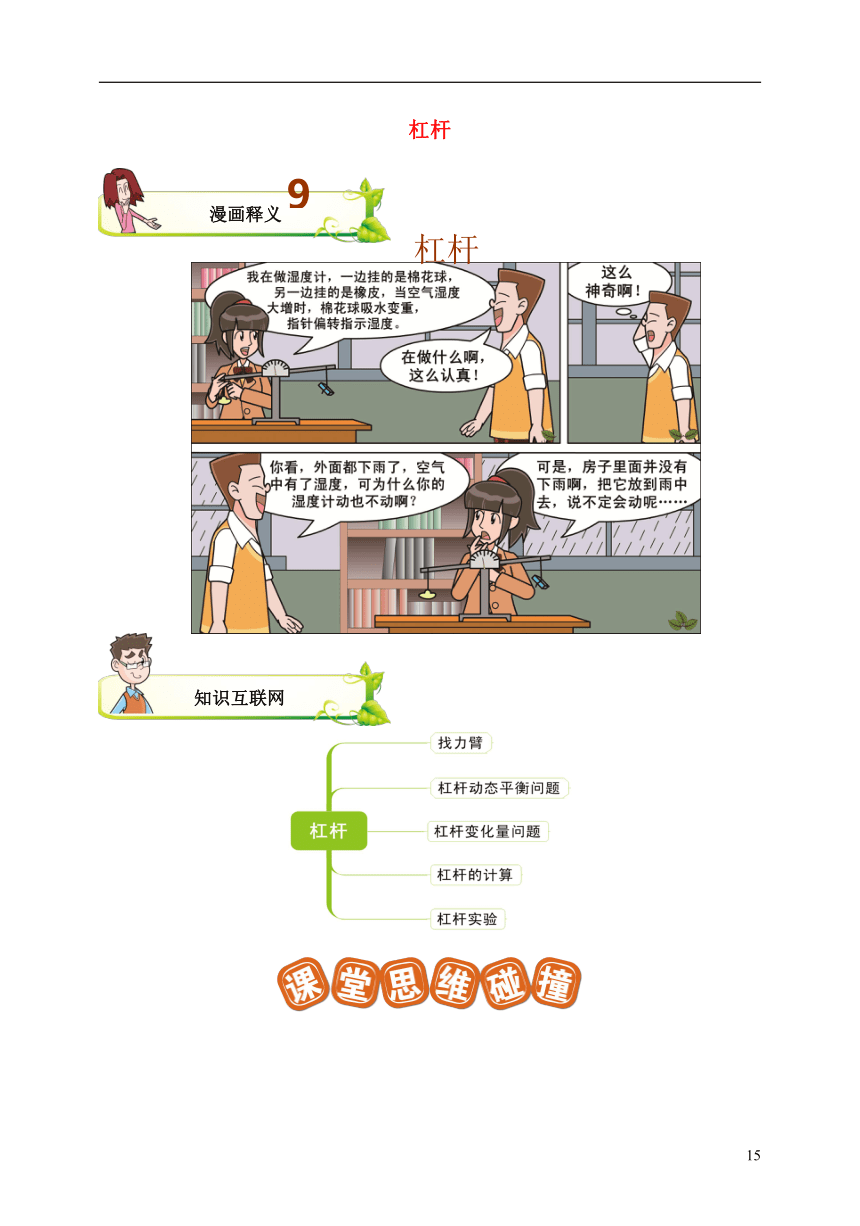 | |
| 格式 | zip | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-03-21 15:27:10 | ||
图片预览



文档简介
杠杆
如图所示, 重为G的物体放在水平面上, 用力F使其翻转, 请画出物体重力示意图和力F的力臂.
杠杆在我国古代就有了许多巧妙的应用, 护城河上安装使用的吊桥就是一个杠杆, 如图所示, 请画出动力F1与阻力F2的示意图, 并画出动力F1的力臂l1. (设吊桥质地均匀)
如图所示是利用杠杆原理制成的搬运煤气罐上楼的小车. 其中两处为轴连接. 以为支点请在图中画出的力臂(用表示).
如右图所示
如图所示, 地面上有一根两头粗细不同的木头, 现用竖直向上的力F将木头抬起, 在抬起的过程中, 力F的大小 ( )
A. 逐渐增大
B. 逐渐减小
C. 保持不变
D. 先增后减
C
一根直杆可绕轴O转动, 在直杆的中点挂一个重物, 在杆的另一端施加一个方向始终保持水平的力F, 如下图所示, 在力F使直杆从竖直位置慢慢抬起接近水平位置的过程中, 力F的大小变化情况应是 ( )
A. 一直在增大
B. 一直在减小
C. 先增大、后减小
D. 先减小、后增大
A
如图所示, 在轻质杆OB的中点A处, 悬挂有重为G的物体M, 在端点B施加方向始终跟杆垂直的拉力F, 杆从虚线位置沿逆时针方向匀速转至图示位置的过程中, 下列叙述中错误的是 ( )
A. 拉力F逐渐变大
B. 拉力F始终小于
C. 拉力F跟它力臂的乘积不变
D. 重物M对杠杆拉力的力臂逐渐变大
C
三个和尚挑水吃的故事相信大家耳熟能详, 图甲中和尚们商量出新的挑水方案: 胖和尚一人挑两小桶(如图乙) , 瘦和尚和小和尚两人合抬一大桶(如图丙) . 以下说法中不正确的是 ( )
A. 乙图中右水桶向下沉, 为保持水平平衡, 胖和尚可以将他的肩往右移动一点距离
B. 乙图中右水桶向下沉, 为保持水平平衡, 胖和尚可以将右水桶往左移动一点距离
C. 丙图中小和尚为减轻瘦和尚的负担, 可以让瘦和尚往前移动一点距离
D. 丙图中小和尚为减轻瘦和尚的负担, 可以将水桶往前移动一点距离
D
如图所示, 体积相同的铁块和铝块(ρ铁>ρ铝) , 挂在轻质杠杆AB的两端, 杠杆在水平位置平衡, 在下列情况下杠杆仍能在水平位置保持平衡的是 ( )
A. 将铁块和铝块同时去掉1N
B. 在杠杆两端各加挂一质量相等的钩码
C. 将铁块和铝块各切去一半
D. 将铁块和铝块同时向支点移动一段相同的距离
C
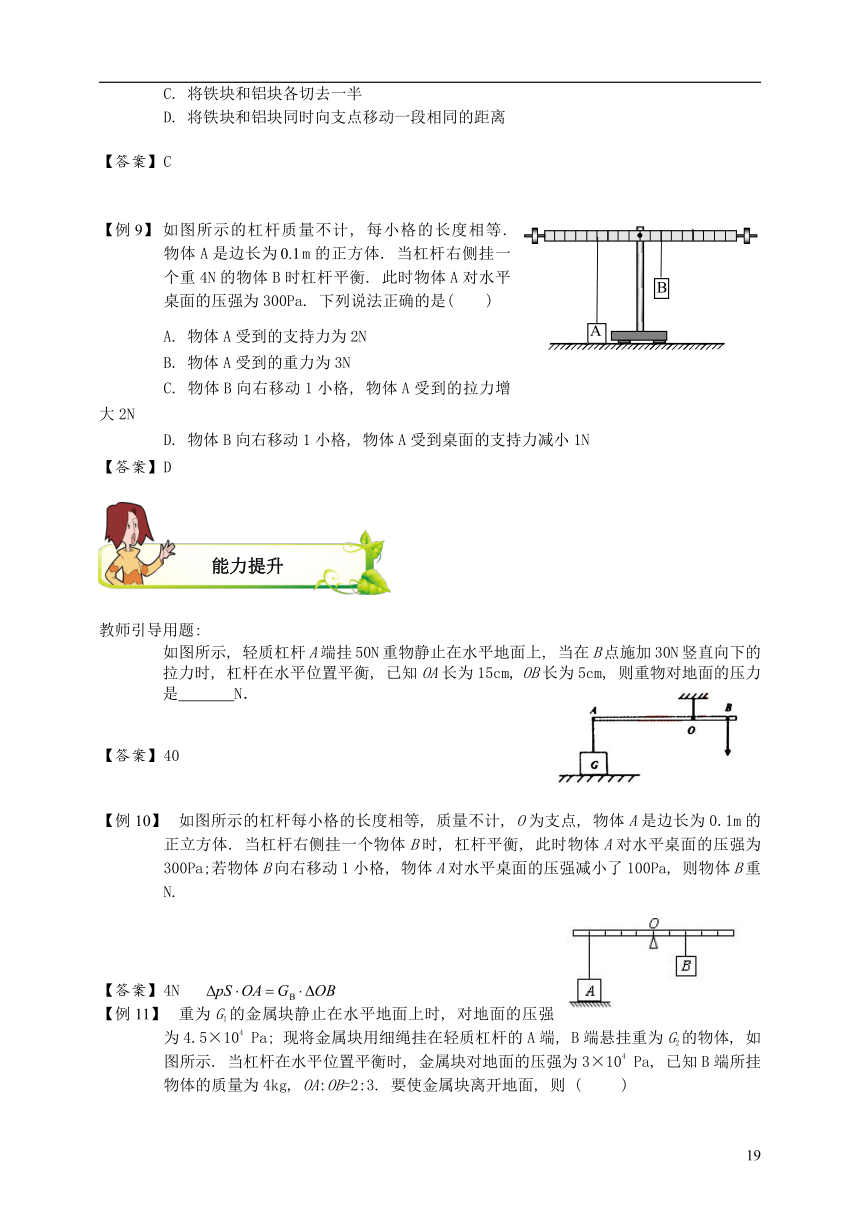
如图所示的杠杆质量不计, 每小格的长度相等. 物体A是边长为m的正方体. 当杠杆右侧挂一个重4N的物体B时杠杆平衡. 此时物体A对水平桌面的压强为300Pa. 下列说法正确的是( )
A. 物体A受到的支持力为2N
B. 物体A受到的重力为3N
C. 物体B向右移动1小格, 物体A受到的拉力增大2N
D. 物体B向右移动1小格, 物体A受到桌面的支持力减小1N
D
教师引导用题:
如图所示, 轻质杠杆A端挂50N重物静止在水平地面上, 当在B点施加30N竖直向下的拉力时, 杠杆在水平位置平衡, 已知OA长为15cm, OB长为5cm, 则重物对地面的压力是 N.
40
如图所示的杠杆每小格的长度相等, 质量不计, O为支点, 物体A是边长为0.1m的正立方体. 当杠杆右侧挂一个物体B时, 杠杆平衡, 此时物体A对水平桌面的压强为300Pa;若物体B向右移动1小格, 物体A对水平桌面的压强减小了100Pa, 则物体B重 N.
4N
重为G1的金属块静止在水平地面上时, 对地面的压强为4.5×104 Pa; 现将金属块用细绳挂在轻质杠杆的A端, B端悬挂重为G2的物体, 如图所示. 当杠杆在水平位置平衡时, 金属块对地面的压强为3×104 Pa, 已知B端所挂物体的质量为4kg, OA:OB=2:3. 要使金属块离开地面, 则 ( )
(g取10N/kg)
A. 轻质杠杆B端所挂物体的质量至少为5kg
B. 金属块对地面的压强只需减少1.5×104Pa
C. 只需移动支点的位置, 使支点左右两侧的力臂之比为2:9
D. 只需移动支点的位置, 使支点左右两侧的力臂之比为5:1
C
金属块甲静止在水平地面上, 对地面的压强是; 有一轻质杠杆AB, 支点为O, 且; 将甲挂在杠杆的B端, 在A端悬挂质量为4kg的物体乙时, 杠杆如图所示在水平位置平衡, 此时金属块甲对地面的压强变为. 当在杠杆A端改挂质量为 kg的物体时, 金属块甲对地面的压力刚好为零.
6
有一根杠杆, 长度为, 挂在其一端的物体重为, 挂在另一端的物体为, 问:
(1) 支点应在何处才能使杠杆平衡?
(2) 若杠杆两端所挂重物各增加, 支点应在何处才能使杠杆平衡?
(1) 设的物体挂在杠杆左端, 的物体挂在右端, 为支点, 如图甲
所示; 根据杠杆平衡条件
, , 则
解得 即支点距挂重为的物体一边处.
(2) 当两端所挂重物各增加时, 则
N, 为支点
如图乙所示, 根据杠杆平衡条件
,
则, 解得
支点距挂重为的物体一边处.
地面上有一根质量不均匀的大木棒, 长为1m, 小明从其左端用300N的力向上抬, 木棒刚好能离开地面; 之后小明又用200N的力从其右端向上抬, 木棒同样刚好能离开地面, 则木棒重力为 N, 重心离左端的距离为 m.
500; 0.4
如图所示, 质量分布均匀的长方形木板AB的长度L= 4m, 中央支于支架O上, A、B端分别用细绳AD、BC系于天花板上, 木板AB水平时, 绳AD、BC刚好绷直, 且AD绳竖直, BC绳与板AB成30°角, 已知细绳承受的最大拉力均为240N. 现有重为300N的小孩, 从O点出发, 沿OB 方向向B端缓慢行走, 那么绳将被拉紧; 在保证细绳不被拉断的情况下, 小孩向右行走的最大距离是 m; 若从O向A端行走, 则行走的最大距离是 m.
0.8m 1.6m
(1) S1 = 0.8m
(2)
如图所示, 质量为2kg的小铁块静止于水平导轨AB的A端(形状及尺寸在图中标出), 导轨AB及支架只可以绕着过D点的转动轴在图中竖直平面内转动. 现用一个沿导轨的拉力F通过细线拉铁块, 假定铁块起动后立即以0.1m/s的速度沿导轨匀速运动, 此时拉力F为10N. (导轨及支架ABCD的质量忽略不计, g=10N/kg). 则从铁块运动时起, 导轨及支架能保持静止的最长时间是 ( ??????? )
A. 7s B. 3s C. 11s D. 6s
B
小宁想探究杠杆平衡时动力和动力臂的关系. 实验过程中, 小宁保持阻力为3N, 阻力臂为0.2m不变, 然后改变动力臂L1和动力F1, 并保持杠杆水平平衡, 分别测量出动力臂L1和动力F1的数据如下表所示. 请你根据实验条件和实验数据帮助小宁归纳出动力F1跟动力臂L1的关系: 在 的条件下, F1 = .
L1/m
0.3
0.25
0.2
0.15
0.1
0.05
F1/N
2
2.4
3
4
6
12
杠杆平衡时, 当阻力与阻力臂的乘积保持不变时,
如图所示, 有一可绕中点O转动的轻质细杆, 杆上相邻刻度线之间的距离都是相等的. 小刚用这套实验器材探究杠杆平衡条件, 他使杆在水平位置平衡后, 在杆的A刻线处挂了2个钩码后, 在杆的B刻线处也挂了2个钩码, 杆在水平位置平衡. 当他在B刻线处改挂1个钩码后, 杆失去了平衡. 小刚由此得出结论: 只有施加在杆中点两侧的力大小相等时, 杆才能在水平位置平衡. 请你利用上述器材通过实验说明小刚的说法是错误的. 请你写出主要实验步骤和相应的实验现象.
主要实验步骤和现象:
(1) 使杆在水平位置平衡后, 在杆的中点O左侧距O点1格处挂2个钩码, 在杆的中点
O右侧距O点1格处挂2个钩码, 杆在水平位置平衡;
(2) 在杆的中点O左侧距O点1格处挂2个钩码, 在杆的中点O右侧距O点2格处挂1个钩码, 杆在水平位置平衡.
分析: 杆中点两侧施加的力大小不等, 杆在水平位置也平衡了, 说明小刚的说法是不正确的. (说明: 实验步骤中不写(1) 不扣分)
小芳用如图所示的装置研究杠杆的平衡条件. 小芳在杠杆左端第四格处挂了两个钩码, 左端第二个格处用弹簧测力计竖直向上拉使杠杆水平平衡. 测得此时弹簧测力计的示数为4N. 她反复做了几次实验, 分析得出杠杆的平衡条件为: 动力?支点到动力作用点的距离=阻力?支点到阻力作用点的距离. 请你只利用这套装置设计实验说明小芳的说法是不准确的. 请你写出实验步骤和实验现象.
实验步骤:
(1) 组装好器材, 调节杠杆两端螺母使杠杆在水平位置平衡后, 在杠杆左端第四格处挂了两个钩码, 左端第二个格处用弹簧测力计竖直向上拉使杠杆水平平衡, 记录弹簧测力计的示数为F1;
(2) 再保持弹簧测力计悬挂点不变, 将弹簧测力计斜向上拉, 杠杆水平平衡时, 记录弹簧测力计的示数为F2
实验现象: F1
实验台上有如下实验器材: 一个带支架的杠杆、一个量程为0~5N的弹簧测力计、七个质量均为100g的钩码和两段细绳. 请利用上述实验器材设计一个实验, 证明“在杠杆平衡时, 如果动力臂和阻力臂保持不变, 则动力的变化量跟阻力的变化量成正比”.
(1) 在如图所示的杠杆中, 点A表示钩码悬挂在杠杆上的位置, 请在合适的位置标出弹簧测力计施加拉力的作用点, 用B表示.
(2) 写出主要实验步骤, 画出记录实验数据的表格.
实验装置如图所示
实验步骤:
(1) 用细绳做一个绳套, 拴牢在杠杆的B位置处, 调节杠杆使其水平平衡, 把动力臂L动、阻力臂L阻记录在表格中. 将弹簧测力计的指针调节到零刻度线位置.
(2) 在A位置处挂1个钩码, 在B位置处竖直向上拉弹簧测力计, 使杠杆水平平衡, 将所挂钩码的质量m0、弹簧测力计示数F动0记录在表格中.
(3)在A点处加挂1个钩码, 在B点处竖直向上拉弹簧测力计, 使杠杆水平平衡, 将所挂钩码的总质量m1、弹簧测力计示数F动1记录在表格中.
(4) 仿照步骤③, 重复5次, 每次在A点处加挂1个钩码, 在B位置处竖直向上拉弹簧测力计, 使杠杆水平平衡; 将各次所挂钩码的总质量m2~m6、弹簧测力计示数
F动2~F动6记录在表格中.
(5) 根据F阻=G砝码=m砝码g, 分别算出每次施加在A位置的阻力大小F阻0~F阻6; 分别算出实验中动力变化量ΔF动1(F动1-F动0) ~ΔF动6(F动6-F动0) ; 分别算出与动力变化量对应的阻力变化量ΔF阻1(F阻1-F阻0) ~ΔF阻6(F阻6-F阻0) ; 将以上数据记录在表格中.
实验数据记录表格:
动力臂L动/cm
阻力臂L阻/cm
钩码质量m/g
动力F动/N
阻力F阻/N
动力变化量ΔF动/N
阻力变化量ΔF阻/N
(其他答案正确均可得分)
将重力为50N的物体甲放在水平地面上, 细绳的一端系于物体甲上表面的中央, 另一端竖直拉着杠杆的A端. 当把重力为20N的圆柱体乙悬挂在杠杆的B端时, 杠杆在水平位置平衡, 如图甲所示, 此时物体甲对水平地面的压强为p1. 当在物体乙下方加挂物体丙后, 如图乙所示, 物体甲对水平地面的压强为p2, 压力为6N. 且p1: p2=5:3, 物体丙的重力为 N.
2 (模块三 杠杆变化量问题)
如图甲所示是脚踏式翻盖垃圾桶的实物图, 翻盖的原理是由两个杠杆组合的示意图. 桶盖的质量为, 脚踏杆和其它连接杆的质量不计, 脚踏杆, , 桶盖和连接杆的尺寸如图乙所示. 把桶盖顶起, 脚对踏板压力至少为多大?
()
26.25N (模块四 杠杆的计算)
【解析】设脚对点的作用力为, 顶杆对点的作用力为, 顶杆对桶盖上点的作用力为, 根据杠杆平衡条件有: ①, ②,
桶盖受到的重力为:
①/②:
小李想测量食用油的密度ρ油, 他手边的测量工具只有刻度尺. 小李利用身边的器材设计出一个实验方案. 找来一根均匀轻质直硬棒, 用细线系在O点吊起, 硬棒在水平位置平衡, 将一密度未知的金属块B挂在硬棒左端C处, 另外找一个重物A挂在硬棒右端, 调节重物A的位置, 使硬棒在水平位置平衡, 此时重物挂在硬棒上的位置为D, 如图所示. 下面是小李测出ρ油 的部分实验步骤, 请你按照小李的实验思路, 将实验步骤补充完整:
(1) 用刻度尺测出OD的长度Lo;
(2) 将适量水倒入烧杯(水的密度为ρ水 为已知), 金属块B没入水中且不碰烧杯, 把重物A从D处移动到E处时(E点未标出), 硬棒再次在水平位置平衡,
, 将金属块B取出;
(3) 将适量油倒入另一烧杯, 金属块B没入油中且不碰烧杯, 将重物A从E处移动到F处时, 硬棒再次在水平位置平衡, , 将金属块B取出, 用抹布擦干;
(4) 利用上述测量出的物理量和题中的已知量计算的表达式为: .
(模块五 杠杆实验)
(2) 用刻度尺测出OE的长度l1
(3) 用刻度尺测出OF的长度l2
(4)
如图所示是环卫工人用的一种垃圾夹的结构示意图. 拉绳的一端固定在手把上, 另一端穿过空心管杆与两夹爪的一端相连. 当用力捏手把时, 夹爪在拉绳的作用下可夹持物体, 同时弹簧被压缩; 当松开手把时, 夹爪在弹簧的作用下恢复原状. 在使用过程中, 手把和夹爪分别是( )
A. 省力杠杆, 费力杠杆
B. 费力杠杆, 省力杠杆
C. 省力杠杆, 省力杠杆
D. 费力杠杆, 费力杠杆
A
如图所示, 一根质地均匀、粗细不同的胡萝卜平衡于支点O上, 若从O点处将萝卜锯断, 分给兔子和猴子, 则两段的重力大小为( )
A. 粗的一头重
B. 细的一头重
C. 两端一样重
D. 不能判断
A
如图所示, 直杆OA可绕O点转动, 直杆下端挂一重物G. 现用一个始终跟直杆垂直的力F将直杆由竖直位置缓慢转动到水平位置, 在转动过程中这个直杆( )
A. 始终是省力杠杆
B. 始终是费力杠杆
C. 先是费力杠杆, 后是省力杠杆
D. 先是省力杠杆, 后是费力杠杆
D
如图所示的杠杆处于平衡, 把A端所挂重物浸没在水中, 杠杆将失去平衡, 为使杠杆重新平衡应 ( )
A. 将支点O向A方向移动
B. 将支点O向B方向移动
C. 支点不动, B端再加挂砝码
D. 无法判断
B
小明单独站在地面上时, 对地面的压强为p1, 如图甲所示; 当他如图乙站立时, 他对地面的压强大小为p2; 当他如图丙站立时, 他对地面的压强大小为p3. 不计杠杆重力及轴摩擦. 已知小明重力为G, 杠杆AO:OB=1:2. 求物块G1、G2各为多少?
G=p1S人 ①
G1×2=(p1-p2)S人×1 ②
G2×2=(p3-p1)S人×1 ③
解得 G1=
解得 G2=
小阳想通过实验测出牛奶的密度ρ牛. 他找来一根直硬棒, 用细线系在硬棒的中点O并把硬棒悬挂起来, 硬棒在水平位置平衡. 如图所示, 他将石块M挂在硬棒的右端点E、密度为 ρ 的金属块N挂在硬棒的左端点C时, 硬棒在水平位置再次平衡, 如图所示. 当把金属块N浸没在待测密度的牛奶中, 把石块M从E点移动到D点时, 硬棒第三次在水平位置平衡. 如果用L1表示O、C两点间的距离, 用L2表示O、D两点间的距离, 则_______________.
