2018--2019学年八年级物理下册 第十章 浮力__船球模型 讲义 新版新人教版
文档属性
| 名称 | 2018--2019学年八年级物理下册 第十章 浮力__船球模型 讲义 新版新人教版 |
|
|
| 格式 | zip | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-03-21 00:00:00 | ||
图片预览


文档简介
船球模型
(多选) 一个漂浮在小型游泳池水面上的小船, 一个人从池水中捞出以下几种物体放入船中, 其中能使池中水面升高的是 ( )
A. 从池中捞铁块 B. 从水面上捞木块
C. 从池中捞石块 D. 将池中的一些水装入船中
AC
如图所示, 大杯中盛有液体, 装有密度均匀小球的小杯漂浮在液面上, 如果将小球取出并投入液体中, 液体的液面一定 ( )
A. 上升 B. 下降
C. 不变 D. 下降或不变
D
水槽中放一个小铁盒, 铁盒中放少许细线和一个铝块, 铁盒漂浮在水面. 现用细线把铝块拴在铁盒下面, 铁盒仍漂浮在水面, 如图所示; 讨论此时水槽中的水位以及铁盒浸入水中的体积, 说法正确的是 ( )
A. 水槽中水位不变, 铁盒浸入水中的体积变大
B. 水槽中水位下降, 铁盒浸入水中的体积不变
C. 水槽中水位上升, 铁盒浸入水中的体积不变
D. 水槽中水位不变, 铁盒浸入水中的体积变小
D
一、测密度模型
1、测质量模型(漂浮法)
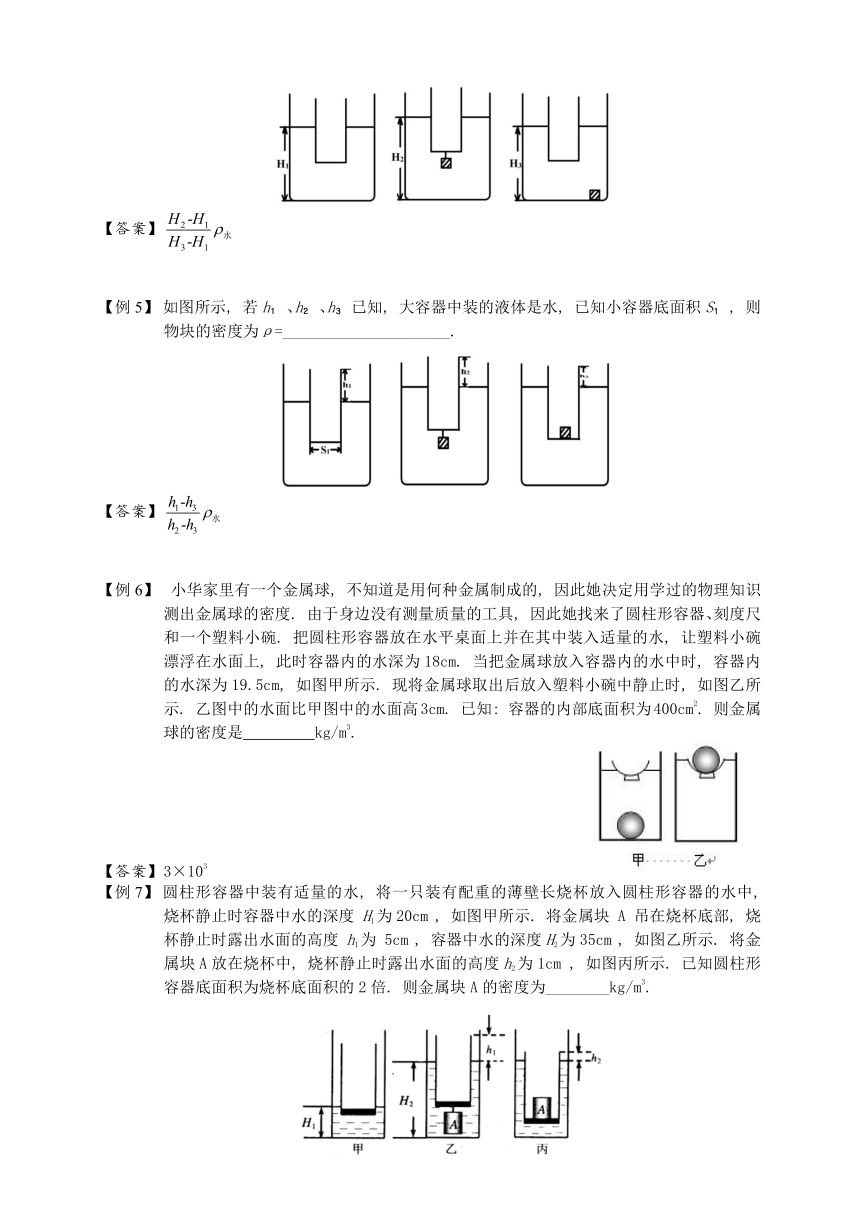
① mg=ρ液gS1(H2-H1) 条件: 外容器需直上直下
② mg=ρ液gS2(h2-h1) 条件: 内容器需直上直下
2、测体积模型
① 排水法: V球=(H4-H3) S1
② 悬挂法: V球=(h3-h4) S2
有一底面积为S的圆柱形容器中装有适量的水, 有一平底小试管漂浮在水中, 此时液面的高度为H?, 将一物块系在平底试管底部, 一起漂浮于水中, 此时液面高度为H?, 剪断细线, 物块沉底, 此时液面高度为H?, 则物块密度ρ=________________.
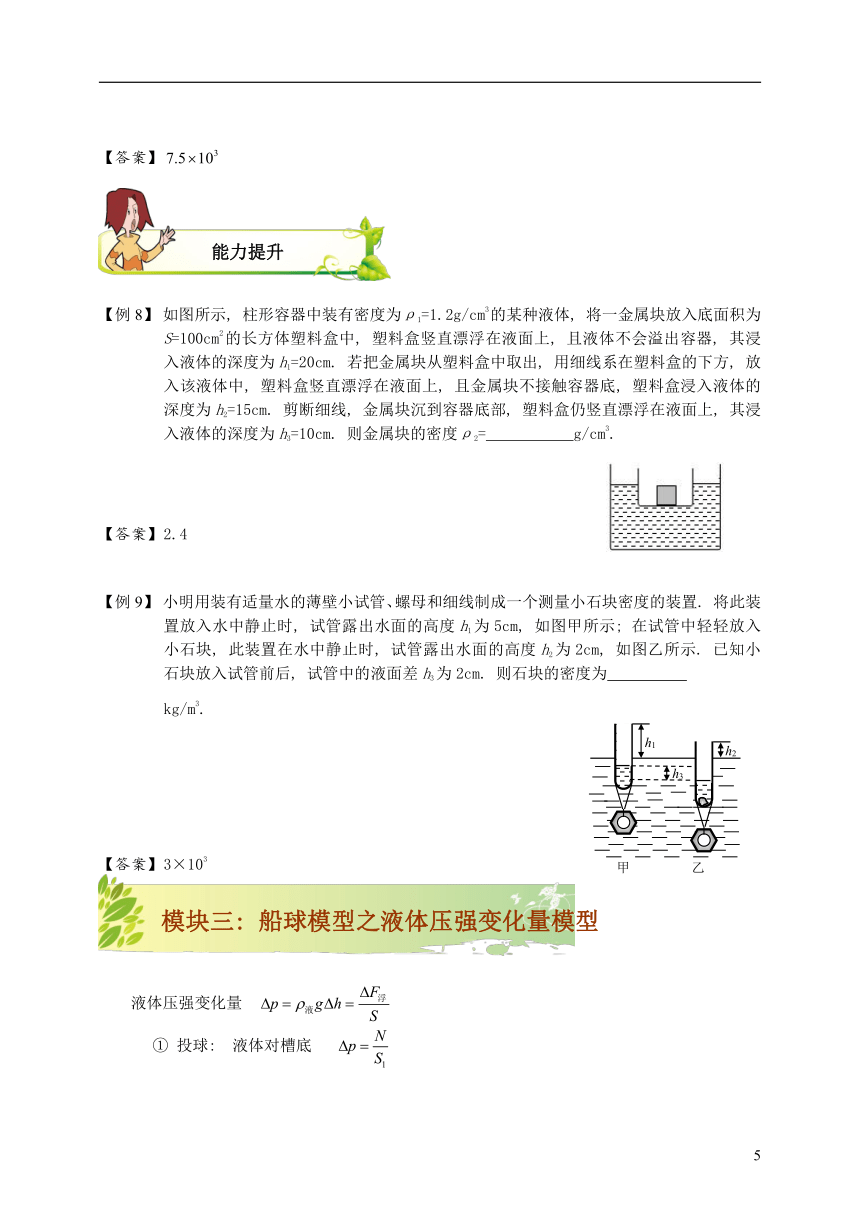
如图所示, 若h?、h?、h?已知, 大容器中装的液体是水, 已知小容器底面积S?, 则物块的密度为ρ=_____________________.
小华家里有一个金属球, 不知道是用何种金属制成的, 因此她决定用学过的物理知识测出金属球的密度. 由于身边没有测量质量的工具, 因此她找来了圆柱形容器、刻度尺和一个塑料小碗. 把圆柱形容器放在水平桌面上并在其中装入适量的水, 让塑料小碗漂浮在水面上, 此时容器内的水深为18cm. 当把金属球放入容器内的水中时, 容器内的水深为19.5cm, 如图甲所示. 现将金属球取出后放入塑料小碗中静止时, 如图乙所示. 乙图中的水面比甲图中的水面高3cm. 已知: 容器的内部底面积为400cm2. 则金属球的密度是 kg/m3.
3×103
圆柱形容器中装有适量的水, 将一只装有配重的薄壁长烧杯放入圆柱形容器的水中, 烧杯静止时容器中水的深度 H1为20cm , 如图甲所示. 将金属块 A 吊在烧杯底部, 烧杯静止时露出水面的高度 h1为 5cm , 容器中水的深度H2为35cm , 如图乙所示. 将金属块A放在烧杯中, 烧杯静止时露出水面的高度h2为1cm , 如图丙所示. 已知圆柱形容器底面积为烧杯底面积的2倍. 则金属块A的密度为________kg/m3.
如图所示, 柱形容器中装有密度为ρ1=1.2g/cm3的某种液体, 将一金属块放入底面积为S=100cm2的长方体塑料盒中, 塑料盒竖直漂浮在液面上, 且液体不会溢出容器, 其浸入液体的深度为h1=20cm. 若把金属块从塑料盒中取出, 用细线系在塑料盒的下方, 放入该液体中, 塑料盒竖直漂浮在液面上, 且金属块不接触容器底, 塑料盒浸入液体的深度为h2=15cm. 剪断细线, 金属块沉到容器底部, 塑料盒仍竖直漂浮在液面上, 其浸入液体的深度为h3=10cm. 则金属块的密度ρ2= g/cm3.
2.4
小明用装有适量水的薄壁小试管、螺母和细线制成一个测量小石块密度的装置. 将此装置放入水中静止时, 试管露出水面的高度h1为5cm, 如图甲所示; 在试管中轻轻放入小石块, 此装置在水中静止时, 试管露出水面的高度h2为2cm, 如图乙所示. 已知小石块放入试管前后, 试管中的液面差h3为2cm. 则石块的密度为
kg/m3.
3×103
液体压强变化量
① 投球: 液体对槽底
② 剪绳: 液体对槽底
如图所示, 在底面积为S的圆柱形水池底部有一个金属球(球与池底没有密合) , 圆柱型的水槽漂浮在池内的水面上, 此时水槽受到的浮力为F1. 若把金属球从水中捞出并放在水槽中漂浮在水池中, 此时水槽受到的浮力为F2, 捞起金属球前、后水池底受到水的压强变化量为p, 水的密度为ρ水. 根据上述条件可以求出 ( )
A. 金属球受的重力为F2 –F1–pS
B. 金属球被捞起前受的浮力为F2 –F1
C. 金属球被捞起前、后水槽底受水的压力减小了pS
D. 金属球被捞起前、后水槽排开水的体积增大了
D
如图所示, 将一个木块投入装有液体的水槽中, 处于漂浮状态, 现用大小为4N的力竖直向下压, 此时液体对水槽底部压强增大了. 又找来一个金属块用细线挂在木块的下面, 这时液面深度为; 剪断细线, 金属块下沉, 稳定后液面深度降低为, 金属块对水槽底部压力大小为3.2N, 求: 剪断后, 液体对水槽底部压强减少了多少? 液体密度为多少? ()
;
一冰块内冰封一合金物体, 将其放入盛有适量水, 底面积为的烧杯内, 正好悬浮在水中, 此时烧杯内的水对烧杯底的压强增加了; 当冰完全熔化后, 水对烧杯底的压强又变化了. 忽略烧杯内水的体积所受温度的影响, 当冰完全熔化后, 烧杯底对合金物体的支持力是 N. (冰的密度为, 取) .
0.44
如图所示, 底面积为200cm2的容器底部有一固定轻质弹簧, 弹簧上方连有一边长为10cm的正方体木块A, 当容器中水深为20cm时, 木块A有的体积浸在水中, 此时弹簧恰好处于自然状态, 没有发生形变. 向容器内缓慢加水, 当弹簧伸长了1cm时停止加水, 此时弹簧对木块拉力为1N. 加水前后容器底部受到水的压强变化了 Pa. (不计弹簧受到的浮力, g取10N/kg)
200
如图所示, 将挂在弹簧测力计下端高为8cm、横截面积为100cm2的柱形物块缓慢放入底面积为500cm2的圆柱形容器内的水中. 当物块直立静止时, 物块浸入水中深度为2cm, 弹簧测力计的示数为8N, 水对容器底部的压强为1.2×103Pa. 现向容器中加水, 当弹簧测力计的示数为5N时, 注入水的质量为m, 水对容器底部的压强为p, 柱形物块受到的浮力为F. 已知弹簧测力计的称量范围为0~10N, 刻度盘上0~10N刻度线之间的长度为10cm. 若g取10N/kg, 则下列说法中正确的是( )
A. 柱形物块所受重力大小为8N
B. 柱形物块受到的浮力F大小为3N
C. 水对容器底部的压强p为1.8×103Pa
D. 向容器中注入水的质量m为3.0kg
C
实验桌上有如图所示的下列器材, 请你利用这些器材, 测出小金属块的密度. 写出实验步骤(用字母表示测出的物理量, 水的密度用ρ水表示)及金属块的密度表达式.
实验步骤:
(1) 让小容器漂浮在水槽中的水面上, 量出这时水面到槽边沿的距离h1.
(2) 量出 , 量出这时水面到槽上边沿的距离h2.
(3) 将金属块从小容器中取出用细线系住没入槽内水中, 量出这时水面到槽上边沿的距
离h3. 金属块密度的表达式 金属 =
(2) 将小金属块放入漂浮在水面上的小容器内
(3)
爱好科技的小刚自己制作了一条小木船, 船上带有金属船锚, 船舷上表明了三种情况的排水量.
(1) 将锚放在船舱里, 当船静止在水槽中时观察对应的排水量为;
(2) 用细线拴住船锚, 悬挂在船下方的水中且完全浸没, 观察对应的排水量为, 此时水槽中的水面将 ; (选填“升高”、“降低”或“不变”) .
(3) 把细线放得更长些, 直至线松了, 锚沉在盆底, 记下此时对应的排水量为于是利用这些排水量测出了船锚的密度. 则锚的密度 .
不变; ρ水
实验桌上有如下器材: 细长平底试管一支(已知底面积为S)、小汤匙一个、抹布一块、刻度尺一把、大水槽一个(水槽的深度大于平底试管的高度)、足量的水、足量的细沙子、天平及配套砝码. 要求从实验桌上选择适当的器材, 设计一个实验证明: 在同种液体中, 固体所受的浮力大小跟排开液体的体积成正比. 要求: 写出主要的实验步骤并设计记录实验数据的表格.
(1) 把天平放在水平桌面上, 调节天平平衡; (有此项给1分, 没有扣1分).
(2) 用刻度尺测出试管的长度L并记录;
(3) 用药匙取适量的细沙装入试管, 用天平测出细沙和试管的总质量m1; 再将试管放入盛有水的水槽中, 使试管竖直漂浮在水面上静止, 用刻度尺测出试管露出水面的高度h1; 将m1、h1记录在表格内.
(4) 用抹布擦干试管, 用药匙再取适量的细沙装入试管, 用天平测出细沙和试管的总质量m2; 再将试管放入盛有水的水槽中, 使试管竖直漂浮在水面上静止, 用刻度尺测出试管露出水面的高度h2; 将m2、h2记录在表格内.
(5) 仿照步骤(4)再做4次实验, 测出细沙和试管的总质量m3、m4、m5、m6; 测出每次试管露出水面的高度h3、h4、h5、h6, 并将数值记录在表格内.
(6) 计算出每次试管浸入水中的深度(L-h)和排开水的体积V排=(L-h)S; 将数据记录在表管内.
(7) 根据物体漂浮时F浮=G物=mg, 可知试管每次漂浮时所受的浮力F浮.
(8) 分析F浮和试管排开水的体积V排确定两者的关系.
S=
实验次数
试管的长度L/cm
细沙和试管的总质量m/kg
重力G/N
试管露出水面高度h/cm
试管浸入水中深度(L-h)/cm
试管排开水的体积V排/cm3
浮力F浮/N
如图所示, 在盛有某种液体的圆柱形容器内放有一木块A, 在木块的下方用轻质细线悬挂一体积与之相同的金属块B, 金属块B浸没在液体内, 而木块漂浮在液面上, 液面正好与容器口相齐. 某瞬间细线突然断开, 待稳定后液面下降了h1; 然后取出金 属块B, 液面又下降了h2; 最后取出木块A, 液面又下降了h3. 则木块A与金属块B的密度之比为 .
(模块二: 船球模型之测量密度模型)
一个底面积为50 cm2的烧杯装有某种液体, 将一个木块放入烧杯的液体中, 木块静止时液体深h1=10cm, 如图甲所示; 把一个小石块放在木块上, 液体深h2=16cm, 如图乙所示; 若将小石块放入液体中, 液体深h3=12cm, 如图丙所示, 石块对杯底的压力F=1.6N. 则小石块的密度ρ石为 kg/m3.(g取10N/kg)
2.4×103 (模块二: 船球模型之测量密度模型)
一根轻质小弹簧原长10厘米, 两端分别连接在容器底部和物体A上, 将水逐渐注入容器, 当物体的一半浸入水中时, 弹簧长12cm, 如图(a) 所示. 把水倒出, 改用密度为 0.8×103kg/m3的油注入容器, 当物体A全部浸入油中时, 弹簧长15cm, 如图(b) 所示. 前后两种情况下物体受到的浮力之比为_________; 物体A的密度为_________kg/m3.
5:8 0.3×103 (模块三: 含有弹簧的浮力问题)
船上载着许多钢材, 此时甲板离水面的高度为; 把这些钢材都放在水中用绳悬挂于船下, 此时甲板离水面的高度为, 则与相比较 ( )
A. B. C. D. 无法比较
C
如图所示, 将物块投入漂浮于水面的小烧杯中, 小烧杯杯底距液面高度h1为25cm; 将物块取出后系在烧杯底并静止后, 小烧杯杯底距液面高度变为h2大小为20 cm; 剪断细绳后物块掉入杯底, 此时小烧杯底距水面距离变为h3大小为5cm; 则物块的密度为 .
4×103kg/m3
小芳同学在实验室测量某种液体的密度. 实验桌上的器材有: 一把刻度尺、一个厚底平底试管(试管壁厚度不计) 和一个装有适量水的水槽.
⑴ 她的测量步骤如下:
① 将厚底平底试管放入水槽内水中, 试管竖直漂浮在水面上. 用刻度尺测出试管底到水槽中水面的高度h1, 如图甲所示;
② 将适量的待测液体倒入试管中, 试管仍能竖直漂浮在水面上. 用刻度尺测出试管底到水槽中水面的高度h2和试管内液柱的高度h3, 如图乙所示.
⑵ 请你帮助小芳写出计算待测液体密度的表达式?液==????????.
如图所示, 质量为540g的凹形铝槽, 放入底面积为100cm2的圆柱形容器中的液体中, 铝槽浮在液面上, 槽口恰好与液面相平, 这时液面上升了2.7cm. 若使铝槽沉入液体中, 则沉入前后液体对容器底部的压强变化△p= Pa.
(已知ρ铝=2.7×103 kg/m3 , g=10N/kg)
140
如图所示, 用质量不计、长度为10cm的弹簧将正方体物块下表面与底面积为150cm2的圆柱形容器底部相连, 正方体物块竖直立于圆柱形容器内, 且不与容器壁接触, 弹簧的长度缩短为2cm; 现向容器内部倒入水, 当物块有1/5的体积露出水面时, 弹簧的长度又恢复到原长; 现继续向容器内倒入0.2kg的水后(水不溢出), 容器底部所受水的压强为 __________Pa. 已知: 弹簧的长度每改变1cm时, 所受力的变化量为1N, 取g=10N/kg.
2000
(多选) 一个漂浮在小型游泳池水面上的小船, 一个人从池水中捞出以下几种物体放入船中, 其中能使池中水面升高的是 ( )
A. 从池中捞铁块 B. 从水面上捞木块
C. 从池中捞石块 D. 将池中的一些水装入船中
AC
如图所示, 大杯中盛有液体, 装有密度均匀小球的小杯漂浮在液面上, 如果将小球取出并投入液体中, 液体的液面一定 ( )
A. 上升 B. 下降
C. 不变 D. 下降或不变
D
水槽中放一个小铁盒, 铁盒中放少许细线和一个铝块, 铁盒漂浮在水面. 现用细线把铝块拴在铁盒下面, 铁盒仍漂浮在水面, 如图所示; 讨论此时水槽中的水位以及铁盒浸入水中的体积, 说法正确的是 ( )
A. 水槽中水位不变, 铁盒浸入水中的体积变大
B. 水槽中水位下降, 铁盒浸入水中的体积不变
C. 水槽中水位上升, 铁盒浸入水中的体积不变
D. 水槽中水位不变, 铁盒浸入水中的体积变小
D
一、测密度模型
1、测质量模型(漂浮法)
① mg=ρ液gS1(H2-H1) 条件: 外容器需直上直下
② mg=ρ液gS2(h2-h1) 条件: 内容器需直上直下
2、测体积模型
① 排水法: V球=(H4-H3) S1
② 悬挂法: V球=(h3-h4) S2
有一底面积为S的圆柱形容器中装有适量的水, 有一平底小试管漂浮在水中, 此时液面的高度为H?, 将一物块系在平底试管底部, 一起漂浮于水中, 此时液面高度为H?, 剪断细线, 物块沉底, 此时液面高度为H?, 则物块密度ρ=________________.
如图所示, 若h?、h?、h?已知, 大容器中装的液体是水, 已知小容器底面积S?, 则物块的密度为ρ=_____________________.
小华家里有一个金属球, 不知道是用何种金属制成的, 因此她决定用学过的物理知识测出金属球的密度. 由于身边没有测量质量的工具, 因此她找来了圆柱形容器、刻度尺和一个塑料小碗. 把圆柱形容器放在水平桌面上并在其中装入适量的水, 让塑料小碗漂浮在水面上, 此时容器内的水深为18cm. 当把金属球放入容器内的水中时, 容器内的水深为19.5cm, 如图甲所示. 现将金属球取出后放入塑料小碗中静止时, 如图乙所示. 乙图中的水面比甲图中的水面高3cm. 已知: 容器的内部底面积为400cm2. 则金属球的密度是 kg/m3.
3×103
圆柱形容器中装有适量的水, 将一只装有配重的薄壁长烧杯放入圆柱形容器的水中, 烧杯静止时容器中水的深度 H1为20cm , 如图甲所示. 将金属块 A 吊在烧杯底部, 烧杯静止时露出水面的高度 h1为 5cm , 容器中水的深度H2为35cm , 如图乙所示. 将金属块A放在烧杯中, 烧杯静止时露出水面的高度h2为1cm , 如图丙所示. 已知圆柱形容器底面积为烧杯底面积的2倍. 则金属块A的密度为________kg/m3.
如图所示, 柱形容器中装有密度为ρ1=1.2g/cm3的某种液体, 将一金属块放入底面积为S=100cm2的长方体塑料盒中, 塑料盒竖直漂浮在液面上, 且液体不会溢出容器, 其浸入液体的深度为h1=20cm. 若把金属块从塑料盒中取出, 用细线系在塑料盒的下方, 放入该液体中, 塑料盒竖直漂浮在液面上, 且金属块不接触容器底, 塑料盒浸入液体的深度为h2=15cm. 剪断细线, 金属块沉到容器底部, 塑料盒仍竖直漂浮在液面上, 其浸入液体的深度为h3=10cm. 则金属块的密度ρ2= g/cm3.
2.4
小明用装有适量水的薄壁小试管、螺母和细线制成一个测量小石块密度的装置. 将此装置放入水中静止时, 试管露出水面的高度h1为5cm, 如图甲所示; 在试管中轻轻放入小石块, 此装置在水中静止时, 试管露出水面的高度h2为2cm, 如图乙所示. 已知小石块放入试管前后, 试管中的液面差h3为2cm. 则石块的密度为
kg/m3.
3×103
液体压强变化量
① 投球: 液体对槽底
② 剪绳: 液体对槽底
如图所示, 在底面积为S的圆柱形水池底部有一个金属球(球与池底没有密合) , 圆柱型的水槽漂浮在池内的水面上, 此时水槽受到的浮力为F1. 若把金属球从水中捞出并放在水槽中漂浮在水池中, 此时水槽受到的浮力为F2, 捞起金属球前、后水池底受到水的压强变化量为p, 水的密度为ρ水. 根据上述条件可以求出 ( )
A. 金属球受的重力为F2 –F1–pS
B. 金属球被捞起前受的浮力为F2 –F1
C. 金属球被捞起前、后水槽底受水的压力减小了pS
D. 金属球被捞起前、后水槽排开水的体积增大了
D
如图所示, 将一个木块投入装有液体的水槽中, 处于漂浮状态, 现用大小为4N的力竖直向下压, 此时液体对水槽底部压强增大了. 又找来一个金属块用细线挂在木块的下面, 这时液面深度为; 剪断细线, 金属块下沉, 稳定后液面深度降低为, 金属块对水槽底部压力大小为3.2N, 求: 剪断后, 液体对水槽底部压强减少了多少? 液体密度为多少? ()
;
一冰块内冰封一合金物体, 将其放入盛有适量水, 底面积为的烧杯内, 正好悬浮在水中, 此时烧杯内的水对烧杯底的压强增加了; 当冰完全熔化后, 水对烧杯底的压强又变化了. 忽略烧杯内水的体积所受温度的影响, 当冰完全熔化后, 烧杯底对合金物体的支持力是 N. (冰的密度为, 取) .
0.44
如图所示, 底面积为200cm2的容器底部有一固定轻质弹簧, 弹簧上方连有一边长为10cm的正方体木块A, 当容器中水深为20cm时, 木块A有的体积浸在水中, 此时弹簧恰好处于自然状态, 没有发生形变. 向容器内缓慢加水, 当弹簧伸长了1cm时停止加水, 此时弹簧对木块拉力为1N. 加水前后容器底部受到水的压强变化了 Pa. (不计弹簧受到的浮力, g取10N/kg)
200
如图所示, 将挂在弹簧测力计下端高为8cm、横截面积为100cm2的柱形物块缓慢放入底面积为500cm2的圆柱形容器内的水中. 当物块直立静止时, 物块浸入水中深度为2cm, 弹簧测力计的示数为8N, 水对容器底部的压强为1.2×103Pa. 现向容器中加水, 当弹簧测力计的示数为5N时, 注入水的质量为m, 水对容器底部的压强为p, 柱形物块受到的浮力为F. 已知弹簧测力计的称量范围为0~10N, 刻度盘上0~10N刻度线之间的长度为10cm. 若g取10N/kg, 则下列说法中正确的是( )
A. 柱形物块所受重力大小为8N
B. 柱形物块受到的浮力F大小为3N
C. 水对容器底部的压强p为1.8×103Pa
D. 向容器中注入水的质量m为3.0kg
C
实验桌上有如图所示的下列器材, 请你利用这些器材, 测出小金属块的密度. 写出实验步骤(用字母表示测出的物理量, 水的密度用ρ水表示)及金属块的密度表达式.
实验步骤:
(1) 让小容器漂浮在水槽中的水面上, 量出这时水面到槽边沿的距离h1.
(2) 量出 , 量出这时水面到槽上边沿的距离h2.
(3) 将金属块从小容器中取出用细线系住没入槽内水中, 量出这时水面到槽上边沿的距
离h3. 金属块密度的表达式 金属 =
(2) 将小金属块放入漂浮在水面上的小容器内
(3)
爱好科技的小刚自己制作了一条小木船, 船上带有金属船锚, 船舷上表明了三种情况的排水量.
(1) 将锚放在船舱里, 当船静止在水槽中时观察对应的排水量为;
(2) 用细线拴住船锚, 悬挂在船下方的水中且完全浸没, 观察对应的排水量为, 此时水槽中的水面将 ; (选填“升高”、“降低”或“不变”) .
(3) 把细线放得更长些, 直至线松了, 锚沉在盆底, 记下此时对应的排水量为于是利用这些排水量测出了船锚的密度. 则锚的密度 .
不变; ρ水
实验桌上有如下器材: 细长平底试管一支(已知底面积为S)、小汤匙一个、抹布一块、刻度尺一把、大水槽一个(水槽的深度大于平底试管的高度)、足量的水、足量的细沙子、天平及配套砝码. 要求从实验桌上选择适当的器材, 设计一个实验证明: 在同种液体中, 固体所受的浮力大小跟排开液体的体积成正比. 要求: 写出主要的实验步骤并设计记录实验数据的表格.
(1) 把天平放在水平桌面上, 调节天平平衡; (有此项给1分, 没有扣1分).
(2) 用刻度尺测出试管的长度L并记录;
(3) 用药匙取适量的细沙装入试管, 用天平测出细沙和试管的总质量m1; 再将试管放入盛有水的水槽中, 使试管竖直漂浮在水面上静止, 用刻度尺测出试管露出水面的高度h1; 将m1、h1记录在表格内.
(4) 用抹布擦干试管, 用药匙再取适量的细沙装入试管, 用天平测出细沙和试管的总质量m2; 再将试管放入盛有水的水槽中, 使试管竖直漂浮在水面上静止, 用刻度尺测出试管露出水面的高度h2; 将m2、h2记录在表格内.
(5) 仿照步骤(4)再做4次实验, 测出细沙和试管的总质量m3、m4、m5、m6; 测出每次试管露出水面的高度h3、h4、h5、h6, 并将数值记录在表格内.
(6) 计算出每次试管浸入水中的深度(L-h)和排开水的体积V排=(L-h)S; 将数据记录在表管内.
(7) 根据物体漂浮时F浮=G物=mg, 可知试管每次漂浮时所受的浮力F浮.
(8) 分析F浮和试管排开水的体积V排确定两者的关系.
S=
实验次数
试管的长度L/cm
细沙和试管的总质量m/kg
重力G/N
试管露出水面高度h/cm
试管浸入水中深度(L-h)/cm
试管排开水的体积V排/cm3
浮力F浮/N
如图所示, 在盛有某种液体的圆柱形容器内放有一木块A, 在木块的下方用轻质细线悬挂一体积与之相同的金属块B, 金属块B浸没在液体内, 而木块漂浮在液面上, 液面正好与容器口相齐. 某瞬间细线突然断开, 待稳定后液面下降了h1; 然后取出金 属块B, 液面又下降了h2; 最后取出木块A, 液面又下降了h3. 则木块A与金属块B的密度之比为 .
(模块二: 船球模型之测量密度模型)
一个底面积为50 cm2的烧杯装有某种液体, 将一个木块放入烧杯的液体中, 木块静止时液体深h1=10cm, 如图甲所示; 把一个小石块放在木块上, 液体深h2=16cm, 如图乙所示; 若将小石块放入液体中, 液体深h3=12cm, 如图丙所示, 石块对杯底的压力F=1.6N. 则小石块的密度ρ石为 kg/m3.(g取10N/kg)
2.4×103 (模块二: 船球模型之测量密度模型)
一根轻质小弹簧原长10厘米, 两端分别连接在容器底部和物体A上, 将水逐渐注入容器, 当物体的一半浸入水中时, 弹簧长12cm, 如图(a) 所示. 把水倒出, 改用密度为 0.8×103kg/m3的油注入容器, 当物体A全部浸入油中时, 弹簧长15cm, 如图(b) 所示. 前后两种情况下物体受到的浮力之比为_________; 物体A的密度为_________kg/m3.
5:8 0.3×103 (模块三: 含有弹簧的浮力问题)
船上载着许多钢材, 此时甲板离水面的高度为; 把这些钢材都放在水中用绳悬挂于船下, 此时甲板离水面的高度为, 则与相比较 ( )
A. B. C. D. 无法比较
C
如图所示, 将物块投入漂浮于水面的小烧杯中, 小烧杯杯底距液面高度h1为25cm; 将物块取出后系在烧杯底并静止后, 小烧杯杯底距液面高度变为h2大小为20 cm; 剪断细绳后物块掉入杯底, 此时小烧杯底距水面距离变为h3大小为5cm; 则物块的密度为 .
4×103kg/m3
小芳同学在实验室测量某种液体的密度. 实验桌上的器材有: 一把刻度尺、一个厚底平底试管(试管壁厚度不计) 和一个装有适量水的水槽.
⑴ 她的测量步骤如下:
① 将厚底平底试管放入水槽内水中, 试管竖直漂浮在水面上. 用刻度尺测出试管底到水槽中水面的高度h1, 如图甲所示;
② 将适量的待测液体倒入试管中, 试管仍能竖直漂浮在水面上. 用刻度尺测出试管底到水槽中水面的高度h2和试管内液柱的高度h3, 如图乙所示.
⑵ 请你帮助小芳写出计算待测液体密度的表达式?液==????????.
如图所示, 质量为540g的凹形铝槽, 放入底面积为100cm2的圆柱形容器中的液体中, 铝槽浮在液面上, 槽口恰好与液面相平, 这时液面上升了2.7cm. 若使铝槽沉入液体中, 则沉入前后液体对容器底部的压强变化△p= Pa.
(已知ρ铝=2.7×103 kg/m3 , g=10N/kg)
140
如图所示, 用质量不计、长度为10cm的弹簧将正方体物块下表面与底面积为150cm2的圆柱形容器底部相连, 正方体物块竖直立于圆柱形容器内, 且不与容器壁接触, 弹簧的长度缩短为2cm; 现向容器内部倒入水, 当物块有1/5的体积露出水面时, 弹簧的长度又恢复到原长; 现继续向容器内倒入0.2kg的水后(水不溢出), 容器底部所受水的压强为 __________Pa. 已知: 弹簧的长度每改变1cm时, 所受力的变化量为1N, 取g=10N/kg.
2000
