2018--2019学年八年级物理下册 第十章 浮力_变化量 讲义 新版新人教版
文档属性
| 名称 | 2018--2019学年八年级物理下册 第十章 浮力_变化量 讲义 新版新人教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-03-21 00:00:00 | ||
图片预览


文档简介
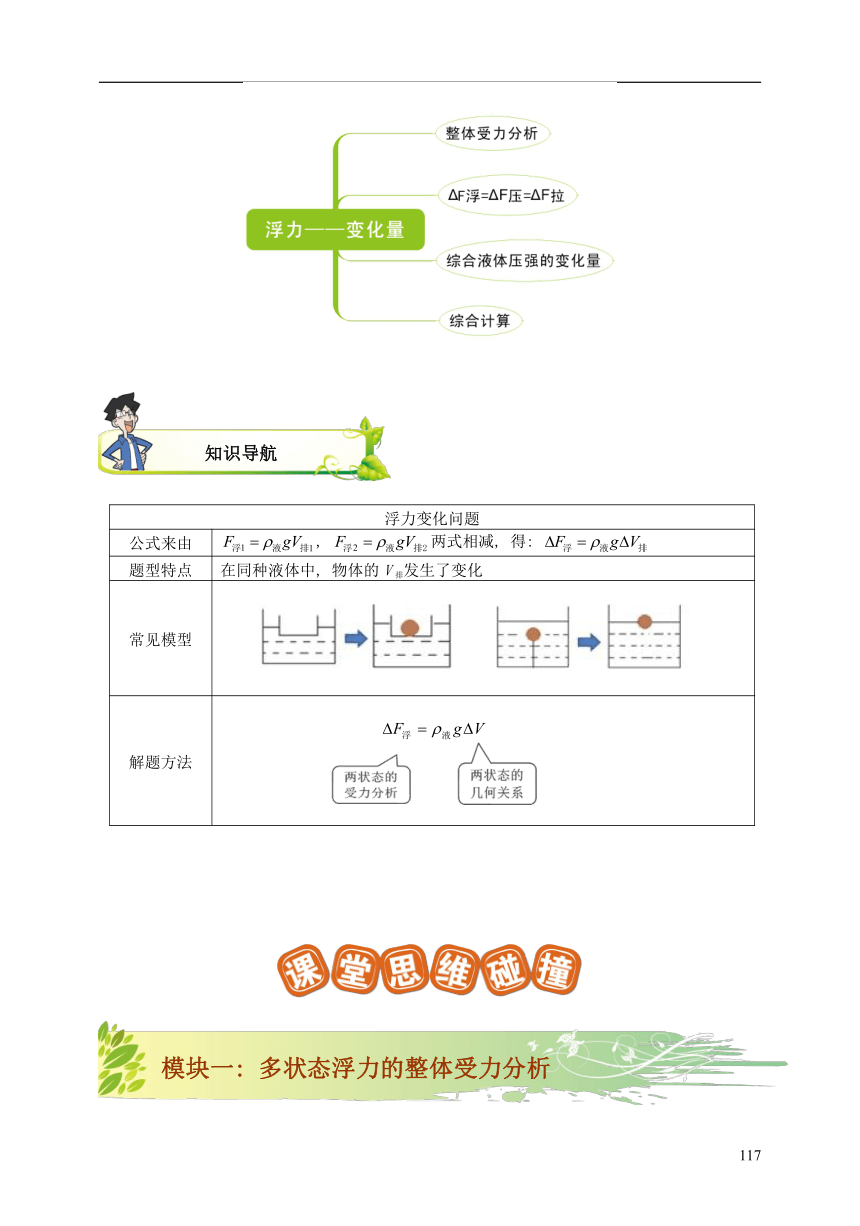
浮力——变化量
浮力变化问题
公式来由
, 两式相减, 得:
题型特点
在同种液体中, 物体的V排发生了变化
常见模型
解题方法
如图所示, 将重为G 的金属小球用细线系好, 浸入盛水的烧杯中(烧杯中的水没有溢出), 金属小球受到的浮力为F浮, 杯底增加的压力为△F1; 如将此金属小球直接投入水中, 杯底增加的压力为△F2, 则下列关系式中正确的是( )
A. △F2-△F1= F浮
B. △F2+△F1= G
C. △F2: △F1=F浮: G
D. △F2: △F1= G : F浮
D
小东将装有适量水的水杯放在台秤的托盘上, 台秤的示数为0.6kg. 他又将一个用细线拴住的石块浸没在水中静止, 如图所示, 台秤的示数为0.8kg. 小东把石块放置在杯底并放手后, 台秤的示数为1.1kg. 由此可知石块的密度为 kg/m3.
2.5×103
水平桌面上放有甲、乙、丙、丁四个完全相同的圆柱形容器, 容器内分别盛有等质量的液体. 其中甲、乙、丁容器中的液体密度相同. 若将小球A放在甲容器的液体中, 小球A静止时漂浮, 此时甲容器对桌面的压力为F1; 若将小球A用一段不计质量的细线与乙容器底部相连, 并使其浸没在该容器的液体中, 小球A静止时乙容器对桌面的压力为F2; 若将小球A放在丙容器的液体中, 小球A静止时悬浮, 此时丙容器对桌面的压力为F3; 若将小球A放在丁容器的液体中, 用一根不计质量的细杆压住小球A, 使其浸没, 且不与容器底接触, 小球A静止时丁容器对桌面的压力为F4. 则下列判断正确的是 ( )
A. F2
☆ 思考题: 木块的, 需用多大的力才能将其压入水中? ( )
“可以推出1N浮力对应的”.
☆ 已知绳子拉力为T, 剪断绳子后木球露出水面的体积为多少?
解析:
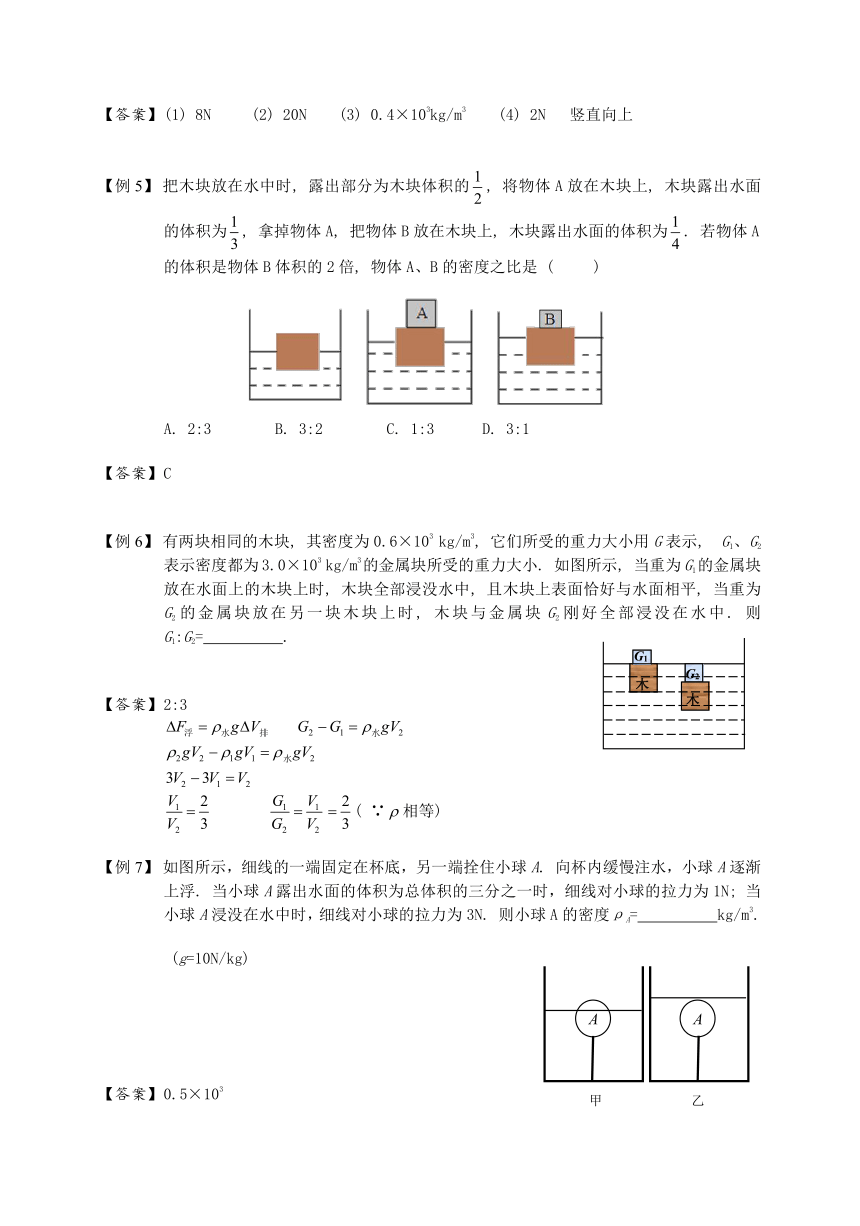
如图所示, 将一个质量为0.8kg的木块A放在水中漂浮, 若给木块施加一个竖直向下大小为12N的压力F1, 木块刚好能浸没在水中并静止. ( g=10N/kg) 求:
(1) 木块受到的重力G木
(2) 此时木块受到的浮力F浮
(3) 木块的密度ρ木
(4) 若施加一个竖直方向的力F2, 刚好使木块3/10 的体积浸没在水中并静止, 求F2的方向和大小
(1) 8N (2) 20N (3) 0.4×103kg/m3 (4) 2N 竖直向上
把木块放在水中时, 露出部分为木块体积的, 将物体A放在木块上, 木块露出水面的体积为, 拿掉物体A, 把物体B放在木块上, 木块露出水面的体积为. 若物体A的体积是物体B体积的2倍, 物体A、B的密度之比是 ( )
A. 2:3 B. 3:2 C. 1:3 D. 3:1
C
有两块相同的木块, 其密度为0.6×103 kg/m3, 它们所受的重力大小用G表示, G1、G2表示密度都为3.0×103 kg/m3的金属块所受的重力大小. 如图所示, 当重为G1的金属块放在水面上的木块上时, 木块全部浸没水中, 且木块上表面恰好与水面相平, 当重为G2的金属块放在另一块木块上时, 木块与金属块G2刚好全部浸没在水中. 则G1:G2= .
2:3
( ∵相等)
如图所示,细线的一端固定在杯底,另一端拴住小球A. 向杯内缓慢注水,小球A逐渐上浮. 当小球A露出水面的体积为总体积的三分之一时,细线对小球的拉力为1N; 当小球A浸没在水中时,细线对小球的拉力为3N. 则小球A的密度ρA= kg/m3.
(g=10N/kg)
0.5×103
如图所示的木块浸没在水中, 细线对木块的拉力是2N. 剪断细线, 待木块A静止后, 将木块露出水面的部分切去, 再在剩余的木块上加1N向下的压力时, 木块有20cm3的体积露出水面, 则木块的密度约为 kg/m3. ( g取10N/kg)
0.6×103
将塑料球和泡沫球用细线相连放入水中时, 泡沫球露出水面的体积为它自身体积的一半, 如图所示. 把细线剪断后, 塑料球沉底, 泡沫球露出水面的体积为自身体积的, 已知塑料球与泡沫球的体积之比为1:8, 则塑料球的密度为
kg/m3.
3×103
一个竖直放置在水平桌面上的圆柱形容器内装密度为的液体. 将挂在弹簧测力计下的金属块A 浸没在该液体中( A与容器底未接触) ,金属块A 静止时,弹簧测力计的示数为F,将木块B 放入该液体中,静止后木块B露出液面的体积与其总体积之比为7 : 12 ; 把金属块A 放在木块B 上面,木块B 刚好没入液体中(如图所示) . 若已知金属块A 的体积与木块B 的体积之比为13 : 24 ,则金属块A 的体积为_________.
当A浸入液体中时有: ;
根据,,又因为.
解得.
公式推导
如图所示的容器, 上部横截面积为, 底部横截面积为, 容器上下两部分高分别为, 容器中盛有某种液体, 有一个空心金属球用细绳系住, 绳的另一端栓在容器底部, 此时球全部浸没在液体中, 位置如图, 绳对球的拉力为, 如将细绳剪断, 待空心金属球静止后液体对容器底部的压力减少了 . ( 用题中字母表示)
底面积为50cm2的平底圆柱形容器内盛满某种液体后, 放置于水平桌面的中央(容器壁厚度不计), 已知液体的压强与深度的关系如左图所示. 现用轻质细线提起一个质量为80g的实心球缓慢浸没于容器内的液体中, 如右图所示, 待球静止后, 擦干容器外壁, 已知细线给球的拉力为0.5N, 剪断细线, 实心球下沉到容器底部, 此时容器对桌面的压强比只盛满液体容器对桌面的压强增大了 pa.( g取10 N//kg)
100
底面积为100cm2的烧杯中装有适量水. 当金属块浸没在水中静止时, 如图(甲) 所示, 弹簧测力计的示数F1=3.4N, 水对杯底的压强为p1; 当金属块总体积的1/4露出水面静止时, 如图(乙) 所示, 弹簧测力计的示数为F2, 水对杯底的压强为p2; 若p1、p2之差为50Pa, g取10N/kg. 则下列判断中正确的是 ( )
A. 金属块的体积V金为 2 ×10-3m3
B. 金属块的密度为
C. 金属块的重力G为4.5N
D. 弹簧测力计的示数F2为2.9N
B
此题可以拓展提问金属块的密度=? ()
装有水的圆柱形容器的底面积为S. 将一木块放入水中, 木块漂浮, 水未溢出, 容器底受到水的压强增大了p1. 把木块浸入水中的部分削掉, 并把原露出水面的部分在放回水中, 木块静止后, 容器底受到水的压强比木块被削掉前减小了p2. 则木块原来的体积V= .
在甲、乙两个完全相同的圆柱形容器内装有质量相等的水. 现将A、B两个实心物块分别放入甲、乙两个容器中, 物理均可浸没且水不溢出容器. 已知A、B两物块的密度分别为, , 两物块的质量关系为. A、B两物块的体积, 分别为VA和VB, A、B两物块浸没在水中所受浮力分别为FA、FB, 物块在水中静止时两容器底部对两物块的支持力分别为NA、NB, 放入物块前、后, 两容器底部受到水的压强增加量分别为, 放入物块后, 桌面受到甲、乙两容器的压力增加量分别为.则下列四项判断中正确的是 ( )
A.
B.
C.
D.
D
本题对压力、压强变化量的理解考查较深.
根据质量与密度的比例关系, 得到 . 所以
所以D正确.
在图中, 底面积为S=100cm2的圆柱形容器中装有密度为ρ的某种液体, 图甲中, 液体的深度是20cm, 此时手对细线的拉力是8 N, 物体A对容器底部的压力是F1; 图乙中, 手对细线的拉力是15N, 液体对容器底部的压强为p; 图丙中, 物体A露出液面的体积是总体积的五分之二, 液体对物体A下表面的压力是F2, 液体的深度是16cm, 手对细线的拉力是19.8N, (g取10N/kg)以下说法正确的是 ( )
A. F1 =6N B. ρ= 1.0×103kg/m3
C. P=2.4×103 Pa D. F2 = 12N
C
将甲、乙两个完全相同的溢水杯放在水平桌面上, 甲溢水杯中装满密度为ρ1的液体, 乙溢水杯中装满密度为ρ2的液体, 如图甲所示, 将密度为ρA, 重为GA的物块A轻轻放入甲溢水杯中, 物块A漂浮在液面上, 并且有1/4的体积露出液面, 液体对甲杯底的压强为p1, 如图乙所示, 将密度为ρB, 重为GB的物块B轻轻放入乙溢水杯中, 物块B沉底, 物块B对乙溢水杯底的压力为F, 液体对乙溢水杯杯底的压强为p2, 已知ρ1: ρ2=3: 2, ρA: ρB=4: 5, 则下列说法中正确的是 ( )
A. ρ1: ρA=3: 4
B. FA浮: FB浮=9: 8
C. p1: p2=2: 3
D. F: GB=13: 45
D
放在水平桌面上的圆柱形容器中装有适量的水. 现将一木块B放入水中, 木块漂浮, 木块静止时有2/5的体积露出水面, 如图甲所示. 将一金属块A在木块B上, 木块恰好浸没在水中, 如图乙所示; 若将金属块A放入某种液体中中, 容器底对金属块的支持力是3N, 如图丙所示. 已知: 木块B的质量是810g, 金属块A的体积为200cm3, 则某种液体的密度为 kg/m3 (g取10N/kg).
1.2×103
放在水平桌面上的甲、乙两个圆柱形容器中分别盛有密度为ρ1、ρ2的液体. 物体A、B是两个实心正方体, 密度分别为ρA、ρB, 所受的重力分别为GA、GB, 体积分别为VA、VB. 将物体A和B以不同的方式先后放入甲、乙两容器的液体中, 如图所示. 在甲容器中, B叠放在A上, A有1/3的体积露出液面, 液体对容器底的压力比未放入物体时增大了ΔF甲. 在乙容器中, A、B通过细绳相连, B受到容器底的支持力为(B与容器底不密合) , 受到细绳的拉力为F拉, 液体对容器底的压力比未放入物体时增大了ΔF乙. 不计细绳的质量和体积, 已知ρ1: ρ2=2: 1, VA: VB =27: 8, F支: F拉=1: 21, 下列判断中正确的是 ( )
A. ρA: ρB=8: 135, ΔF甲:ΔF乙=1:1
B. ρA: ρB=8: 135, ΔF甲:F支=35: 1
C. ρA: ρ1=1: 9, F拉:GA=2: 7
D. ρB: ρ2=15: 4, F拉:GB=7: 10
D
水平桌面上放有甲、乙、丙、丁四个完全相同的圆柱形容器, 容器内分别盛有等质量的液体. 其中甲、乙、丁容器中的液体密度相同. 若将小球放在甲容器的液体中, 小球静止时漂浮, 此时液体对甲容器底的压强为; 若将小球用一段不计质量的细线与乙容器底部相连, 并使其浸没在该容器的液体中, 小球静止时液体对容器底的压强为; 若将小球放在丙容器的液体中, 小球静止时悬浮, 此时液体对容器底的压强为; 若将小球放在丁容器的液体中, 用一根不计质量的细杆压住小球, 使其浸没, 且不与容器底接触, 小球静止时液体对容器底的压强为. 则、、和的关系是 ( )
A. B.
C. D.
A
如图甲所示, 一个木块的密度为, 用细线将木块与容器底部连在一起, 当木块完全浸没在水中时, 细线对木块的拉力是1N; 若剪断细线, 待木块静止后, 将木块露出水面的部分切去, 再在剩余的木块上加向下的压力时, 如图乙所示, 则木块有 的体积露出水面. ( 取)
15
如图所示的容器, 上部横截面积为S1=100cm2, 中间部分横截面积为S2=200cm2, 底部横截面积为S3=150cm2 , 容器上中下三部分高都为 h, 且h=20cm, 容器中盛有某种液体, 有一个空心金属球用细绳系住, 绳的另一端栓在容器底部, 此时球全部浸没在液体中, 位置如图, 绳对球的拉力为=5N, 如将细绳剪断, 待空心金属球静止后液面高度大于2h, 则液体对容器底部的力减少了 .
7.5N
盛有液体的圆柱形容器置于水平桌面上, 如图甲所示, 容器对桌面的压强为500Pa; 用细线拴一金属球, 将金属球浸没在液体中, 如图乙所示, 容器对桌面的压强为600Pa; 将细线剪断, 金属球沉到容器底部, 如图丙所示, 容器对桌面的压强为1500Pa. 已知: 容器的底面积为100cm2, 金属球的密度为8g/cm3, g取10N/kg. 则下列判断正确的是( )
A. 金属球所受浮力是6N
B. 金属球的体积是100cm3
C. 液体的密度是0.8 g/cm3
D. 金属球对容器底部的压力是10N
C
边长为1dm的正方体木块, 漂浮在酒精液面上时, 有一半的体积露出液面, 如图甲所示. 将木块从底部切去一部分, 粘上体积相同的玻璃后, 放入某种液体中, 它仍漂浮在液面上, 如图乙所示. 此时液体对它竖直向上的压强为980Pa. 已知酒精的密度为0.8×103 kg/m3, 玻璃的密度为2.4×103 kg/m3, 粘玻璃所用胶的质量和体积均忽略不计, 则所粘玻璃的质量为 kg.
0.72
如图所示, 质量为100g底面积为正方形的木块静止在水平地面上, 其底面积大小为1×10?2m2, 将底面积为5×10?3m2的圆柱形轻质容器置于木块中央, 且容器内盛有400g的水. 此时水平地面上受到的压力为F, 水对容器底部的压强为p; 若再将密度为ρ物的物块放入水中如图所示, 物块沉底且水不溢出, 此时水对容器底部产生的压强的增加量与水平地面受到压强的增加量相等, 则下列结果正确的是( )
A. F=3.92N p=784 Pa
B. F=3.92N ρ物 =2.0×103kg/m3
C. p =784 Pa ρ物 =4.0×103kg/m3
D. p=784 Pa ρ物 =2.0×103kg/m3
D
