江西省上饶市广丰一中2018-2019学年度下学期期初考试高一数学试卷
文档属性
| 名称 | 江西省上饶市广丰一中2018-2019学年度下学期期初考试高一数学试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 306.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-21 18:14:14 | ||
图片预览



文档简介
广丰一中2018-2019学年度下学期期初试卷
高一数学试卷
一、单选题
1、已知集合M={x|},N={y|,x∈R},则M∩N=( )
A.? B. {x|x≥1} C.{x|x>1} D.{x| x≥1或x<0}
2、下列函数中,既是偶函数又在区间(-∞,0)上单调递减的是( )
A. B. C. D.
3、若过两点的直线的倾斜角为,则( )
A. B. C.3 D.-3
4、设,是条不同的直线,是一个平面,以下命题正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
5、若点P(3,4)和点Q(a,b)关于直线对称,则( )
A., B.,
C., D.,
6、已知函数,则
A.1 B. C.2019 D.
7、已知函数,则不等式的解集为( )
A. B. C. D.
8、已知为定义在上的奇函数,,且对任意的时,当时,则不等式的解集为( )
A. B. C. D.
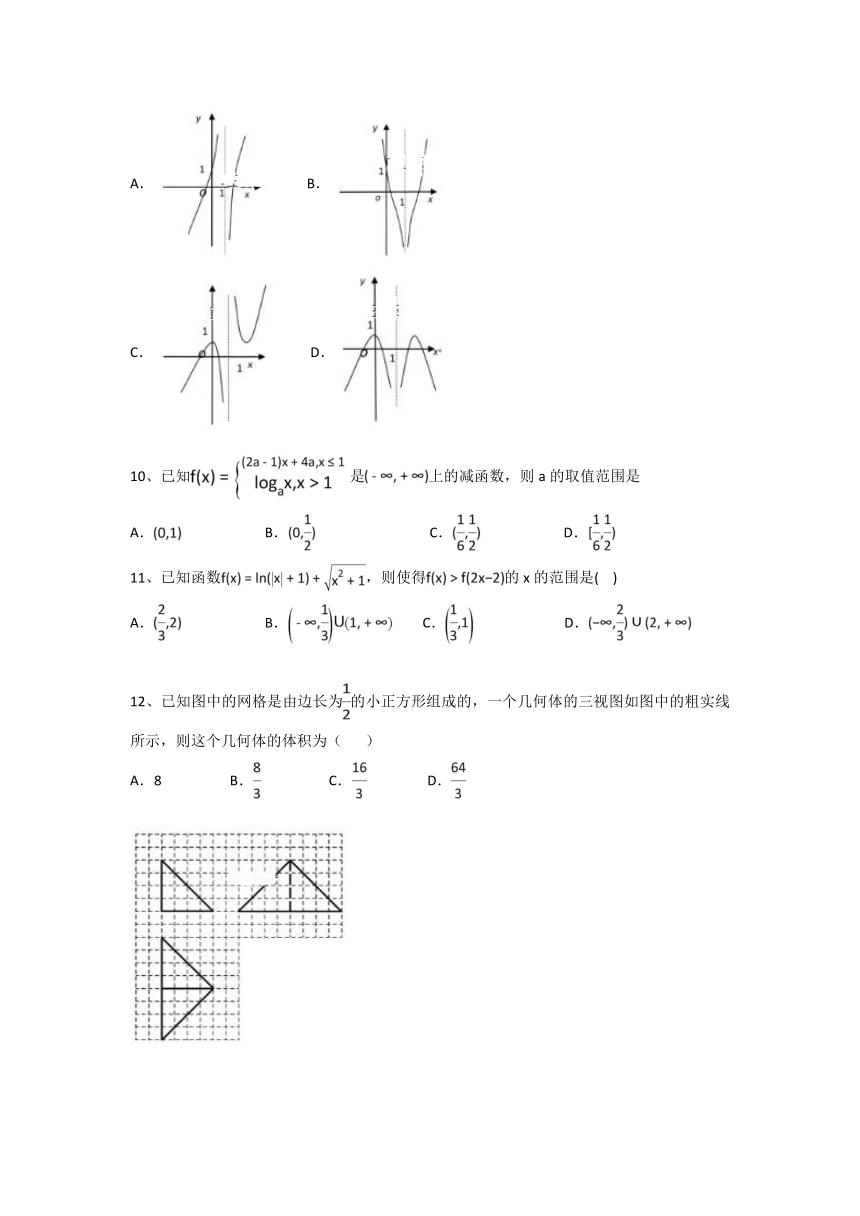
9、函数的图象大致为( )
A. B.
C. D.
10、已知是上的减函数,则a的取值范围是
A. B. C. D.
11、已知函数,则使得的x的范围是(????)
A. B. C. D.
12、已知图中的网格是由边长为的小正方形组成的,一个几何体的三视图如图中的粗实线所示,则这个几何体的体积为( )
A.8 B. C. D.
二、填空题
13、函数的零点是____________.
14、如图,平面,,,,,分别为的中点,则三棱锥的体积为________.
15、已知直线与直线互相垂直,则实数=________.
16、一个四棱锥的俯视图如图所示,它的外接球的球心到底面的距离是该球半径的一半,则这个四棱锥的侧视图的面积为______.
三、解答题
17、(10分)计算下列各式:
(1);
(2).
18、(12分)已知R为实数集,集合A={x|1(1)求集合B,
(2)若A∩C=C,求实数m的取值范围
19、(12分)已知直线 ,
(Ⅰ)若,求实数的值;
(Ⅱ)当时,求直线与之间的距离.
20、(12分)已知函数,.
(1)当时,求的值域;
(2)设的最小值为,请写出的表达式,并求的解.
21、(12分)如图,在四棱锥中,底面是矩形,平面,且,,点为线段的中点.
(Ⅰ)求证:平面;
(Ⅱ)求证:;
(Ⅲ)求三棱锥的体积.
22、(12分)已知函数其中
(1)解关于的不等式;
(2)若函数在区间上的值域为,求实数的取值范围;
(3)设函数,求满足的的集合。
广丰一中2018-2019学年度下学期期初考试高一数学参考答案
一、单选题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
D
D
A
D
D
C
B
D
A
B
二、填空题
13、1或-4 14、 15、0 16、
三、解答题
17.解(1)原式==-5.…………………….5分
(2)原式=……………………….10分
18、解(1)由得,所以…………3分
因为,,
所以. …………………6分
(2)因为,所以,分两种情况讨论,
当时,由,解得 …………………8分
当时,由此不等式组无解,……………10分
故实数的取值范围是………………………………………………12分
19、解(Ⅰ)由l1⊥l2可得:a+3(a﹣2)=0,
解得;……………………………………..6分
(Ⅱ)当l1∥l2时,有,
解得a=3,……………………………………..8分
此时,l1,l2的方程分别为:3x+3y+1=0,x+y=0即3x+3y=0,………………10分
故它们之间的距离为.……………………………………………..12分
20、 解(1)时,开口向上,对称轴为,
在上为减函数,在上为增函数,
的值域为. ……………4分
(2)时,即时,在上为增函数,
,…………………………………………6分
时,即时,在上为减函数,在上为增函数,
…………………………………………………………………8分
时,即时,在上为减函数,
……………………………………………………………………….10分
时,或
时,或
综上所述:t=-2或t=4………………………………………….………………..12分
21、解(Ⅰ)证明:连接,交于点,连接,
因为是矩形对角线交点,所以为中点,
又已知为线段的中点,所以,又平面
平面,所以平面; ……………………………4分
(Ⅱ)证明:因为平面,平面,
所以,又因为底面是矩形,
所以,,平面,平面.
所以,为的中点, ,
所以,,
所以平面, . ………………………………8分
(Ⅲ)………………12分.
22、解(1)因为,所以
因为所以,所以,………………4分
(2)因为,所以函数在区间上单调递减,因此函数在区间上的值域为,从而,即m,n为方程两个大于不等实根,,……………………………………………………8分
(3)因为,所以,因此
当时
当时或,
当时或,
因此满足的的集合为………………………………………………………12分
高一数学试卷
一、单选题
1、已知集合M={x|},N={y|,x∈R},则M∩N=( )
A.? B. {x|x≥1} C.{x|x>1} D.{x| x≥1或x<0}
2、下列函数中,既是偶函数又在区间(-∞,0)上单调递减的是( )
A. B. C. D.
3、若过两点的直线的倾斜角为,则( )
A. B. C.3 D.-3
4、设,是条不同的直线,是一个平面,以下命题正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
5、若点P(3,4)和点Q(a,b)关于直线对称,则( )
A., B.,
C., D.,
6、已知函数,则
A.1 B. C.2019 D.
7、已知函数,则不等式的解集为( )
A. B. C. D.
8、已知为定义在上的奇函数,,且对任意的时,当时,则不等式的解集为( )
A. B. C. D.
9、函数的图象大致为( )
A. B.
C. D.
10、已知是上的减函数,则a的取值范围是
A. B. C. D.
11、已知函数,则使得的x的范围是(????)
A. B. C. D.
12、已知图中的网格是由边长为的小正方形组成的,一个几何体的三视图如图中的粗实线所示,则这个几何体的体积为( )
A.8 B. C. D.
二、填空题
13、函数的零点是____________.
14、如图,平面,,,,,分别为的中点,则三棱锥的体积为________.
15、已知直线与直线互相垂直,则实数=________.
16、一个四棱锥的俯视图如图所示,它的外接球的球心到底面的距离是该球半径的一半,则这个四棱锥的侧视图的面积为______.
三、解答题
17、(10分)计算下列各式:
(1);
(2).
18、(12分)已知R为实数集,集合A={x|1
(2)若A∩C=C,求实数m的取值范围
19、(12分)已知直线 ,
(Ⅰ)若,求实数的值;
(Ⅱ)当时,求直线与之间的距离.
20、(12分)已知函数,.
(1)当时,求的值域;
(2)设的最小值为,请写出的表达式,并求的解.
21、(12分)如图,在四棱锥中,底面是矩形,平面,且,,点为线段的中点.
(Ⅰ)求证:平面;
(Ⅱ)求证:;
(Ⅲ)求三棱锥的体积.
22、(12分)已知函数其中
(1)解关于的不等式;
(2)若函数在区间上的值域为,求实数的取值范围;
(3)设函数,求满足的的集合。
广丰一中2018-2019学年度下学期期初考试高一数学参考答案
一、单选题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
D
D
A
D
D
C
B
D
A
B
二、填空题
13、1或-4 14、 15、0 16、
三、解答题
17.解(1)原式==-5.…………………….5分
(2)原式=……………………….10分
18、解(1)由得,所以…………3分
因为,,
所以. …………………6分
(2)因为,所以,分两种情况讨论,
当时,由,解得 …………………8分
当时,由此不等式组无解,……………10分
故实数的取值范围是………………………………………………12分
19、解(Ⅰ)由l1⊥l2可得:a+3(a﹣2)=0,
解得;……………………………………..6分
(Ⅱ)当l1∥l2时,有,
解得a=3,……………………………………..8分
此时,l1,l2的方程分别为:3x+3y+1=0,x+y=0即3x+3y=0,………………10分
故它们之间的距离为.……………………………………………..12分
20、 解(1)时,开口向上,对称轴为,
在上为减函数,在上为增函数,
的值域为. ……………4分
(2)时,即时,在上为增函数,
,…………………………………………6分
时,即时,在上为减函数,在上为增函数,
…………………………………………………………………8分
时,即时,在上为减函数,
……………………………………………………………………….10分
时,或
时,或
综上所述:t=-2或t=4………………………………………….………………..12分
21、解(Ⅰ)证明:连接,交于点,连接,
因为是矩形对角线交点,所以为中点,
又已知为线段的中点,所以,又平面
平面,所以平面; ……………………………4分
(Ⅱ)证明:因为平面,平面,
所以,又因为底面是矩形,
所以,,平面,平面.
所以,为的中点, ,
所以,,
所以平面, . ………………………………8分
(Ⅲ)………………12分.
22、解(1)因为,所以
因为所以,所以,………………4分
(2)因为,所以函数在区间上单调递减,因此函数在区间上的值域为,从而,即m,n为方程两个大于不等实根,,……………………………………………………8分
(3)因为,所以,因此
当时
当时或,
当时或,
因此满足的的集合为………………………………………………………12分
同课章节目录
