湘教版八年级下册 2.1.1 多边形的内角和 (共19张PPT)
文档属性
| 名称 | 湘教版八年级下册 2.1.1 多边形的内角和 (共19张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-22 00:00:00 | ||
图片预览



文档简介
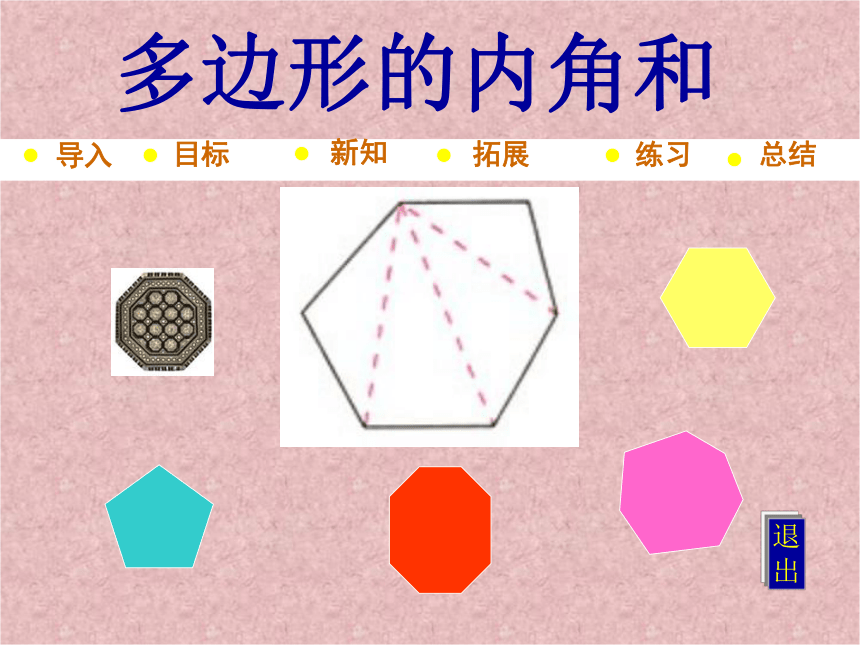
多边形的内角和
导入
目标
拓展
练习
退出
新知
总结
你能从下列图形中找出一些平面图形吗?
找一找
学习目标
1.使学生了解多边形的内角等概念。
2.能通过不同方法探索多边形的内角和公式,并会应用它们进行有关计算。
学习重难点
教学重点:多边形的内角和公式。
教学难点: 如何把多边形转化成三角形,用分割多边形法推导多边形的内角和。
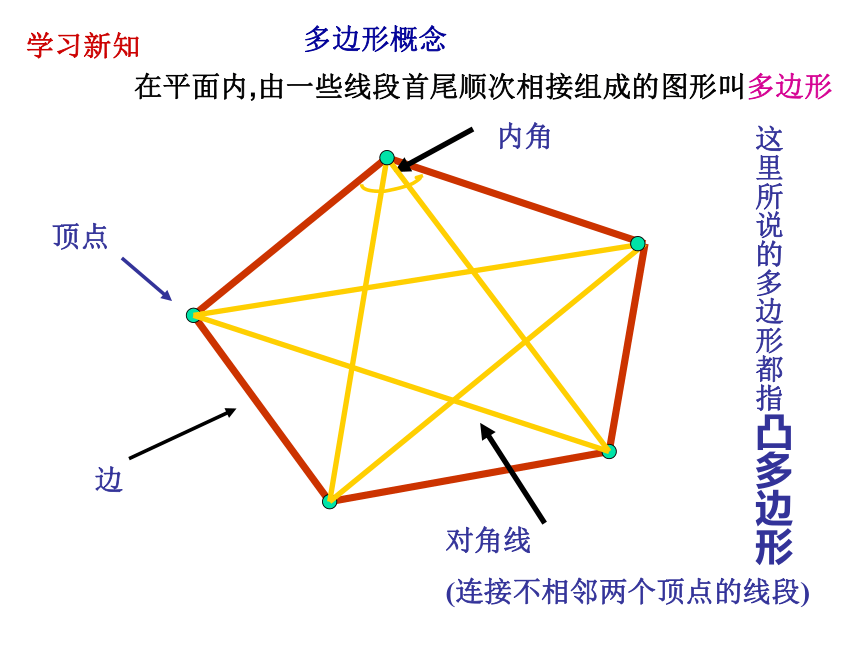
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
这里所说的多边形都指凸多边形
在平面内,由一些线段首尾顺次相接组成的图形叫多边形
多边形概念
学习新知
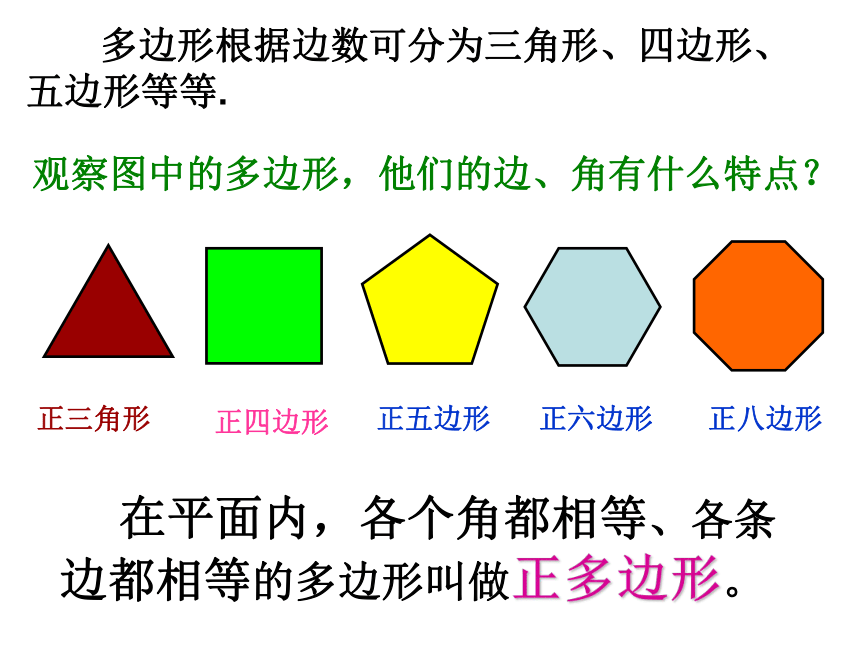
观察图中的多边形,他们的边、角有什么特点?
在平面内,各个角都相等、各条边都相等的多边形叫做正多边形。
正三角形
正四边形
正五边形
正六边形
正八边形
多边形根据边数可分为三角形、四边形、五边形等等.
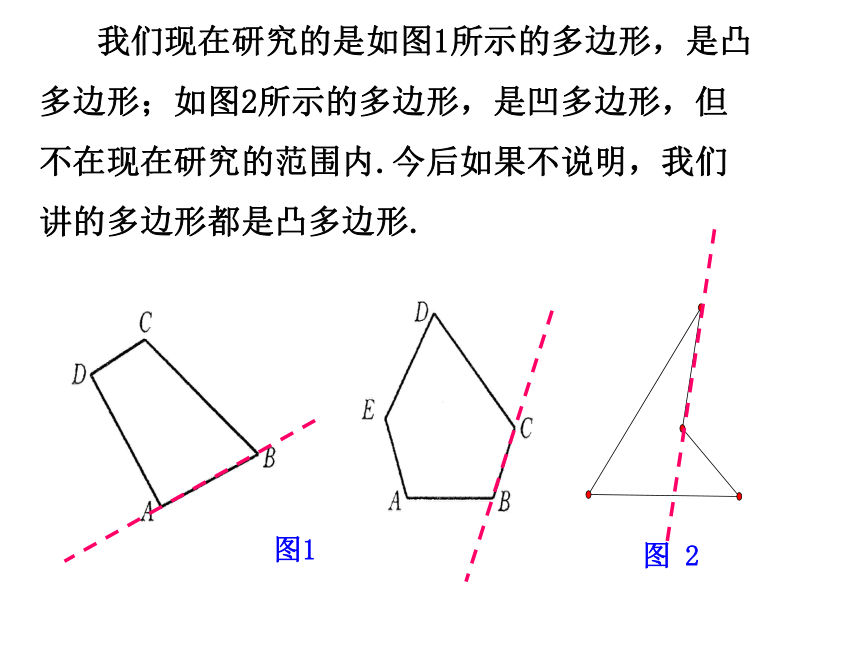
图 2
我们现在研究的是如图1所示的多边形,是凸多边形;如图2所示的多边形,是凹多边形,但不在现在研究的范围内.今后如果不说明,我们讲的多边形都是凸多边形.
我们怎样求多边形的内角和?
1、三角形的内角和是 _____ .
2、你能够利用三角形的内角和求四边形的内角和吗?试试看?
思路:多边形内角和问题转化为三角形 问题来解决.
四边形的内角和为3600
1800
做一做
n-2
3
2
1
0
4
3
2
1
n-3
1800
3600
5400
7200
(n-2) ×1800
从n边形的一个顶点可以引_____对角线,把多边形分成____个三角形.
n边形的内角和等于______
n-3
n-2
(n-2) ×1800
探究1
多边形边数 3 4 5 6 n
从一个顶点引对角线的条数
分成的三角形个数
多边形的内角和
…
…
…
…
…
…
3
4
5
6
7
n
1
n-2
2
3
4
5
180°
360°
540°
720°
900°
(n-2)
·180°
(n-2) ·180°
(7-2) ·180°
(6-2) ·180°
(5-2) ·180°
(4-2) ·180°
(3-2) ·180°
多边形 边数 图形 分成三角形的个数 内角和 计算规律
三角形
四边形
五边形
六边形
七边形
n边形
归纳、得出公式
综上所述,设多边形的边数为n,
则 n边形的内角和等于
说明:
多边形的内角和仅与边数有关,与多边形的大小、形状无关。
www.yousee123.com
E
A
B
C
D
.
O
180 × 5 – 360 = 540
探究
动脑筋:P35
1. 求十边形的内角和的度数.
解 :(10-2)×180°
=1440°.
例题讲解
跟踪练习:(1)求六边形的内角和的度数.
(2)求八边形的内角和的度数.
2. 如果一个多边形的内角和是1980度,求边数。
解:设边数为n,则
(n - 2)· 180 = 1980
解得: n = 13
∴这是一个十三边形。
例题讲解
跟踪练习: 如果一个多边形的内角和是2340度,求边数。
(n - 2) ? 180°
1260°
十一
108°
1、n边形的内角和等于__________,
九边形的内角和等于_________。
2、一个多边形的内角和等于1620°,
那么它是______边形.
3、正五边形的每一个内角的度数是_____。
4、多边形的内角和随着边数的增加而 ,
边数增加一条时,它的内角和增加 度 .
增 加
180
5、过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形。这个多边形是几边形?它的内角和是多少?
9000
七
2.若正n边形的一个内角是144度,则n=_______.
解:由多边形的内角和公式可得:
(n -2) · 180 = 144n
180n – 360 = 144n
180n -144n=360
36n = 360
n = 10
10
1.如果十二边形的每一个内角都相等,那么每个内角是______度。
150
【跟踪训练】
3.在四边形ABCD中,∠A=120度,∠B︰∠C︰∠D=3︰4︰5,求∠B,∠C,∠D的度数.
解:设∠B,∠C,∠D的度数分别是3x, 4x, 5x度,由四边形的内角和等于360度可得:
120 + 3x + 4x + 5x = 360
12x = 240
x = 20
所以 3x = 60
4x = 80
5x = 100
答:∠B,∠C,∠D的度数分别为60度,80度,100度.
试一试,练练你的“本领”
有一把锋利的“小刀”,把你 的课桌(四边形)一个角削去,剩下的课桌是一个几边形?
①
②
③
A
B
C
D
E
F
M
N
通过这节课的学习活动你有哪些收获?
你还有什么困惑吗?
导入
目标
拓展
练习
退出
新知
总结
你能从下列图形中找出一些平面图形吗?
找一找
学习目标
1.使学生了解多边形的内角等概念。
2.能通过不同方法探索多边形的内角和公式,并会应用它们进行有关计算。
学习重难点
教学重点:多边形的内角和公式。
教学难点: 如何把多边形转化成三角形,用分割多边形法推导多边形的内角和。
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
这里所说的多边形都指凸多边形
在平面内,由一些线段首尾顺次相接组成的图形叫多边形
多边形概念
学习新知
观察图中的多边形,他们的边、角有什么特点?
在平面内,各个角都相等、各条边都相等的多边形叫做正多边形。
正三角形
正四边形
正五边形
正六边形
正八边形
多边形根据边数可分为三角形、四边形、五边形等等.
图 2
我们现在研究的是如图1所示的多边形,是凸多边形;如图2所示的多边形,是凹多边形,但不在现在研究的范围内.今后如果不说明,我们讲的多边形都是凸多边形.
我们怎样求多边形的内角和?
1、三角形的内角和是 _____ .
2、你能够利用三角形的内角和求四边形的内角和吗?试试看?
思路:多边形内角和问题转化为三角形 问题来解决.
四边形的内角和为3600
1800
做一做
n-2
3
2
1
0
4
3
2
1
n-3
1800
3600
5400
7200
(n-2) ×1800
从n边形的一个顶点可以引_____对角线,把多边形分成____个三角形.
n边形的内角和等于______
n-3
n-2
(n-2) ×1800
探究1
多边形边数 3 4 5 6 n
从一个顶点引对角线的条数
分成的三角形个数
多边形的内角和
…
…
…
…
…
…
3
4
5
6
7
n
1
n-2
2
3
4
5
180°
360°
540°
720°
900°
(n-2)
·180°
(n-2) ·180°
(7-2) ·180°
(6-2) ·180°
(5-2) ·180°
(4-2) ·180°
(3-2) ·180°
多边形 边数 图形 分成三角形的个数 内角和 计算规律
三角形
四边形
五边形
六边形
七边形
n边形
归纳、得出公式
综上所述,设多边形的边数为n,
则 n边形的内角和等于
说明:
多边形的内角和仅与边数有关,与多边形的大小、形状无关。
www.yousee123.com
E
A
B
C
D
.
O
180 × 5 – 360 = 540
探究
动脑筋:P35
1. 求十边形的内角和的度数.
解 :(10-2)×180°
=1440°.
例题讲解
跟踪练习:(1)求六边形的内角和的度数.
(2)求八边形的内角和的度数.
2. 如果一个多边形的内角和是1980度,求边数。
解:设边数为n,则
(n - 2)· 180 = 1980
解得: n = 13
∴这是一个十三边形。
例题讲解
跟踪练习: 如果一个多边形的内角和是2340度,求边数。
(n - 2) ? 180°
1260°
十一
108°
1、n边形的内角和等于__________,
九边形的内角和等于_________。
2、一个多边形的内角和等于1620°,
那么它是______边形.
3、正五边形的每一个内角的度数是_____。
4、多边形的内角和随着边数的增加而 ,
边数增加一条时,它的内角和增加 度 .
增 加
180
5、过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形。这个多边形是几边形?它的内角和是多少?
9000
七
2.若正n边形的一个内角是144度,则n=_______.
解:由多边形的内角和公式可得:
(n -2) · 180 = 144n
180n – 360 = 144n
180n -144n=360
36n = 360
n = 10
10
1.如果十二边形的每一个内角都相等,那么每个内角是______度。
150
【跟踪训练】
3.在四边形ABCD中,∠A=120度,∠B︰∠C︰∠D=3︰4︰5,求∠B,∠C,∠D的度数.
解:设∠B,∠C,∠D的度数分别是3x, 4x, 5x度,由四边形的内角和等于360度可得:
120 + 3x + 4x + 5x = 360
12x = 240
x = 20
所以 3x = 60
4x = 80
5x = 100
答:∠B,∠C,∠D的度数分别为60度,80度,100度.
试一试,练练你的“本领”
有一把锋利的“小刀”,把你 的课桌(四边形)一个角削去,剩下的课桌是一个几边形?
①
②
③
A
B
C
D
E
F
M
N
通过这节课的学习活动你有哪些收获?
你还有什么困惑吗?
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
