高中物理人教版必修二 圆周运动 检测题 Word版含解析
文档属性
| 名称 | 高中物理人教版必修二 圆周运动 检测题 Word版含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 363.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-03-21 00:00:00 | ||
图片预览




文档简介
高中物理人教版必修二 圆周运动 检测题
/
图K11-1
1.[2018·天津一中摸底] 如图K11-1所示, O1为皮带传动的主动轮的轴心,轮半径为 r1 ;O2为从动轮的轴心,轮半径为r3;r2为固定在从动轮上的小轮半径.已知 r3=2r1,2r2=3r1.A、B和C分别是3个轮边缘上的点,则A、B、C三点的向心加速度之比是 ( )
A.4∶2∶1 B.8∶4∶3
C.2∶1∶1 D.6∶3∶2
/
图K11-2
2.(多选)[2018·太原二模] 如图K11-2所示,双手端着半球形的玻璃碗,碗内放有三个相同的小玻璃球.双手晃动玻璃碗,当碗静止后碗口在同一水平面内,三小球沿碗的内壁在不同的水平面内做匀速圆周运动.不考虑摩擦作用,下列说法中正确的是 ( )
A.三个小球受到的合力大小相等
B.距碗口最近的小球的线速度最大
C.距碗底最近的小球的向心加速度最小
D.处于中间位置的小球的周期最小
/
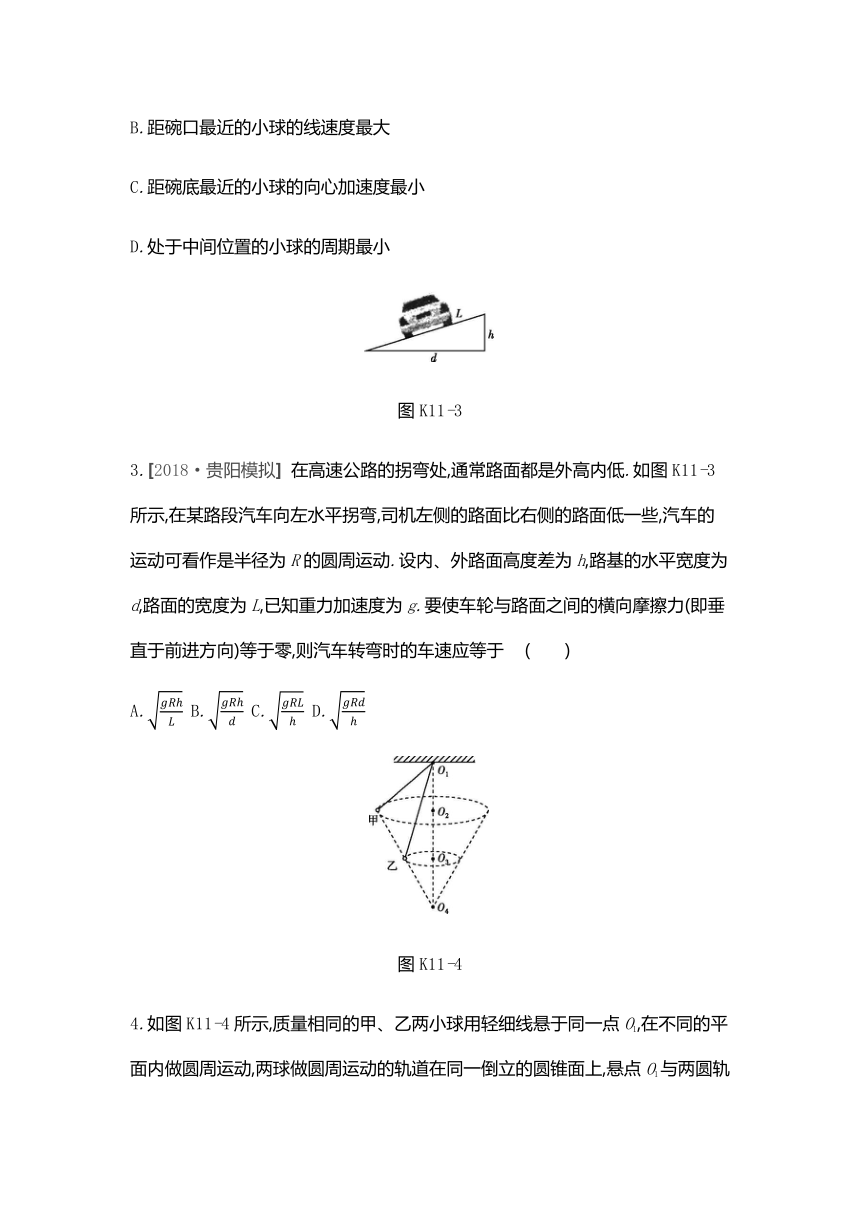
图K11-3
3.[2018·贵阳模拟] 在高速公路的拐弯处,通常路面都是外高内低.如图K11-3所示,在某路段汽车向左水平拐弯,司机左侧的路面比右侧的路面低一些,汽车的运动可看作是半径为R的圆周运动.设内、外路面高度差为h,路基的水平宽度为d,路面的宽度为L,已知重力加速度为g.要使车轮与路面之间的横向摩擦力(即垂直于前进方向)等于零,则汽车转弯时的车速应等于 ( )
A.
?????
??
B.
?????
??
C.
??????
?
D.
??????
?
/
图K11-4
4.如图K11-4所示,质量相同的甲、乙两小球用轻细线悬于同一点O1,在不同的平面内做圆周运动,两球做圆周运动的轨道在同一倒立的圆锥面上,悬点O1与两圆轨道的圆心O2、O3以及锥顶O4在同一竖直线上,且O2、O3将O1O4三等分,则甲、乙两球运动的角速度的比值为 ( )
A.1 B.
2
2
C.2 D.
2
/
图K11-5
5.如图K11-5所示,半径为R、内壁光滑的硬质小圆桶固定在小车上,小车以速度v在光滑的水平公路上做匀速运动,有一质量为m、可视为质点的光滑小铅球在小圆桶底端与小车保持相对静止,重力加速度为g.当小车与固定在地面上的障碍物相碰后,小车的速度立即变为零.关于碰后的运动(小车始终没有离开地面),下列说法正确的是 ( )
A.铅球能上升的最大高度一定等于
??
2
2??
B.无论v有多大,铅球上升的最大高度不超过
??
2
2??
C.要使铅球一直不脱离圆桶,v的最小速度为
5????
D.若铅球能到达圆桶最高点,则铅球在最高点的速度大小可以等于零
/
图K11-6
6.[2018·宜昌一模] 如图K11-6所示,一块足够大的光滑平板能绕水平固定轴MN调节其与水平面所成的夹角,板上有一根长为l=0.60 m的轻细绳,它的一端系住一质量为m的小球P,另一端固定在板上的O点.当平板的倾角调为α时,先将轻绳平行于水平轴MN拉直,然后给小球一沿着平板并与轻绳垂直的初速度v0=3.0 m/s.若小球能保持在板面内做圆周运动,则倾角α的最大值为(重力加速度g取10 m/s2) ( )
A.30° B.45° C.60° D.90°
/技能提升
/
图K11-7
7.(多选)[2019·辽宁六校联考] 如图K11-7所示,转动轴垂直于光滑水平面,交点O的上方h高处固定着细绳,细绳的下端拴接一质量为m的小球B,绳长l>h,转动轴带动小球在光滑水平面上做圆周运动,重力加速度为g.当转动的角速度ω逐渐增大时,下列说法正确的是 ( )
A.小球始终受到三个力的作用
B.细绳上的拉力始终不变
C.要使小球不离开水平面,角速度的最大值为
??
?
D.若l<
2
h,则当小球的角速度为
2
??
??
时,细绳与转动轴的夹角为45°
/
图K11-8
8.(多选)一同学玩飞镖游戏,如图K11-8所示,已知飞镖距圆盘为L,且对准圆盘上边缘的A点水平飞出,初速度为v0,飞镖抛出的同时,圆盘绕垂直于圆盘且过盘心O点的水平轴匀速转动.若飞镖恰好击中A点,重力加速度为g,则下列说法正确的是 ( )
A.从飞镖抛出到恰好击中A点,圆盘一定转动半周
B.从飞镖抛出到恰好击中A点的时间为
??
??
0
C.圆盘的半径为
??
??
2
4
??
0
2
D.圆盘转动的角速度为
2??π
??
0
??
(k=1,2,3,…)
9.如图K11-9所示,两个四分之三竖直圆弧轨道固定在同一水平地面上,半径R相同,左侧轨道由金属凹槽制成,右侧轨道由金属圆管制成,均可视为光滑轨道.在两轨道右侧的正上方分别将金属小球A和B由静止释放,小球距离地面的高度分别为hA、hB,下列说法正确的是(重力加速度为g) ( )
/
图K11-9
A.若两小球均沿轨道运动并且均恰好到达轨道最高点,则两球释放的高度hAB.在A球能运动到轨道最高点的情况下,在轨道最低点时A球所受支持力的最小值为6mg
C.在B球能运动到轨道最高点的情况下,在轨道最低点时B球所受支持力的最小值为6mg
D.适当调整hA、hB,可使两球从轨道最高点飞出后均能恰好落在各自轨道右端开口处
/
图K11-10
10.(多选)如图K11-10所示,一个质量为m的光滑小环套在一根轻质细绳上,细绳的两端分别系在竖直的杆上A、B两点,让竖直杆以角速度ω匀速转动,此时小环在绳上C点,AC和BC与竖直方向的夹角分别为37°和53°,sin 37°=0.6,cos 37°=0.8,重力加速度为g,则 ( )
A.绳上的张力大小为
5
7
mg
B.绳子的长度为
35??
12
??
2
C.杆上A、B两点间的距离为
35??
12
??
2
D.环做圆周运动的向心加速度大小等于g
11.某同学设计了一个粗测玩具小车经过凹形桥模拟器最低点时的速度的实验.所用器材有:玩具小车(可视为质点)、压力式托盘秤、凹形桥模拟器(圆弧部分的半径为R=0.20 m).将凹形桥模拟器静置于托盘秤上,如图K11-11所示,托盘秤的示数为1.00 kg;将玩具小车静置于凹形桥模拟器最低点时,托盘秤的示数为1.40 kg;将小车从凹形桥模拟器某一位置释放,小车经过最低点后滑向另一侧,此过程中托盘秤的最大示数为1.80 kg,凹形桥模拟器与托盘间始终无相对滑动.重力加速度g取10 m/s2,求:
(1)玩具小车的质量m;
(2)玩具小车经过最低点时对凹形桥模拟器的压力大小F;
(3)玩具小车经过最低点时的速度大小v.
/
图K11-11
/挑战自我
12.现有一根长度L=1 m的刚性轻绳,其一端固定于O点,另一端系着质量m=0.5 kg的小球(可视为质点),将小球提至O点正上方的A点处,此时绳刚好伸直且无张力,如图K11-12所示.不计空气阻力,g取10 m/s2.
(1)为保证小球能在竖直面内做完整的圆周运动,在A点至少应给小球多大的水平速度?
(2)在A点将小球以速度v1=4 m/s水平抛出的瞬间,绳中的张力为多少?
(3)在A点将小球以速度v2=1 m/s水平抛出的瞬间,绳中是否有张力?若有张力,求其大小;若无张力,试求绳子再次伸直时所经历的时间.
/
图K11-12
课时作业(十一)
1.B [解析] A和B由同一皮带传动,线速度大小相等,由an=
??
2
??
可得,A、B两点的向心加速度之比
??
??
??
??
=
??
3
??
1
=2;C和B同转轴,角速度相等,由an=ω2r可得,B、C两点的向心加速度之比
??
??
??
??
=
??
3
??
2
=
4
3
,故aA∶aB∶aC=8∶4∶3,选项B 正确.
2.BC [解析] 设小球所在位置和碗对应的球心连线与水平方向的夹角为θ,由向心力公式得mgtan θ=man=m
??
2
??sin??
=m
2π
??
2
rsin θ,离碗口越近,夹角θ越大,加速度an越大,周期T越小,线速度v越大,选项B、C正确.
3.B [解析] 设路面倾角为θ,由牛顿第二定律得mgtan θ=m
??
2
??
,而tan θ=
?
??
,联立可得速度v=
?????
??
,选项B正确.
4.D [解析] 设连接甲球的细线与竖直方向的夹角为α,连接乙球的细线与竖直方向的夹角为β,O1、O2的距离为h,对甲和乙,分别有mgtan α=m
??
1
2
htan α,mgtan β=2m
??
2
2
htan β,联立可得
??
1
??
2
=
2
,选项D 正确.
5.B [解析] 若铅球能上升的最大高度不超过圆桶的半径,则铅球到最高点时速度为0,有mgh=
1
2
mv2,可得上升的最大高度h=
??
2
2??
,因上升的最大高度不超过圆桶的半径R,故速度v≤
2????
,此时铅球不脱离圆桶,选项C 错误;若铅球能到达圆桶最高点,则mg≤m
??
m
2
??
,则铅球在最高点的速度vm≥
????
,由
1
2
mv2=mg+
1
2
m
??
m
2
可得h<
??
2
2??
,选项B正确,选项A、D 错误.
6.A [解析] 小球恰好到达最高点时,由重力的分力mgsin α提供向心力,有mgsin α=m
??
m
2
??
,研究小球从被释放至到达最高点的过程,根据动能定理得-mglsin α=
1
2
m
??
m
2
-
1
2
m
??
0
2
,联立解得sin α=
1
2
,则α=30°,故α的最大值为30°,选项A正确.
7.CD [解析] 设小球与水平面接触,且水平面的弹力为0 时其角速度为ω0,由向心力公式得mgtan θ=m
??
0
2
lsin θ,小球不离开水平面的最大角速度ω0=
??
??cos??
=
??
?
,当角速度ω<
??
?
时,小球受重力、绳子拉力和水平面的弹力三个力,绳子拉力T=mω2lsin θ随角速度ω增大而增大;当ω>
??
?
时,小球与水平面分离,小球只受重力和绳子拉力两个力,绳子拉力T=
????
cos??
随夹角θ的变化而变化;若l<
2
h,则
2
??
??
>
??
?
,当角速度为
2
??
??
时,有mgtan θ=mω2lsin θ=
2
mgsin θ,细绳与转动轴的夹角θ=45°,选项C、D正确.
8.BC [解析] 飞镖要击中A点,圆盘将转动半周的奇数倍,选项A错误;飞镖在水平方向上做匀速直线运动,有L=v0t,击中A 的时间t=
??
??
0
,选项B正确;飞镖在竖直方向上做自由落体运动,有2R=
1
2
gt2,联立解得R=
??
??
2
4
??
0
2
,选项C正确;又t=
1
2
+??
2π
??
,故角速度ω=
1
2
+??
2π
??
0
??
(k=0,1,2,…),选项D 错误.
9.B [解析] 若小球A恰好能到左侧轨道的最高点,由mg=m
??
??
2
??
得vA=
????
,根据机械能守恒定律得mg(hA-2R)=
1
2
m
??
??
2
,解得hA=
5
2
R,若小球B恰好能到右侧轨道的最高点,在最高点的速度vB=0,根据机械能守恒定律得hB=2R,故hA>hB,A错误;设A球运动到轨道最低点时的速度为v1,有mghA=
1
2
m
??
1
2
,由牛顿第二定律得FNA-mg=m
??
1
2
??
,联立得A球在轨道最低点所受支持力的最小值FNA=6mg,设B球运动到轨道最低点时的速度为v2,有mghB=
1
2
m
??
2
2
,根据牛顿第二定律得FNB-mg=m
??
2
2
??
,联立得B球在轨道最低点所受支持力的最小值FNB=5mg,故B正确,C错误;小球A从最高点飞出后做平抛运动,下落高度为R时,水平位移的最小值xA=vA
2??
??
=
????
·
2??
??
=
2
R>R,所以A球落在轨道右端开口外侧,而适当调整hB,可使B球恰好落在轨道右端开口处,D错误.
10.ABD [解析] 对小环,有T(cos 37°+cos 53°)=mg,解得绳上的张力T=
5
7
mg,又有T(sin 37°+sin 53°)=mω2r,解得转动半径r=
??
??
2
,向心加速度an=g,绳长l=r
1
sin37°
+
1
sin 53°
=
35??
12
??
2
,选项A、B、D正确;杆上A、B两点间的距离为r
tan 53°?tan37°
=
7??
12
??
2
,选项C错误.
11.(1)0.40 kg (2)8.0 N (3)
2
m/s
[解析] (1)小车的质量m=1.40 kg-1.00 kg =0.40 kg
(2)凹形桥模拟器的质量m0=1.00 kg
设秤盘对凹形桥模拟器的支持力为FN,凹形桥模拟器对秤盘的压力为FN',根据力的平衡条件,对凹形桥模拟器,有F+m0g=FN
根据牛顿第三定律可得FN=FN'
而FN'=m示g
其中m示=1.80 kg
联立解得F=8.0 N
(3)小车通过最低点时,凹形桥模拟器对小车的支持力F'与小车重力的合力提供向心力,有
F'-mg=m
??
2
??
根据牛顿第三定律可得F'=F
联立解得v=
2
m/s
12.(1)
10
m/s (2)3 N (3)无张力 0.6 s
[解析] (1)小球做圆周运动的临界条件为在最高点时重力刚好提供其做圆周运动的向心力,即mg=m
??
0
2
??
解得v0=
????
=
10
m/s
(2)因为v1>v0,故绳中有张力,根据牛顿第二定律得
T+mg=m
??
1
2
??
解得T=3 N
(3)因为v2L2=(y-L)2+x2
x=v2t
y=
1
2
gt2
联立解得t=0.6 s(t=0舍去).
/
/
图K11-1
1.[2018·天津一中摸底] 如图K11-1所示, O1为皮带传动的主动轮的轴心,轮半径为 r1 ;O2为从动轮的轴心,轮半径为r3;r2为固定在从动轮上的小轮半径.已知 r3=2r1,2r2=3r1.A、B和C分别是3个轮边缘上的点,则A、B、C三点的向心加速度之比是 ( )
A.4∶2∶1 B.8∶4∶3
C.2∶1∶1 D.6∶3∶2
/
图K11-2
2.(多选)[2018·太原二模] 如图K11-2所示,双手端着半球形的玻璃碗,碗内放有三个相同的小玻璃球.双手晃动玻璃碗,当碗静止后碗口在同一水平面内,三小球沿碗的内壁在不同的水平面内做匀速圆周运动.不考虑摩擦作用,下列说法中正确的是 ( )
A.三个小球受到的合力大小相等
B.距碗口最近的小球的线速度最大
C.距碗底最近的小球的向心加速度最小
D.处于中间位置的小球的周期最小
/
图K11-3
3.[2018·贵阳模拟] 在高速公路的拐弯处,通常路面都是外高内低.如图K11-3所示,在某路段汽车向左水平拐弯,司机左侧的路面比右侧的路面低一些,汽车的运动可看作是半径为R的圆周运动.设内、外路面高度差为h,路基的水平宽度为d,路面的宽度为L,已知重力加速度为g.要使车轮与路面之间的横向摩擦力(即垂直于前进方向)等于零,则汽车转弯时的车速应等于 ( )
A.
?????
??
B.
?????
??
C.
??????
?
D.
??????
?
/
图K11-4
4.如图K11-4所示,质量相同的甲、乙两小球用轻细线悬于同一点O1,在不同的平面内做圆周运动,两球做圆周运动的轨道在同一倒立的圆锥面上,悬点O1与两圆轨道的圆心O2、O3以及锥顶O4在同一竖直线上,且O2、O3将O1O4三等分,则甲、乙两球运动的角速度的比值为 ( )
A.1 B.
2
2
C.2 D.
2
/
图K11-5
5.如图K11-5所示,半径为R、内壁光滑的硬质小圆桶固定在小车上,小车以速度v在光滑的水平公路上做匀速运动,有一质量为m、可视为质点的光滑小铅球在小圆桶底端与小车保持相对静止,重力加速度为g.当小车与固定在地面上的障碍物相碰后,小车的速度立即变为零.关于碰后的运动(小车始终没有离开地面),下列说法正确的是 ( )
A.铅球能上升的最大高度一定等于
??
2
2??
B.无论v有多大,铅球上升的最大高度不超过
??
2
2??
C.要使铅球一直不脱离圆桶,v的最小速度为
5????
D.若铅球能到达圆桶最高点,则铅球在最高点的速度大小可以等于零
/
图K11-6
6.[2018·宜昌一模] 如图K11-6所示,一块足够大的光滑平板能绕水平固定轴MN调节其与水平面所成的夹角,板上有一根长为l=0.60 m的轻细绳,它的一端系住一质量为m的小球P,另一端固定在板上的O点.当平板的倾角调为α时,先将轻绳平行于水平轴MN拉直,然后给小球一沿着平板并与轻绳垂直的初速度v0=3.0 m/s.若小球能保持在板面内做圆周运动,则倾角α的最大值为(重力加速度g取10 m/s2) ( )
A.30° B.45° C.60° D.90°
/技能提升
/
图K11-7
7.(多选)[2019·辽宁六校联考] 如图K11-7所示,转动轴垂直于光滑水平面,交点O的上方h高处固定着细绳,细绳的下端拴接一质量为m的小球B,绳长l>h,转动轴带动小球在光滑水平面上做圆周运动,重力加速度为g.当转动的角速度ω逐渐增大时,下列说法正确的是 ( )
A.小球始终受到三个力的作用
B.细绳上的拉力始终不变
C.要使小球不离开水平面,角速度的最大值为
??
?
D.若l<
2
h,则当小球的角速度为
2
??
??
时,细绳与转动轴的夹角为45°
/
图K11-8
8.(多选)一同学玩飞镖游戏,如图K11-8所示,已知飞镖距圆盘为L,且对准圆盘上边缘的A点水平飞出,初速度为v0,飞镖抛出的同时,圆盘绕垂直于圆盘且过盘心O点的水平轴匀速转动.若飞镖恰好击中A点,重力加速度为g,则下列说法正确的是 ( )
A.从飞镖抛出到恰好击中A点,圆盘一定转动半周
B.从飞镖抛出到恰好击中A点的时间为
??
??
0
C.圆盘的半径为
??
??
2
4
??
0
2
D.圆盘转动的角速度为
2??π
??
0
??
(k=1,2,3,…)
9.如图K11-9所示,两个四分之三竖直圆弧轨道固定在同一水平地面上,半径R相同,左侧轨道由金属凹槽制成,右侧轨道由金属圆管制成,均可视为光滑轨道.在两轨道右侧的正上方分别将金属小球A和B由静止释放,小球距离地面的高度分别为hA、hB,下列说法正确的是(重力加速度为g) ( )
/
图K11-9
A.若两小球均沿轨道运动并且均恰好到达轨道最高点,则两球释放的高度hA
C.在B球能运动到轨道最高点的情况下,在轨道最低点时B球所受支持力的最小值为6mg
D.适当调整hA、hB,可使两球从轨道最高点飞出后均能恰好落在各自轨道右端开口处
/
图K11-10
10.(多选)如图K11-10所示,一个质量为m的光滑小环套在一根轻质细绳上,细绳的两端分别系在竖直的杆上A、B两点,让竖直杆以角速度ω匀速转动,此时小环在绳上C点,AC和BC与竖直方向的夹角分别为37°和53°,sin 37°=0.6,cos 37°=0.8,重力加速度为g,则 ( )
A.绳上的张力大小为
5
7
mg
B.绳子的长度为
35??
12
??
2
C.杆上A、B两点间的距离为
35??
12
??
2
D.环做圆周运动的向心加速度大小等于g
11.某同学设计了一个粗测玩具小车经过凹形桥模拟器最低点时的速度的实验.所用器材有:玩具小车(可视为质点)、压力式托盘秤、凹形桥模拟器(圆弧部分的半径为R=0.20 m).将凹形桥模拟器静置于托盘秤上,如图K11-11所示,托盘秤的示数为1.00 kg;将玩具小车静置于凹形桥模拟器最低点时,托盘秤的示数为1.40 kg;将小车从凹形桥模拟器某一位置释放,小车经过最低点后滑向另一侧,此过程中托盘秤的最大示数为1.80 kg,凹形桥模拟器与托盘间始终无相对滑动.重力加速度g取10 m/s2,求:
(1)玩具小车的质量m;
(2)玩具小车经过最低点时对凹形桥模拟器的压力大小F;
(3)玩具小车经过最低点时的速度大小v.
/
图K11-11
/挑战自我
12.现有一根长度L=1 m的刚性轻绳,其一端固定于O点,另一端系着质量m=0.5 kg的小球(可视为质点),将小球提至O点正上方的A点处,此时绳刚好伸直且无张力,如图K11-12所示.不计空气阻力,g取10 m/s2.
(1)为保证小球能在竖直面内做完整的圆周运动,在A点至少应给小球多大的水平速度?
(2)在A点将小球以速度v1=4 m/s水平抛出的瞬间,绳中的张力为多少?
(3)在A点将小球以速度v2=1 m/s水平抛出的瞬间,绳中是否有张力?若有张力,求其大小;若无张力,试求绳子再次伸直时所经历的时间.
/
图K11-12
课时作业(十一)
1.B [解析] A和B由同一皮带传动,线速度大小相等,由an=
??
2
??
可得,A、B两点的向心加速度之比
??
??
??
??
=
??
3
??
1
=2;C和B同转轴,角速度相等,由an=ω2r可得,B、C两点的向心加速度之比
??
??
??
??
=
??
3
??
2
=
4
3
,故aA∶aB∶aC=8∶4∶3,选项B 正确.
2.BC [解析] 设小球所在位置和碗对应的球心连线与水平方向的夹角为θ,由向心力公式得mgtan θ=man=m
??
2
??sin??
=m
2π
??
2
rsin θ,离碗口越近,夹角θ越大,加速度an越大,周期T越小,线速度v越大,选项B、C正确.
3.B [解析] 设路面倾角为θ,由牛顿第二定律得mgtan θ=m
??
2
??
,而tan θ=
?
??
,联立可得速度v=
?????
??
,选项B正确.
4.D [解析] 设连接甲球的细线与竖直方向的夹角为α,连接乙球的细线与竖直方向的夹角为β,O1、O2的距离为h,对甲和乙,分别有mgtan α=m
??
1
2
htan α,mgtan β=2m
??
2
2
htan β,联立可得
??
1
??
2
=
2
,选项D 正确.
5.B [解析] 若铅球能上升的最大高度不超过圆桶的半径,则铅球到最高点时速度为0,有mgh=
1
2
mv2,可得上升的最大高度h=
??
2
2??
,因上升的最大高度不超过圆桶的半径R,故速度v≤
2????
,此时铅球不脱离圆桶,选项C 错误;若铅球能到达圆桶最高点,则mg≤m
??
m
2
??
,则铅球在最高点的速度vm≥
????
,由
1
2
mv2=mg+
1
2
m
??
m
2
可得h<
??
2
2??
,选项B正确,选项A、D 错误.
6.A [解析] 小球恰好到达最高点时,由重力的分力mgsin α提供向心力,有mgsin α=m
??
m
2
??
,研究小球从被释放至到达最高点的过程,根据动能定理得-mglsin α=
1
2
m
??
m
2
-
1
2
m
??
0
2
,联立解得sin α=
1
2
,则α=30°,故α的最大值为30°,选项A正确.
7.CD [解析] 设小球与水平面接触,且水平面的弹力为0 时其角速度为ω0,由向心力公式得mgtan θ=m
??
0
2
lsin θ,小球不离开水平面的最大角速度ω0=
??
??cos??
=
??
?
,当角速度ω<
??
?
时,小球受重力、绳子拉力和水平面的弹力三个力,绳子拉力T=mω2lsin θ随角速度ω增大而增大;当ω>
??
?
时,小球与水平面分离,小球只受重力和绳子拉力两个力,绳子拉力T=
????
cos??
随夹角θ的变化而变化;若l<
2
h,则
2
??
??
>
??
?
,当角速度为
2
??
??
时,有mgtan θ=mω2lsin θ=
2
mgsin θ,细绳与转动轴的夹角θ=45°,选项C、D正确.
8.BC [解析] 飞镖要击中A点,圆盘将转动半周的奇数倍,选项A错误;飞镖在水平方向上做匀速直线运动,有L=v0t,击中A 的时间t=
??
??
0
,选项B正确;飞镖在竖直方向上做自由落体运动,有2R=
1
2
gt2,联立解得R=
??
??
2
4
??
0
2
,选项C正确;又t=
1
2
+??
2π
??
,故角速度ω=
1
2
+??
2π
??
0
??
(k=0,1,2,…),选项D 错误.
9.B [解析] 若小球A恰好能到左侧轨道的最高点,由mg=m
??
??
2
??
得vA=
????
,根据机械能守恒定律得mg(hA-2R)=
1
2
m
??
??
2
,解得hA=
5
2
R,若小球B恰好能到右侧轨道的最高点,在最高点的速度vB=0,根据机械能守恒定律得hB=2R,故hA>hB,A错误;设A球运动到轨道最低点时的速度为v1,有mghA=
1
2
m
??
1
2
,由牛顿第二定律得FNA-mg=m
??
1
2
??
,联立得A球在轨道最低点所受支持力的最小值FNA=6mg,设B球运动到轨道最低点时的速度为v2,有mghB=
1
2
m
??
2
2
,根据牛顿第二定律得FNB-mg=m
??
2
2
??
,联立得B球在轨道最低点所受支持力的最小值FNB=5mg,故B正确,C错误;小球A从最高点飞出后做平抛运动,下落高度为R时,水平位移的最小值xA=vA
2??
??
=
????
·
2??
??
=
2
R>R,所以A球落在轨道右端开口外侧,而适当调整hB,可使B球恰好落在轨道右端开口处,D错误.
10.ABD [解析] 对小环,有T(cos 37°+cos 53°)=mg,解得绳上的张力T=
5
7
mg,又有T(sin 37°+sin 53°)=mω2r,解得转动半径r=
??
??
2
,向心加速度an=g,绳长l=r
1
sin37°
+
1
sin 53°
=
35??
12
??
2
,选项A、B、D正确;杆上A、B两点间的距离为r
tan 53°?tan37°
=
7??
12
??
2
,选项C错误.
11.(1)0.40 kg (2)8.0 N (3)
2
m/s
[解析] (1)小车的质量m=1.40 kg-1.00 kg =0.40 kg
(2)凹形桥模拟器的质量m0=1.00 kg
设秤盘对凹形桥模拟器的支持力为FN,凹形桥模拟器对秤盘的压力为FN',根据力的平衡条件,对凹形桥模拟器,有F+m0g=FN
根据牛顿第三定律可得FN=FN'
而FN'=m示g
其中m示=1.80 kg
联立解得F=8.0 N
(3)小车通过最低点时,凹形桥模拟器对小车的支持力F'与小车重力的合力提供向心力,有
F'-mg=m
??
2
??
根据牛顿第三定律可得F'=F
联立解得v=
2
m/s
12.(1)
10
m/s (2)3 N (3)无张力 0.6 s
[解析] (1)小球做圆周运动的临界条件为在最高点时重力刚好提供其做圆周运动的向心力,即mg=m
??
0
2
??
解得v0=
????
=
10
m/s
(2)因为v1>v0,故绳中有张力,根据牛顿第二定律得
T+mg=m
??
1
2
??
解得T=3 N
(3)因为v2
x=v2t
y=
1
2
gt2
联立解得t=0.6 s(t=0舍去).
/
