第二章《相交线与平行线》单元检测A(含解析)
文档属性
| 名称 | 第二章《相交线与平行线》单元检测A(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 314.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-22 11:01:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二章《相交线与平行线》单元检测A
评卷人 得 分
一.选择题(共12小题,满分36分,每小题3分)
1.如图所示,点P到直线l的距离是( )
A.线段PA的长度 B.线段PB的长度
C.线段PC的长度 D.线段PD的长度
2.如图,直线AB、CD相交于点O,EO⊥CD.下列说法错误的是( )
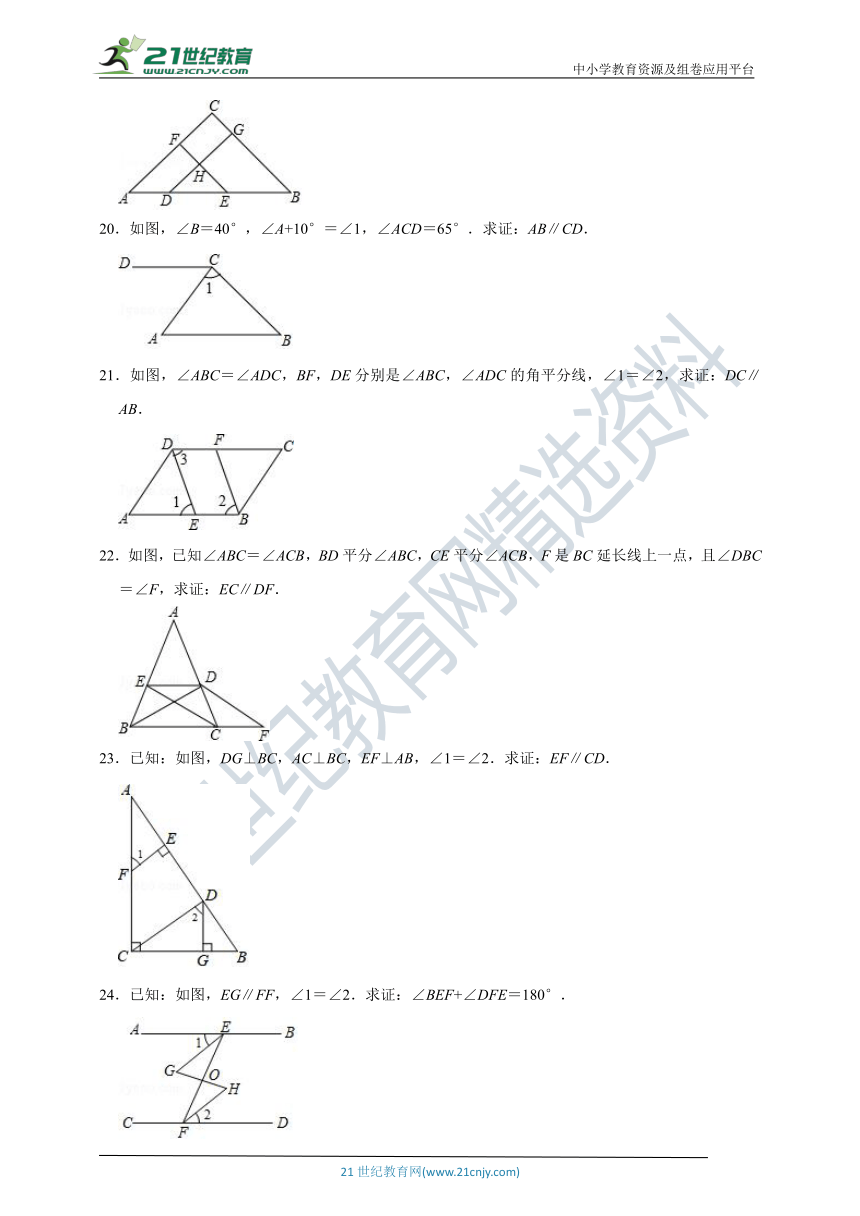
A.∠AOD=∠BOC B.∠AOE+∠BOD=90°
C.∠AOC=∠AOE D.∠AOD+∠BOD=180°
3.如图,下列各组角中,互为对顶角的是( )
A.∠1和∠2 B.∠1和∠3 C.∠2和∠4 D.∠2和∠5
4.下列画图的语句中,正确的为( )
A.画直线AB=10cm
B.画射线OB=10cm
C.延长射线BA到C,使BA=BC
D.画线段CD=2cm
5.如图所示,直线AB,CD相交于点O,已知∠AOD=160°,则∠BOC的大小为( )
A.20° B.60° C.70° D.160°
6.如图,直线a,b被直线c所截,下列条件中,不能判定a∥b( )
A.∠2=∠4 B.∠1+∠4=180° C.∠5=∠4 D.∠1=∠3
7.如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是( )
A.∠4,∠2 B.∠2,∠6 C.∠5,∠4 D.∠2,∠4
8.如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
A.112° B.110° C.108° D.106°
9.如图,AB∥CD,直线EF分别与AB、CD交于点E、F,若∠AEF=40°,则∠EFD的度数为( )
A.20° B.40° C.50° D.140°
10.如图,AB∥CD,∠1=30°,则∠2的度数是( )
A.120° B.130° C.150° D.135°
11.如图,AF是∠BAC的平分线,DF∥AC,若∠1=35°,则∠BAF的度数为( )
A.17.5° B.35° C.55° D.70°
12.如图,已知DE∥BC,如果∠1=70°,那么∠B的度数为( )
A.70° B.100° C.110° D.120°
评卷人 得 分
二.填空题(共6小题,满分24分,每小题4分)
13.如图,直线AB,CD相交于点O,EO⊥AB于点O,∠EOD=50°,则∠BOC的度数为 .
14.已知:如图直线AB与CD相交于点O,OE⊥AB,∠COE=60°,则∠BOD等于 度.
15.如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为 .(任意添加一个符合题意的条件即可)
16.两个角的两边分别平行,其中一个角比另一个角的4倍少30°,这两个角是 .
17.如图,AB∥CD,若∠E=34°,∠D=20°,则∠B的度数为 .
18.将一张矩形纸条与一块三角板如图放置,若∠1=36°,则∠2= .
评卷人 得 分
三.解答题(共8小题,满分60分)
19.如图,在△ABC中,∠A=∠B,D、E是边AB上的点,DG∥AC,EF∥BC,DG、EF相交于点H.
(1)∠HDE与∠HED是否相等?并说明理由.
解:∠HDE=∠HED.理由如下:
∵DG∥AC (已知)
∴ = ( )
∵EF∥BC(已知)
∴ = ( )
又∵∠A=∠B(已知)
∴ = ( ).
(2)如果∠C=90°,DG、EF有何位置关系?并仿照 (1)中的解答方法说明理由.
解: .理由如下:
20.如图,∠B=40°,∠A+10°=∠1,∠ACD=65°.求证:AB∥CD.
21.如图,∠ABC=∠ADC,BF,DE分别是∠ABC,∠ADC的角平分线,∠1=∠2,求证:DC∥AB.
22.如图,已知∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,F是BC延长线上一点,且∠DBC=∠F,求证:EC∥DF.
23.已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.求证:EF∥CD.
24.已知:如图,EG∥FF,∠1=∠2.求证:∠BEF+∠DFE=180°.
25.如图,AB∥EF,AD平分∠BAC,且∠C=45°,∠CDE=125°,求∠ADF的度数.
26.如图1,点E在直线AB上,点F在直线CD上,EG⊥FG.
(1)若∠BEG+∠DFG=90°,请判断AB与CD的位置关系,并说明理由;
(2)如图2,在(1)的结论下,当EG⊥FG保持不变,EG上有一点M,使∠MFG=2∠DFG,则∠BEG与∠MFD存在怎样的数量关系?并说明理由.
(3)如图2,若移动点M,使∠MFG=n∠DFG,请直接写出∠BEG与∠MFD的数量关系.
答案与解析
一.选择题(共12小题,满分36分,每小题3分)
1.【分析】根据点到直线的距离是垂线段的长度,可得答案.
【解答】解:由题意,得
点P到直线l的距离是线段PB的长度,
故选:B.
2.【分析】根据对顶角性质、邻补角定义及垂线的定义逐一判断可得.
【解答】解:A、∠AOD与∠BOC是对顶角,所以∠AOD=∠BOC,此选项正确;
B、由EO⊥CD知∠DOE=90°,所以∠AOE+∠BOD=90°,此选项正确;
C、∠AOC与∠BOD是对顶角,所以∠AOC=∠BOD,此选项错误;
D、∠AOD与∠BOD是邻补角,所以∠AOD+∠BOD=180°,此选项正确;
故选:C.
3.【分析】直接利用对顶角的定义得出答案.
【解答】解:互为对顶角的是:∠1和∠2.
故选:A.
4.【分析】根据直线、射线、线段的性质即可一一判断.
【解答】解:A、错误.直线没有长度;
B、错误.射线没有长度;
C、错误.射线有无限延伸性,不需要延长;
D、正确.
故选:D.
5.【分析】根据对顶角相等解答即可.
【解答】解:∵∠AOD=160°,
∴∠BOC=∠AOD=160°,
故选:D.
6.【分析】根据同位角相等,两直线平行;同旁内角互补,两直线平行;内错角相等,两直线平行,进行判断即可.
【解答】解:由∠2=∠4或∠1+∠4=180°或∠5=∠4,可得a∥b;
由∠1=∠3,不能得到a∥b;
故选:D.
7.【分析】根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角进行分析即可.
根据内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角进行分析即可.
【解答】解:∠1的同位角是∠2,∠5的内错角是∠6,
故选:B.
8.【分析】由折叠可得,∠DGH=∠DGE=74°,再根据AD∥BC,即可得到∠GHC=180°﹣∠DGH=106°.
【解答】解:∵∠AGE=32°,
∴∠DGE=148°,
由折叠可得,∠DGH=∠DGE=74°,
∵AD∥BC,
∴∠GHC=180°﹣∠DGH=106°,
故选:D.
9.【分析】直接根据平行线的性质即可得出结论.
【解答】解:∵AB∥CD,∠AEF=40°,
∴∠EFD=∠AEF=40°.
故选:B.
10.【分析】根据平行线的性质,知∠3的度数,再根据邻补角得出∠2=150°.
【解答】解:∵AB∥CD,∠1=30°,
∴∠3=∠1=30°,
又∵∠3+∠2=180°,
∴∠2=150°,
故选:C.
11.【分析】根据两直线平行,同位角相等,可得∠FAC=∠1,再根据角平分线的定义可得∠BAF=∠FAC.
【解答】解:∵DF∥AC,
∴∠FAC=∠1=35°,
∵AF是∠BAC的平分线,
∴∠BAF=∠FAC=35°,
故选:B.
12.【分析】设DE与AB相交于点F,由∠1=70°,可得∠AFE的度数,再根据平行线的性质,即可得到∠B的度数.
【解答】 解:设DE与AB相交于点F,
因为∠1=70°,
所以∠AFE=110°,
因为DE∥BC,
所以∠B=∠AFE=110°,
故选:C.
二.填空题(共6小题,满分24分,每小题4分)
13.【分析】直接利用垂直的定义结合互余以及互补的定义分析得出答案.
【解答】解:∵直线AB,CD相交于点O,EO⊥AB于点O,
∴∠EOB=90°,
∵∠EOD=50°,
∴∠BOD=40°,
则∠BOC的度数为:180°﹣40°=140°.
故答案为:140°.
14.【分析】根据垂线的定义,可得∠AOE的度数,根据余角的性质,可得∠AOC的度数,根据对顶角相等,可得答案.
【解答】解:由垂线的定义,得
∠AOE=90°,
由余角的性质,得
∠AOC=∠AOE﹣∠COE=30°,
由对顶角相等,得
∠BOD=∠AOC=30°,
故答案为:30.
15.【分析】同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,据此进行判断.
【解答】解:若∠A+∠ABC=180°,则BC∥AD;
若∠C+∠ADC=180°,则BC∥AD;
若∠CBD=∠ADB,则BC∥AD;
若∠C=∠CDE,则BC∥AD;
故答案为:∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE.(答案不唯一)
16.【分析】设另一个角为α,则这个角是4α﹣30°,然后根据两边分别平行的两个角相等或互补列式计算即可得解.
【解答】解:设另一个角为α,则这个角是4α﹣30°,
∵两个角的两边分别平行,
∴α+4α﹣30°=180°或α=4α﹣30°,
解得α=42°或α=10°,
∴4α﹣30°=138°或4α﹣30°=10°,
这两个角是42°,138°或10°,10°.
故答案为:42°,138°或10°,10°.
17.【分析】根据三角形的一个外角等于与它不相邻的两个内角的和,求出∠BCD,再根据两直线平行,内错角相等进行解答即可.
【解答】解:如图,∵∠E=34°,∠D=20°,
∴∠BCD=∠D+∠E=20°+34°=54°,
∵AB∥CD,
∴∠B=∠BCD=54°.
故答案为:54°.
18.【分析】根据三角形的一个外角等于与它不相邻的两个内角的和求出∠3,再根据两直线平行,同位角相等可得∠2=∠3.
【解答】解:如图,由三角形的外角性质得,∠3=90°+∠1=90°+36°=126°,
∵纸条的两边互相平行,
∴∠2=∠3=126°.
故答案为:126°.
三.解答题(共8小题,满分60分)
19.【分析】(1)依据平行线的性质,以及等量代换,即可得到∠HDE=∠HED.
(2)依据平行线的性质,即可得到∠DHE=90°,进而得出DG⊥EF.
【解答】解:(1)∠HDE=∠HED.理由如下:
∵DG∥AC(已知)
∴∠A=∠HDE(两直线平行,同位角相等)
∵EF∥BC(已知)
∴∠B=∠HED(两直线平行,同位角相等)
又∵∠A=∠B(已知)
∴∠HDE=∠HED( 等量代换).
(2)DG⊥EF.理由如下:
∵EF∥BC
∴∠AFE=∠C=90°
∵AC∥DG
∴∠DHE=∠AFE=90°
∴DG⊥EF.
故答案为:∠A,∠HDE,两直线平行,同位角相等;∠B,∠HED,两直线平行,同位角相等;∠HDE,∠HED,等量代换.DG⊥EF.
20.【分析】根据三角形内角和定理求出∠A,进而求出∠ACD=∠A,根据平行线的判定得出即可.
【解答】证明:∵∠B+∠1+∠A=180°,∠B=40°,∠A+10°=∠1,
∴40°+∠A+10°+∠A=180°,
∴∠A=65°,
∵∠ACD=65°,
∴∠ACD=∠A,
∴AB∥CD.
21.【分析】先利用角平分线定义得到∠3=∠ADC,∠2=∠ABC,而∠ABC=∠ADC,则∠3=∠2,加上∠1=∠2,则∠1=∠3,于是可根据平行线的判定得到DC∥AB.
【解答】证明:∵DE、BF分别是∠ABC,∠ADC的角平分线,
∴∠3=∠ADC,∠2=∠ABC,
∵∠ABC=∠ADC,
∴∠3=∠2,
∵∠1=∠2,
∴∠1=∠3,
∴DC∥AB.
22.【分析】先根据∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB得出∠DBC=∠ECB,再由∠DBC=∠F得出∠ECB=∠F,进而可得出结论.
【解答】证明:∵∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,
∴∠DBC=∠ABC,∠ECB=∠ACB,
∴∠DBC=∠ECB.
∵∠DBC=∠F,
∴∠ECB=∠F,
∴EC∥DF.
23.【分析】推出DG∥AC,根据平行线性质得出∠2=∠ACD,求出∠1=∠DCA,根据平行线判定推出即可.
【解答】证明:∵DG⊥BC,AC⊥BC,
∴∠DGB=∠ACB=90°(垂直定义),
∴DG∥AC(同位角相等,两直线平行),
∴∠2=∠ACD(两直线平行,内错角相等),
∵∠1=∠2,
∴∠1=∠DCA,
∴EF∥CD(同位角相等,两直线平行).
24.【分析】根据平行线的判定和性质解答即可.
【解答】解:∵EG∥HF
∴∠OEG=∠OFH,
∵∠1=∠2
∴∠AEF=∠DFE
∴AB∥CD,
∴∠BEF+∠DFE=180°.
25.【分析】根据外角的性质得到∠CFD=∠CDE﹣∠C=125°﹣45°=80°,根据平行线的性质得到∠BAC=∠DFC=80°,根据角平分线的定义得到∠FAD=∠BAC=40°,于是得到结论.
【解答】解:∵∠CDE=125°,∠C=45°,
∴∠CFD=∠CDE﹣∠C=125°﹣45°=80°,
∵AB∥EF,
∴∠BAC=∠DFC=80°,
∵AD平分∠BAC,
∴∠FAD=∠BAC=40°,
∴∠ADF=∠DFC﹣∠DAF=40°.
26.【分析】(1)延长EG交CD于H,根据平角的定义得到∠HGF=∠EGF=90°,根据平行线判定定理即可得到结论;
(2)延长EG交CD于H,根据平角的定义得到∠HGF=∠EGF=90°,根据平行线判定定理即可得到结论;
(3)根据平角的定义得到∠HGF=∠EGF=90°,根据平行线判定定理即可得到结论;
【解答】解:(1)AB∥CD,
理由:延长EG交CD于H,
∴∠HGF=∠EGF=90°,
∴∠GHF+∠GFH=90°,
∵∠BEG+∠DFG=90°,
∴∠BEG=∠GHF,
∴AB∥CD;
(2)∠BEG+∠MFD=90°,
理由:延长EG交CD于H,
∵AB∥CD,
∴∠BEG=∠GHF,
∵EG⊥FG,
∴∠GHF+∠GFH=90°,
∵∠MFG=2∠DFG,
∴∠BEG+∠MFD=90°;
(3)∠BEG+()∠MFD=90°,
理由:∵AB∥CD,
∴∠BEG=∠GHF,
∵EG⊥FG,
∴∠GHF+∠GFH=90°,
∵∠MFG=n∠DFG,
∴∠BEG+∠MFG=∠BEG+()∠MFD=90°.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2019/3/19 21:51:56;用户:教育人生;邮箱:1345206954@qq.com;学号:2050904
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
