第18课《思想文化》教案2(七年级下)
文档属性
| 名称 | 第18课《思想文化》教案2(七年级下) |

|
|
| 格式 | rar | ||
| 文件大小 | 12.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 历史 | ||
| 更新时间 | 2010-01-28 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
走进数学世界
1.2我们周围的“数”
车牌中的学问
想一想
(1) 当“京B”后面的五个数位上 都是数字时,可以有多少个不同 的汽车牌照号?
牌照号从00000到99999 可供100000辆汽车使用.
车牌中的学问
想一想
(2)现在北京市一些汽车牌照号 五个数位中,后四位上都是数字, 而第一个数位上有数字,有大写 英文字母.你知道为什么这样做吗?
不同的汽车牌号数将增加
车牌中的学问
想一想
(3)这样做以后,最多可以有多少个不同的汽车牌照号?
不同的汽车牌号数将增加到 36×10000=360000
九宫图
将1,2,3,…,9这九个 数字分别填入图中的九个方格内, 使每行、每列和对角线上的三个
格内的数字之和分别等于15. 怎样完成这个游戏?
试一试
5
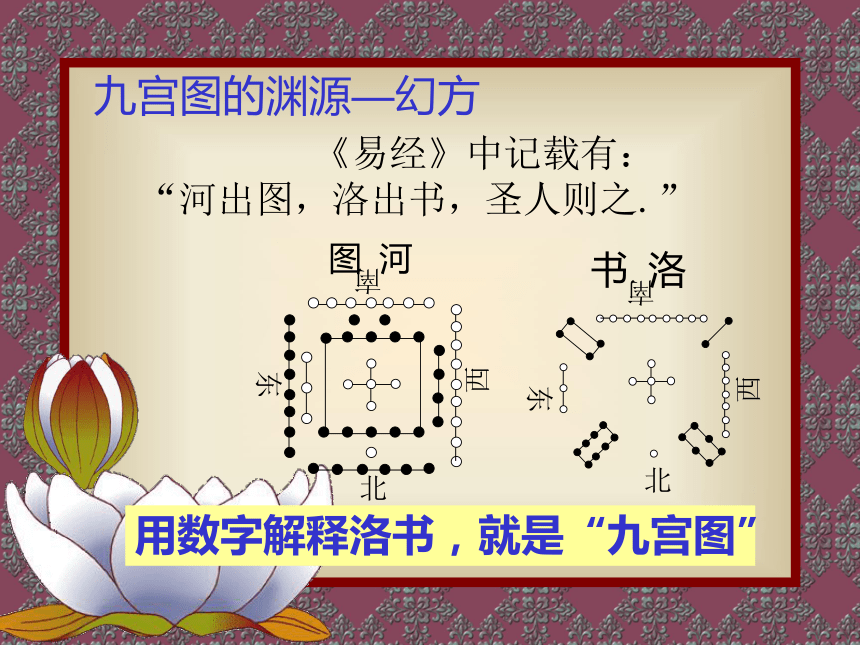
图 河
西
东
南
北
《易经》中记载有: “河出图,洛出书,圣人则之.”
西
东
南
北
书 洛
九宫图的渊源—幻方
用数字解释洛书,就是“九宫图”
在6世纪,北周的数学家甄鸾 就是这样描述它的:“九宫者, 二四为肩,六八为足,左三右七, 戴九履一,五居中央.”
1
2
3
4
5
6
7
8
9
二四为肩
六八为足
左三右七
填法 之一
到了1275年,南宋的数学家杨辉 在《续古摘奇算法》中介绍了 “九宫图”的填法:“九子斜排,
1
2
3
4
5
6
7
8
9
上下对易,左右相更,四维挺出.”
填法 之二
在4世纪时才有希腊人关于 “4阶”纵横图的记载,9世纪时 才有伊拉克人柯拉(Korra)来 研究纵横图.在欧洲,到了1514年 才出现了第一幅完整的纵横图.
4阶纵横图
想一想:你能根据提示在图中填出 “4阶”纵横图吗?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.把1-16依次排列
提示:
2.把箭头所指的 两数互易
3.填写结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
每行每列的数字之和是 ?
34
试一试选择几种圆形的物体,想办法 度量它们的直径与周长,并填写下表:
周长
直径 周长与直径
的比值
物体1
物体2
物体3
物体4
人类为了探求圆周率究竟 是什么数,付出了长期艰苦的 努力.我国古代著名数学家祖 冲之(公元429—公元500) 在计算工具十分简陋的年代,将圆周率 确定在3.1415926到3.1415927之间,
这个精确到小数点后面7位的数值在 世界上领先了1000多年,是中国古代 数学家对人类文明的重大贡献.
有关“数”的历史—圆周率
课堂小结
1. 我们的生活离不开“数”
2.“数”可以做游戏
3.“数”可以做实验
4.中国古代数学家对人类 文明做出重大贡献.
走进数学世界
1.2我们周围的“数”
车牌中的学问
想一想
(1) 当“京B”后面的五个数位上 都是数字时,可以有多少个不同 的汽车牌照号?
牌照号从00000到99999 可供100000辆汽车使用.
车牌中的学问
想一想
(2)现在北京市一些汽车牌照号 五个数位中,后四位上都是数字, 而第一个数位上有数字,有大写 英文字母.你知道为什么这样做吗?
不同的汽车牌号数将增加
车牌中的学问
想一想
(3)这样做以后,最多可以有多少个不同的汽车牌照号?
不同的汽车牌号数将增加到 36×10000=360000
九宫图
将1,2,3,…,9这九个 数字分别填入图中的九个方格内, 使每行、每列和对角线上的三个
格内的数字之和分别等于15. 怎样完成这个游戏?
试一试
5
图 河
西
东
南
北
《易经》中记载有: “河出图,洛出书,圣人则之.”
西
东
南
北
书 洛
九宫图的渊源—幻方
用数字解释洛书,就是“九宫图”
在6世纪,北周的数学家甄鸾 就是这样描述它的:“九宫者, 二四为肩,六八为足,左三右七, 戴九履一,五居中央.”
1
2
3
4
5
6
7
8
9
二四为肩
六八为足
左三右七
填法 之一
到了1275年,南宋的数学家杨辉 在《续古摘奇算法》中介绍了 “九宫图”的填法:“九子斜排,
1
2
3
4
5
6
7
8
9
上下对易,左右相更,四维挺出.”
填法 之二
在4世纪时才有希腊人关于 “4阶”纵横图的记载,9世纪时 才有伊拉克人柯拉(Korra)来 研究纵横图.在欧洲,到了1514年 才出现了第一幅完整的纵横图.
4阶纵横图
想一想:你能根据提示在图中填出 “4阶”纵横图吗?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.把1-16依次排列
提示:
2.把箭头所指的 两数互易
3.填写结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
每行每列的数字之和是 ?
34
试一试选择几种圆形的物体,想办法 度量它们的直径与周长,并填写下表:
周长
直径 周长与直径
的比值
物体1
物体2
物体3
物体4
人类为了探求圆周率究竟 是什么数,付出了长期艰苦的 努力.我国古代著名数学家祖 冲之(公元429—公元500) 在计算工具十分简陋的年代,将圆周率 确定在3.1415926到3.1415927之间,
这个精确到小数点后面7位的数值在 世界上领先了1000多年,是中国古代 数学家对人类文明的重大贡献.
有关“数”的历史—圆周率
课堂小结
1. 我们的生活离不开“数”
2.“数”可以做游戏
3.“数”可以做实验
4.中国古代数学家对人类 文明做出重大贡献.
同课章节目录
- 第一单元 繁荣与开放的社会
- 第1课 统一国家的重建
- 第2课 唐太宗与贞观之治
- 第3课 从武周政治到开元盛世
- 第4课 唐代的边疆各族
- 第5课 唐代的中外文化交流
- 第6课 文成公主与西藏——探究活动(一)
- 第二单元 经济重心的南移和民族关系的发展
- 第7课 辽、宋、西夏、金并立
- 第8课 经济重心的南移
- 第9课 宋代的城市生活
- 第10课 元朝的统一
- 第11课 宋代的社会生活——探究活动(二)
- 第三单元 统一多民族国家的巩固和社会危机
- 第12课 明清两朝的专制统治
- 第13课 抗击侵略的英雄业绩
- 第14课 广阔疆域上的统一国家
- 第15课 中外经济文化交流
- 第16课 闭关锁国
- 第17课 郑成功收复台湾——探究活动(三)
- 第四单元 思想文化与科学技术
- 第18课 思想文化
- 第19课 文学艺术(上)
- 第20课 文学艺术(下)
- 第21课 科学技术(上)
- 第22课 科学技术(下)
- 第23课 印刷术——探究活动(四)
