2018-2019学年重庆外国语学校九年级(下)开学数学试卷(解析版)
文档属性
| 名称 | 2018-2019学年重庆外国语学校九年级(下)开学数学试卷(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 301.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-22 00:00:00 | ||
图片预览




文档简介
2018-2019学年重庆外国语学校九年级(下)开学数学试卷
一、选择题(本大题共12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A,B,C,D的四个答案,其中只有一个是正确的,请将正确的答案的代号在答题卡中对应的方框涂黑。
1.(4分)四个实数0、、﹣3.14、﹣2中,最小的数是( )
A.0 B. C.﹣3.14 D.﹣2
2.(4分)下列汽车标志中,可以看作是中心对称图形的是( )
A. B.
C. D.
3.(4分)下列调查方式中适合的是( )
A.为了了解市民对电影《南京南京》的感受,小华在某校随机采访了8名初三学生
B.为了了解全校学生用于做数学作业的时间,小民同学在网上向3位好友做了调查
C.为了了解某段水域的水质情况,环保部门采用了抽样调查的方式
D.为了了解全市中学生每天的就寝时间,调查人员采用了普查的方式
4.(4分)观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2019个图形共有( )个〇.
A.6055 B.6056 C.6057 D.6058
5.(4分)如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
A.= B.= C.= D.=
6.(4分)下列命题是真命题的有( )个
①一组对边相等的四边形是矩形;②两条对角线相等的四边形是矩形;③四条边都相等且对角线互相垂直的四边形是正方形;④四条边都相等的四边形是菱形;⑤一组邻边相等的矩形是正方形.
A.1 B.2 C.3 D.4
7.(4分)估计(2﹣1)的值应在( )
A.16和17之间 B.17和18之间 C.18和19之间 D.20和21之间
8.(4分)小明按如图所示的程序输入一个正数x,最后输出的结果为597,则满足条件的x的不同值最多有( )
A.4个 B.5个 C.6个 D.无数个
9.(4分)如果,AB是⊙O的切线,A为切点,OB=5,AB=5,AC是⊙O的弦,OH⊥AC,垂足为H,若OH=3,则弦AC的长为( )
A.5 B.6 C.8 D.10
10.(4分)某游乐场推出了一个“极速飞车”的项目,项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯AB自由上下选择项目难度,其中斜坡轨道BC的坡度(或坡比)为i=1:2,BC=24米,CD=10米,∠D=36°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.(精确到0.1米,参考数据:tan36°≈0.73,cos36°≈0.81,sin36°≈0.59)
A.13.8 B.18.3 C.24.3 D.42.3
11.(4分)如图,点A、B为双曲线y=(x>0)上两点,AC⊥x轴于点C,BD⊥y轴于点D,交AC于点E,当AD∥OE时,矩形OCED面积为,则k的值为( )
A.3 B. C.4 D.5
12.(4分)若函数y=(a﹣2)x2﹣2ax+a﹣与x轴有交点,且关于x的不等式组无解,则符合条件的整数a的值有( )个
A.3 B.4 C.5 D.6
二、填空题:(本大题共6个小题,每小题4分,共24分)请把下列各题的正确答案填写在答题卡中对应的横线上.
13.(4分)计算:+(﹣2018)0﹣4sin45°+|﹣2|= .
14.(4分)如图,在Rt△ABC中,∠C=90°,CA=CB=2.分别以A、B、C为圆心,以AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是 .(保留π)
15.(4分)现将背面完全相同,正面分别标有数﹣6、1、2、3的4张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数标记为m,再从剩下的3张卡片中任取一张,将该卡片上的数记为n,则数字m、n都不是方程x2﹣5x+6=0的解的概率为 .
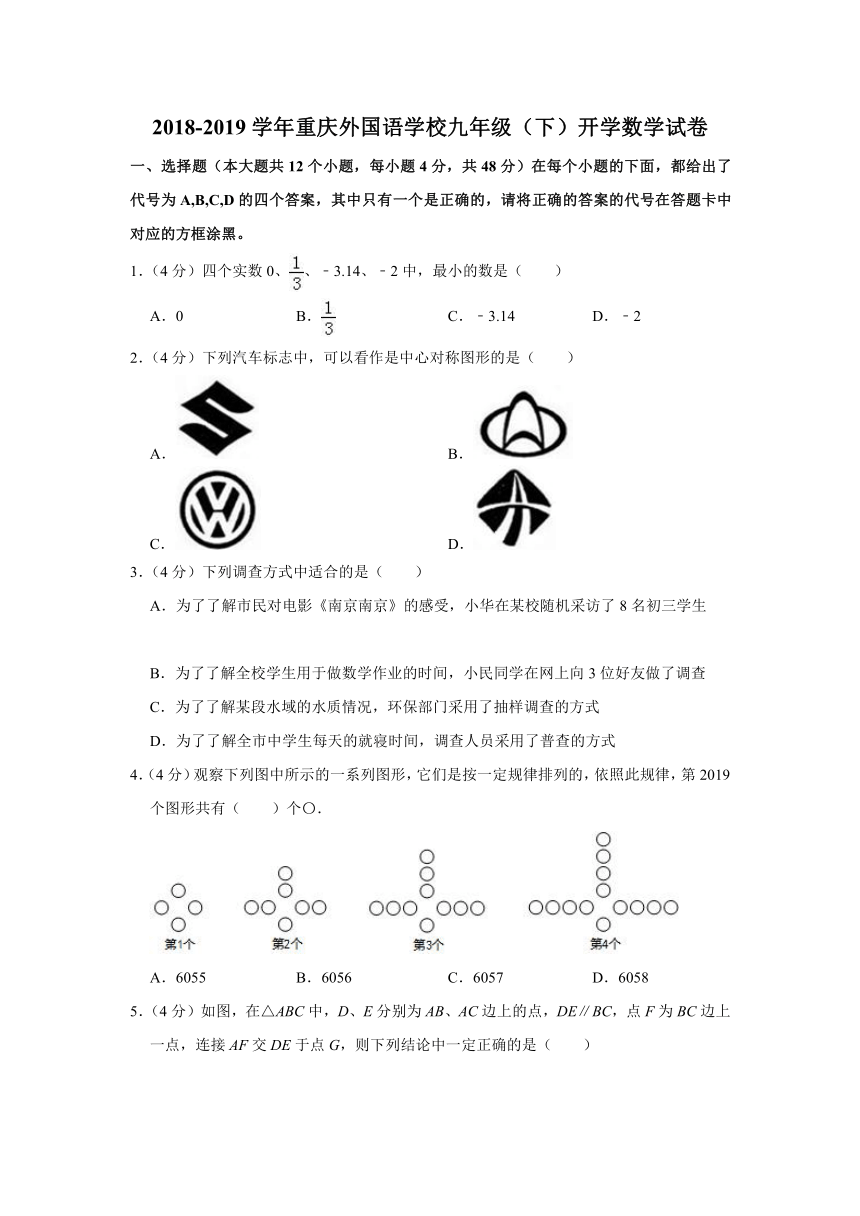
16.(4分)如图,以矩形OABC的顶点O为原点,OA为x轴,OC为y轴建立平面直角坐标系,双曲钱y=与AB、BC分别交于点D、E,沿直线DE将△DBE翻折得△DFE,且点F恰好落在直线OA上,若AB:BC=4:5,则矩形的面积是 .
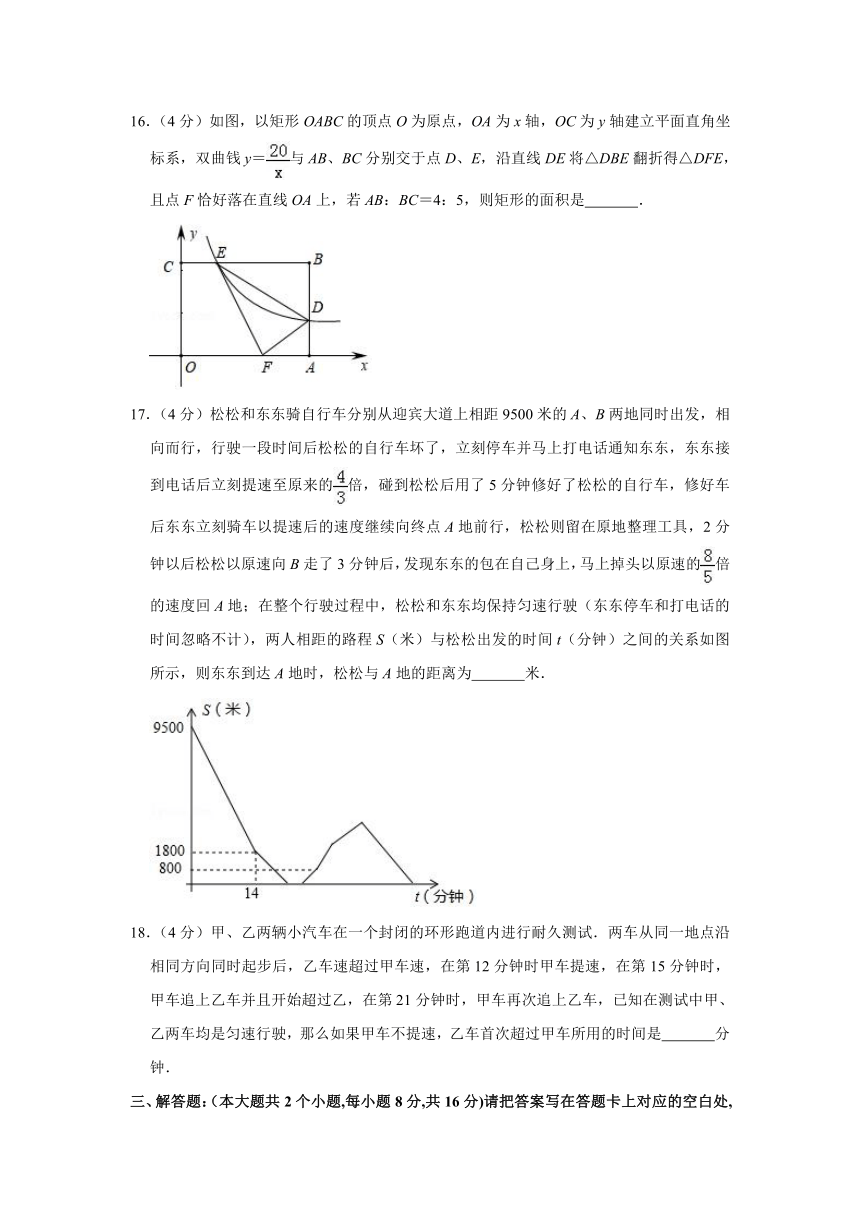
17.(4分)松松和东东骑自行车分别从迎宾大道上相距9500米的A、B两地同时出发,相向而行,行驶一段时间后松松的自行车坏了,立刻停车并马上打电话通知东东,东东接到电话后立刻提速至原来的倍,碰到松松后用了5分钟修好了松松的自行车,修好车后东东立刻骑车以提速后的速度继续向终点A地前行,松松则留在原地整理工具,2分钟以后松松以原速向B走了3分钟后,发现东东的包在自己身上,马上掉头以原速的倍的速度回A地;在整个行驶过程中,松松和东东均保持匀速行驶(东东停车和打电话的时间忽略不计),两人相距的路程S(米)与松松出发的时间t(分钟)之间的关系如图所示,则东东到达A地时,松松与A地的距离为 米.
18.(4分)甲、乙两辆小汽车在一个封闭的环形跑道内进行耐久测试.两车从同一地点沿相同方向同时起步后,乙车速超过甲车速,在第12分钟时甲车提速,在第15分钟时,甲车追上乙车并且开始超过乙,在第21分钟时,甲车再次追上乙车,已知在测试中甲、乙两车均是匀速行驶,那么如果甲车不提速,乙车首次超过甲车所用的时间是 分钟.
三、解答题:(本大题共2个小题,每小题8分,共16分)请把答案写在答题卡上对应的空白处,解答时每小题必须给出必要的演算过程或推理步骤。
19.(8分)如图,AB∥CD,点E在AB上,点F在CD上,连接EF,EH平分∠BEF,交CD于点H,过F作FG⊥EF,交EH于点G,若∠G=32°,求∠HFG的度数.
20.(8分)某市为提高环境质量对全市的环境污染进行综合治理,在治理的过程中环保部门随机选取了平安镇和富贵镇进行空气质量监测.
过程如下,请补充完整.
收集数据:
从2017年12月初开始连续一年对两镇的空气质量进行监测,将30天的空气污染指数(简称API)的平均值作为每个月的空气污染指数,12个月的空气污染指数如下:
平安镇:120 115 45 100 95 50 80 70 85 50 50 100
富贵镇:110 90 105 80 90 85 90 50 90 45 70 60
(1)整理、描述数据:
按下表整理、描述这两镇空气污染指数的数据:
空气质量为优
空气质量为良
空气质量为轻微污染
平安镇
4
6
2
富贵镇
(说明空气污染指数<50时,空气质量为优;50≤空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻度污染)
(2)分析数据:
两镇的空气污染指数的平均数、中位数、众数如表所示:
城镇
平均数
中位数
众数
平安镇
80
50
富贵镇
81.3
87.5
请将以上两个表格补充完整;
(3)得出结论:可以推断出 镇这一年中环境状况比较好,理由: .(至少从两个不同的角度说明推断的合理性)
四、解答题(本大题4个小题,每小题10分,共40分)解答时每小题都必须写出必要的演算过程或推理步骤,请将解答过程书写在答题卡中对应的位置上。
21.(10分)计算:
(1)(a+b)(a﹣b)﹣(a+b)2
(2)(+x﹣1)
22.(10分)如图,在平面直角坐标系中,直线l1与x轴交于点B,与y轴交于点C,直线l1与直线l2:y=x交于点A,将直线l2:y=x沿射线AB的方向平移得到直线l3,当l3经过点B时,与y轴交点记为D点,已知A点的纵坐标为﹣2,sin∠ABO=.
(1)求直线BC的解析式;
(2)求△ABD的面积.
23.(10分)某商店2月购进了甲乙两种货物共300千克,已知甲进价每千克20元,售价每千克40元,乙进价每千克5元,售价每千克10元.
(1)若这批货物全部销售完获利不低于4500元,则甲至少购进多少千克?
(2)第一批货物很快售完,于是商家决定购进第二批甲和乙两种货物,甲和乙的进价不变,经调查发现甲售价每上涨2元,销量比(1)中获得最低利润时的销量下降5千克:乙每千克售价比第一批上涨1.2元,销量与(1)中获得最低利润的销量保持不变,结果第二批中已经卖掉的甲和乙的销售总额比(1)中第一批甲和乙售完后对应的最低销售总额增加了480元,求第二批货物中甲的售价.
24.(10分)在平行四边形ABCD中,∠ABE=45°,点E在对角线AC上,BE的延长线交CD于点F,交AD的延长线于点G,过点C作CH⊥AB于点H,交BF于点M.
(1)若BE=3,AE=,求△ABE的面积;
(2)若∠ABC=3∠EBC.CA=CB,求证:CM=FG.
五、解答题(本大题2个小题,25题10分,26题12分,共22分)解答时每小题都必须写出必要的演算过程成推理步骤,请将解答过程书写在答题卡中对应的位置上。
25.(10分)我国著名的数学家秦九韶在《数书九章》提出了“三斜求积术”.即已知三角形的三边长,求它的面积.
用现代式子表示即为s=……①(其中a,b,c为三角形的三边长,s为面积.)
而另一个文明古国古希腊也有求三角形面积的海伦公式:
s=…②(其中a,b,c为三角形的三边长,p=)
(1)若已知三角形的三边长分别为5、7、8,请在上述两种公式中选择一种你喜欢的公式,计算该三角形的面积;
(2)事实上,“三斜求积术”与海伦公式是等价的,可以由“三斜求积术”直接推导出海伦公式,其部分推导过程如下:
∵[a2b2﹣()2]=[4a2b2﹣(a2+b2﹣c2)2]
=…
请将上述推导过程补充完整;
(3)如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1,以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x,试利用海伦公式求△ABC的最大面积.
26.(12分)二次函数y=﹣x2图象与x轴交于A、B两点,与y轴交于点C,连接AC、BC.
(1)如图1,求△ABC的周长;
(2)如图2,D为线段AB上一动点,作DE∥BC交AC于点E,当△CDE面积最大时,过E作x轴的平行线,交y轴于点F,交BC于点H,点P为线段FH上一动点,将△CFH绕点C沿逆时针方向旋转90°,点F,P,H的对应点分别是F′,P′,H′,点Q从点P出发,先沿适当的路径运动到点F′处,再沿F′C运动到点C处,最后沿适当的路径运动到点P′处停止,求点Q经过的最短路径的长是多少;
(3)如图3,点M是点C关于x轴的对称点,N是线段OB上一动点,经过MN的直线与抛物线交于点G,将△AMG沿MN翻折,点A的对应点是A′,是否存在点A′,使得△CBA′是等腰三角形,若存在求出点A′的坐标,若不存在,请说明理由.
2018-2019学年重庆外国语学校九年级(下)开学数学试卷
参考答案与试题解析
一、选择题(本大题共12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A,B,C,D的四个答案,其中只有一个是正确的,请将正确的答案的代号在答题卡中对应的方框涂黑。
1.【解答】解:∵﹣3.14<﹣2<0<,
∴四个实数0、、﹣3.14、﹣2中,最小的数是﹣3.14.
故选:C.
2.【解答】解:A.旋转180°,与原图形能够完全重合是中心对称图形;故此选项正确;
B.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项错误;
C.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项错误;
D.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项错误;
故选:A.
3.【解答】解:为了了解市民对电影《南京南京》的感受,小华在某校随机采访了8名初三学生不合适;
为了了解全校学生用于做数学作业的时间,小民同学在网上向3位好友做了调查不合适;
为了了解某段水域的水质情况,环保部门采用了抽样调查的方式,合适;
为了了解全市中学生每天的就寝时间,调查人员采用了普查的方式不合适;
故选:C.
4.【解答】解:设第n个图形有an个〇(n为正整数),
观察图形,可知:a1=1+3×1,a2=1+3×2,a3=1+3×3,a4=1+3×4,…,
∴an=1+3n(n为正整数),
∴a2019=1+3×2019=6058.
故选:D.
5.【解答】解:(A)∵DE∥BC,
∴△ADE∽△ABC,
∴,故A错误;
(B)∵DE∥BC,
∴,故B错误;
(C)∵DE∥BC,
,故C正确;
(D)∵DE∥BC,
∴△AGE∽△AFC,
∴=,故D错误;
故选:C.
6.【解答】解:①一组对边相等的四边形不一定是矩形,错误;
②两条对角线相等的平行四边形是矩形,错误;
③四条边都相等且对角线互相垂直的四边形是正方形,正确;
④四条边都相等的四边形是菱形,正确;
⑤一组邻边相等的矩形是正方形,正确.
故选:C.
7.【解答】解:∵9<11<16,
∴3<<4,即﹣4<﹣<﹣3,
∴18<22﹣<19,即18<(2﹣1)<19,
故选:C.
8.【解答】解:若4x+1=597,则有x=149,
若4x+1=149,则有x=37,
若4x+1=37,则有x=9,
若4x+1=9,则有x=2,
若4x+1=2,则有x=,
则满足条件的x不同值最多有5个,
故选:B.
9.【解答】解:∵AB是⊙O的切线,A为切点,
∴OA⊥AB,
∴∠OAB=90°,
∴OA===5,
∵OH⊥AC,
∴AH=CH,
在Rt△AOH中,AH==4.
∴AC=2AH=8.
故选:C.
10.【解答】解:如图
,
由斜坡轨道BC的坡度(或坡比)为i=1:2,得
BE:CE=1:2.
设BE=xm,CE=2xm.
在Rt△BCE中,由勾股定理,得
BE2+CE2=BC2,
即x2+(2x)2=(24)2,
解得x=24,
BE=24m,CE=48m,
DE=DC+CE=10+48=58m,
由tan36°≈0.73,得=0.73,
解得AB=0.73×58=42.34m.
由线段的和差,得
AB=AE﹣BE=42.34﹣24=18.34≈18.3m,
故选:B.
11.【解答】解:∵AD∥OE,AE∥OD,
∴四边形ADOE是平行四边形,
∴OD=AE,
又∵OD=CE,
∴AE=CE,
∴AC=2CE,
∴S矩形OCED=S△OAC,
∴S=|k|=,
又∵k>0,
∴k=5.
故选:D.
12.【解答】解:,
解不等式①得:x≤a,
解不等式②得:x>5,
∵关于x的不等式组无解,
∴a≤5.
①当二次函数y=(a﹣2)x2﹣2ax+a﹣与x轴有交点时,
方程(a﹣2)x2﹣2ax+a﹣=0的△=(﹣2a)2﹣4(a﹣2)(a﹣)≥0,
解得:a≥,
∴≤a≤5.
又∵a≠2,
整数有1,3,4,5,共4个.
②当函数y=(a﹣2)x2﹣2ax+a﹣是一次函数时,a﹣2=0,此时a=2.
综上所述,整数有1,2,3,4,5,共5个.
故选:C.
二、填空题:(本大题共6个小题,每小题4分,共24分)请把下列各题的正确答案填写在答题卡中对应的横线上.
13.【解答】解:+(﹣2018)0﹣4sin45°+|﹣2|
=2+1﹣4×+2
=2+1﹣2+2
=3.
故答案为:3.
14.【解答】解:2×2÷2﹣﹣=2﹣.
15.【解答】解:画树状图如下:
由树状图知共有12种等可能结果,
∵x2﹣5x+6=0的解为x=2或x=3,
∴数字m、n都不是方程x2﹣5x+6=0的解的有2种结果,
所以数字m、n都不是方程x2﹣5x+6=0的解的概率为=,
故答案为:.
16.【解答】解:根据AB:BC=4:5,设AB=4t,则有BC=5t,即A(5t,0),B(5t,4t),
∵E、D为反比例函数y=与BC、BA的交点,
∴D(5t,),E(,4t),
∵直线DE将△DBE翻折得△DFE,且点F恰好落在直线OA上,
∴BF⊥DE,BF的中点在DE上,
∵直线DE的斜率为=﹣,方程为y﹣4t=﹣(x﹣),
∴直线BF斜率为,
∴直线BF解析式为y﹣4t=(x﹣5t),即y=x﹣t,
令y=0,得到x=t,即F( t,0),
∴BF的中点坐标为( ,2t),
将中点坐标代入直线DE解析式得:2t﹣4t=﹣(﹣),
整理得:t2=,
则S矩形=5t?4t=20t2=.
故答案为:.
17.【解答】解:由题意:14分钟两人走了9500﹣1800=7700米(图中两人分别到了C,D)
∴两人的速度和为550米/分钟,
提速后东东的速度为800÷2=400米/分钟,
∴东东原来的速度=400÷=300米/分钟,
∴松松的速度为250米/分钟,
∴AC=250×14=3500米,BD=14×300=4200米,
设2分钟以后松松以原速向B走了3分钟到达点G,
∴修好车后东东到达A是时间为:=8.75分钟,此时松松到达点H,
∴东东到达A地时,松松与A地的距离HG=AC+CG﹣HG=3500+3×250﹣(8.75﹣2﹣3)×250×=2750米.
故答案为2750.
18.【解答】解:方法一:设甲车提速前速度比乙车慢a/分钟,提速后速度比乙车快b/分钟.
那么有甲车在第12分钟时,离乙车的距离为12a.这个距离在第15分钟追回来.
那么12a=(15﹣12)b.即b=4a,
而且在第21分钟时,甲车比乙车多跑一圈.
那么一圈的路程为(21﹣15)b=6b=24a,
所以甲车不提速时,乙车首次超过甲车(即多跑一圈)所需时间为:24a÷a=24分钟,
故答案为:24.
方法二:设甲车提速前的速度为x1,提速后的速度为x2,乙车的速度为y,
根据第12分钟时甲车提速,可得:3(x2﹣y)=12(y﹣x1),
化简得:(x2﹣y)=4(y﹣x1)①,
根据在第21分钟时,甲车再次追上乙车,可得:6(x2﹣y)=1,
化简,得:x2﹣y=②,
由①②可得:4(y﹣x1)=,
解得:y﹣x1=,
所以甲车不提速时,乙车首次超过甲车(即多跑一圈)所需时间为:=24.
故答案为:24.
三、解答题:(本大题共2个小题,每小题8分,共16分)请把答案写在答题卡上对应的空白处,解答时每小题必须给出必要的演算过程或推理步骤。
19.【解答】解:如图所示,∵FG⊥EF,∠G=32°,
∴∠GEF=58°,
∵EH平分∠BEF,
∴∠BEH=58°,
∵AB∥CD,
∴∠DHG=∠BEG=58°,
∴∠HFG=∠DHG﹣∠G=58°﹣32°=26°.
20.【解答】解:(1)富贵镇空气质量为优的天数是1天;空气质量为良的天数为9天;空气质量为轻微污染的天数为2天;
故答案为:1,9,2
(2)平安镇:120 115 100 100 95 85 80 70 50 50 50 45,
其中位于中间的两个数是85和80,所以其中位数为=82.5;
富贵镇的数据中,90出现了四次,出现的次数最多,故其众数为90.
故答案为82.5,90.
(3)平安镇的环境状况较好.
例如:平安镇空气质量优的天数多于富贵镇,平安镇的污染指数的平均数小于富贵镇或平安镇空气污染指数的众数是50,属于空气质量优,而富贵镇空气污染指数的众数是90,属于轻微污染等;
故答案为:平安镇;平安镇空气质量优的天数多于富贵镇,平安镇的污染指数的平均数小于富贵镇或平安镇空气污染指数的众数是50,属于空气质量优,而富贵镇空气污染指数的众数是90,属于轻微污染等.
四、解答题(本大题4个小题,每小题10分,共40分)解答时每小题都必须写出必要的演算过程或推理步骤,请将解答过程书写在答题卡中对应的位置上。
21.【解答】解:(1)(a+b)(a﹣b)﹣(a+b)2
=a2﹣b2﹣(a2+2ab+b2)
=﹣2b2﹣2ab;
(2)(+x﹣1)
=[+]×
=×
=×
=.
22.【解答】解:(1)∵点A的纵坐标为﹣2且在直线l2:y=x上
∴x=﹣2 解得:x=﹣4
∴A(﹣4,﹣2)
过A作AH⊥x轴于H,如图,则AH=2,OH=4
sin∠ABO==
∴AB=
∴BH===3
∴OB=OH+BH=7 即B(﹣7,0)
设直线BC解析式为y=kx+b,得:
解得:
∴直线BC解析式为y=﹣x﹣
(2)延长AH交BD于G,如图,
∵将直线l2:y=x平移得到直线l3
∴设直线l3:y=x+d,经过点B(﹣7,0)
解得d= 即D(0,),OD=
∵AG∥OD,AO∥DG
∴四边形AODG是平行四边形
∴AG=OD=
∴S△ABD=S△ABG+S△ADG
=AG?BH+AG?OH
=AG?OB
=
=
∴△ABD的面积为
23.【解答】解:(1)设购进甲x千克,则购进乙(300﹣x)千克,
根据题意得:(40﹣20)x+(10﹣5)(300﹣x)≥4500,
解得:x≥200.
答:甲至少购进200千克;
(2)设第二批货物中甲的售价为a,
根据题意得:a×[200﹣5(a﹣40)÷2]+(10+1.2)(300﹣200)=40×200+10×(300﹣200)+480,
整理得:a2﹣120a+1024=0,
解得:a1=44,a2=76(不合题意,舍去).
答:第二批货物中甲的售价为44.
24.【解答】解:(1)过E作EN⊥AB于N,
∵∠ABE=45°,
∴△BEN是等腰直角三角形,
∴BN=EN=BE=3,
∵AE=,
∴AN==1,
∴AB=4,
∴△ABE的面积=×4×3=6;
(2)∵∠ABE=45°,∠ABC=3∠EBC,
∴∠ABC=67.5°,
∵CA=CB,CH⊥AB,
∴∠CAB=∠CBA=67.5°,∠BCH=∠ACH=22.5°,
∴∠CME=∠BMH=∠MBH=45°,
∴∠CEM=112.5°,
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠FDG=∠BAD=112.5°,∠GFD=∠EBA=45°,
∴∠GFD=∠CME,∠FDG=∠MEC,
∵∠BCM=∠CBM=22.5°,
∴CM=BM,
∵∠BEA=∠EAB=67.5°,
∴BE=AB,
∴BE=CD,
在等腰直角三角形CMF中,
∵∠CMF=∠AFM=45°,
∴CM=CF,
∴BM=CF,
∴EM=DF,
在△MEC与△FDG中,,
∴△MEC≌△FDG(ASA),
∴CM=FG.
五、解答题(本大题2个小题,25题10分,26题12分,共22分)解答时每小题都必须写出必要的演算过程成推理步骤,请将解答过程书写在答题卡中对应的位置上。
25.【解答】(1)由题意,得 a=5,b=7,c=8,
∴p=,
∴△ABC面积=.
(2)∵s2=)]=
=
=p(p﹣a)(p﹣b)(p﹣c),
∴s=;
(3)由旋转性质得AC=MA=1,BC=BN=3﹣x,AB=x,p=2,
代入海伦公式,得△ABC的面积=,
∴当x=时,△ABC的面积最大,为.
26.【解答】解:(1)当x=0时,y=2,
∴C(0,2),
当y=0时,﹣x2=0,
解得:x=﹣或4,
∴A(﹣,0),B(4,0),
∴AB=5,
∵AC2==15,BC2==60,
∴△ABC的周长=AB+AC+BC=5++2=5+3;
(2)如图2,由(1)得:AC2+BC2=AB2,
∴∠ACB=90°,
∵DE∥BC,
∴∠AED=90°,
∵tan∠CAD====2,
设AE=m,ED=2m,AD=m,
∴CE=﹣m,
S△CED===﹣m2+m=﹣(m﹣)2+,
∴当m=时,即E是AC中点,△CDE面积最大,
连接OF',交EH于点P,连接CP,则CP=OP,
由旋转得:CP'=CP,
∴CP=OP=CP',
所以PF'+CF'+CP'=PF'+OP+CF'=OF'+CF'=+=+,
则点Q经过的最短路径的长是+;
(3)存在,分三种情况:
设A'(x,y),
①当A'C=A'B时,如图4,
∵A'C=A'B,AM=A'M,
∴,
解得:x=或(舍),
∴A'(,);
②当BC=CA'时,如图5,
∵AM=A'M,
∴,
解得:x=,y=﹣,
∴A'(,﹣);
③当BC=A'B时,如图6,
∵AM=A'M,
∴,
解得:x=或(舍),
A'(,),
综上,点A'的坐标为(,)或(,﹣)或(,).
一、选择题(本大题共12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A,B,C,D的四个答案,其中只有一个是正确的,请将正确的答案的代号在答题卡中对应的方框涂黑。
1.(4分)四个实数0、、﹣3.14、﹣2中,最小的数是( )
A.0 B. C.﹣3.14 D.﹣2
2.(4分)下列汽车标志中,可以看作是中心对称图形的是( )
A. B.
C. D.
3.(4分)下列调查方式中适合的是( )
A.为了了解市民对电影《南京南京》的感受,小华在某校随机采访了8名初三学生
B.为了了解全校学生用于做数学作业的时间,小民同学在网上向3位好友做了调查
C.为了了解某段水域的水质情况,环保部门采用了抽样调查的方式
D.为了了解全市中学生每天的就寝时间,调查人员采用了普查的方式
4.(4分)观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2019个图形共有( )个〇.
A.6055 B.6056 C.6057 D.6058
5.(4分)如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
A.= B.= C.= D.=
6.(4分)下列命题是真命题的有( )个
①一组对边相等的四边形是矩形;②两条对角线相等的四边形是矩形;③四条边都相等且对角线互相垂直的四边形是正方形;④四条边都相等的四边形是菱形;⑤一组邻边相等的矩形是正方形.
A.1 B.2 C.3 D.4
7.(4分)估计(2﹣1)的值应在( )
A.16和17之间 B.17和18之间 C.18和19之间 D.20和21之间
8.(4分)小明按如图所示的程序输入一个正数x,最后输出的结果为597,则满足条件的x的不同值最多有( )
A.4个 B.5个 C.6个 D.无数个
9.(4分)如果,AB是⊙O的切线,A为切点,OB=5,AB=5,AC是⊙O的弦,OH⊥AC,垂足为H,若OH=3,则弦AC的长为( )
A.5 B.6 C.8 D.10
10.(4分)某游乐场推出了一个“极速飞车”的项目,项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯AB自由上下选择项目难度,其中斜坡轨道BC的坡度(或坡比)为i=1:2,BC=24米,CD=10米,∠D=36°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.(精确到0.1米,参考数据:tan36°≈0.73,cos36°≈0.81,sin36°≈0.59)
A.13.8 B.18.3 C.24.3 D.42.3
11.(4分)如图,点A、B为双曲线y=(x>0)上两点,AC⊥x轴于点C,BD⊥y轴于点D,交AC于点E,当AD∥OE时,矩形OCED面积为,则k的值为( )
A.3 B. C.4 D.5
12.(4分)若函数y=(a﹣2)x2﹣2ax+a﹣与x轴有交点,且关于x的不等式组无解,则符合条件的整数a的值有( )个
A.3 B.4 C.5 D.6
二、填空题:(本大题共6个小题,每小题4分,共24分)请把下列各题的正确答案填写在答题卡中对应的横线上.
13.(4分)计算:+(﹣2018)0﹣4sin45°+|﹣2|= .
14.(4分)如图,在Rt△ABC中,∠C=90°,CA=CB=2.分别以A、B、C为圆心,以AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是 .(保留π)
15.(4分)现将背面完全相同,正面分别标有数﹣6、1、2、3的4张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数标记为m,再从剩下的3张卡片中任取一张,将该卡片上的数记为n,则数字m、n都不是方程x2﹣5x+6=0的解的概率为 .
16.(4分)如图,以矩形OABC的顶点O为原点,OA为x轴,OC为y轴建立平面直角坐标系,双曲钱y=与AB、BC分别交于点D、E,沿直线DE将△DBE翻折得△DFE,且点F恰好落在直线OA上,若AB:BC=4:5,则矩形的面积是 .
17.(4分)松松和东东骑自行车分别从迎宾大道上相距9500米的A、B两地同时出发,相向而行,行驶一段时间后松松的自行车坏了,立刻停车并马上打电话通知东东,东东接到电话后立刻提速至原来的倍,碰到松松后用了5分钟修好了松松的自行车,修好车后东东立刻骑车以提速后的速度继续向终点A地前行,松松则留在原地整理工具,2分钟以后松松以原速向B走了3分钟后,发现东东的包在自己身上,马上掉头以原速的倍的速度回A地;在整个行驶过程中,松松和东东均保持匀速行驶(东东停车和打电话的时间忽略不计),两人相距的路程S(米)与松松出发的时间t(分钟)之间的关系如图所示,则东东到达A地时,松松与A地的距离为 米.
18.(4分)甲、乙两辆小汽车在一个封闭的环形跑道内进行耐久测试.两车从同一地点沿相同方向同时起步后,乙车速超过甲车速,在第12分钟时甲车提速,在第15分钟时,甲车追上乙车并且开始超过乙,在第21分钟时,甲车再次追上乙车,已知在测试中甲、乙两车均是匀速行驶,那么如果甲车不提速,乙车首次超过甲车所用的时间是 分钟.
三、解答题:(本大题共2个小题,每小题8分,共16分)请把答案写在答题卡上对应的空白处,解答时每小题必须给出必要的演算过程或推理步骤。
19.(8分)如图,AB∥CD,点E在AB上,点F在CD上,连接EF,EH平分∠BEF,交CD于点H,过F作FG⊥EF,交EH于点G,若∠G=32°,求∠HFG的度数.
20.(8分)某市为提高环境质量对全市的环境污染进行综合治理,在治理的过程中环保部门随机选取了平安镇和富贵镇进行空气质量监测.
过程如下,请补充完整.
收集数据:
从2017年12月初开始连续一年对两镇的空气质量进行监测,将30天的空气污染指数(简称API)的平均值作为每个月的空气污染指数,12个月的空气污染指数如下:
平安镇:120 115 45 100 95 50 80 70 85 50 50 100
富贵镇:110 90 105 80 90 85 90 50 90 45 70 60
(1)整理、描述数据:
按下表整理、描述这两镇空气污染指数的数据:
空气质量为优
空气质量为良
空气质量为轻微污染
平安镇
4
6
2
富贵镇
(说明空气污染指数<50时,空气质量为优;50≤空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻度污染)
(2)分析数据:
两镇的空气污染指数的平均数、中位数、众数如表所示:
城镇
平均数
中位数
众数
平安镇
80
50
富贵镇
81.3
87.5
请将以上两个表格补充完整;
(3)得出结论:可以推断出 镇这一年中环境状况比较好,理由: .(至少从两个不同的角度说明推断的合理性)
四、解答题(本大题4个小题,每小题10分,共40分)解答时每小题都必须写出必要的演算过程或推理步骤,请将解答过程书写在答题卡中对应的位置上。
21.(10分)计算:
(1)(a+b)(a﹣b)﹣(a+b)2
(2)(+x﹣1)
22.(10分)如图,在平面直角坐标系中,直线l1与x轴交于点B,与y轴交于点C,直线l1与直线l2:y=x交于点A,将直线l2:y=x沿射线AB的方向平移得到直线l3,当l3经过点B时,与y轴交点记为D点,已知A点的纵坐标为﹣2,sin∠ABO=.
(1)求直线BC的解析式;
(2)求△ABD的面积.
23.(10分)某商店2月购进了甲乙两种货物共300千克,已知甲进价每千克20元,售价每千克40元,乙进价每千克5元,售价每千克10元.
(1)若这批货物全部销售完获利不低于4500元,则甲至少购进多少千克?
(2)第一批货物很快售完,于是商家决定购进第二批甲和乙两种货物,甲和乙的进价不变,经调查发现甲售价每上涨2元,销量比(1)中获得最低利润时的销量下降5千克:乙每千克售价比第一批上涨1.2元,销量与(1)中获得最低利润的销量保持不变,结果第二批中已经卖掉的甲和乙的销售总额比(1)中第一批甲和乙售完后对应的最低销售总额增加了480元,求第二批货物中甲的售价.
24.(10分)在平行四边形ABCD中,∠ABE=45°,点E在对角线AC上,BE的延长线交CD于点F,交AD的延长线于点G,过点C作CH⊥AB于点H,交BF于点M.
(1)若BE=3,AE=,求△ABE的面积;
(2)若∠ABC=3∠EBC.CA=CB,求证:CM=FG.
五、解答题(本大题2个小题,25题10分,26题12分,共22分)解答时每小题都必须写出必要的演算过程成推理步骤,请将解答过程书写在答题卡中对应的位置上。
25.(10分)我国著名的数学家秦九韶在《数书九章》提出了“三斜求积术”.即已知三角形的三边长,求它的面积.
用现代式子表示即为s=……①(其中a,b,c为三角形的三边长,s为面积.)
而另一个文明古国古希腊也有求三角形面积的海伦公式:
s=…②(其中a,b,c为三角形的三边长,p=)
(1)若已知三角形的三边长分别为5、7、8,请在上述两种公式中选择一种你喜欢的公式,计算该三角形的面积;
(2)事实上,“三斜求积术”与海伦公式是等价的,可以由“三斜求积术”直接推导出海伦公式,其部分推导过程如下:
∵[a2b2﹣()2]=[4a2b2﹣(a2+b2﹣c2)2]
=…
请将上述推导过程补充完整;
(3)如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1,以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x,试利用海伦公式求△ABC的最大面积.
26.(12分)二次函数y=﹣x2图象与x轴交于A、B两点,与y轴交于点C,连接AC、BC.
(1)如图1,求△ABC的周长;
(2)如图2,D为线段AB上一动点,作DE∥BC交AC于点E,当△CDE面积最大时,过E作x轴的平行线,交y轴于点F,交BC于点H,点P为线段FH上一动点,将△CFH绕点C沿逆时针方向旋转90°,点F,P,H的对应点分别是F′,P′,H′,点Q从点P出发,先沿适当的路径运动到点F′处,再沿F′C运动到点C处,最后沿适当的路径运动到点P′处停止,求点Q经过的最短路径的长是多少;
(3)如图3,点M是点C关于x轴的对称点,N是线段OB上一动点,经过MN的直线与抛物线交于点G,将△AMG沿MN翻折,点A的对应点是A′,是否存在点A′,使得△CBA′是等腰三角形,若存在求出点A′的坐标,若不存在,请说明理由.
2018-2019学年重庆外国语学校九年级(下)开学数学试卷
参考答案与试题解析
一、选择题(本大题共12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A,B,C,D的四个答案,其中只有一个是正确的,请将正确的答案的代号在答题卡中对应的方框涂黑。
1.【解答】解:∵﹣3.14<﹣2<0<,
∴四个实数0、、﹣3.14、﹣2中,最小的数是﹣3.14.
故选:C.
2.【解答】解:A.旋转180°,与原图形能够完全重合是中心对称图形;故此选项正确;
B.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项错误;
C.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项错误;
D.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项错误;
故选:A.
3.【解答】解:为了了解市民对电影《南京南京》的感受,小华在某校随机采访了8名初三学生不合适;
为了了解全校学生用于做数学作业的时间,小民同学在网上向3位好友做了调查不合适;
为了了解某段水域的水质情况,环保部门采用了抽样调查的方式,合适;
为了了解全市中学生每天的就寝时间,调查人员采用了普查的方式不合适;
故选:C.
4.【解答】解:设第n个图形有an个〇(n为正整数),
观察图形,可知:a1=1+3×1,a2=1+3×2,a3=1+3×3,a4=1+3×4,…,
∴an=1+3n(n为正整数),
∴a2019=1+3×2019=6058.
故选:D.
5.【解答】解:(A)∵DE∥BC,
∴△ADE∽△ABC,
∴,故A错误;
(B)∵DE∥BC,
∴,故B错误;
(C)∵DE∥BC,
,故C正确;
(D)∵DE∥BC,
∴△AGE∽△AFC,
∴=,故D错误;
故选:C.
6.【解答】解:①一组对边相等的四边形不一定是矩形,错误;
②两条对角线相等的平行四边形是矩形,错误;
③四条边都相等且对角线互相垂直的四边形是正方形,正确;
④四条边都相等的四边形是菱形,正确;
⑤一组邻边相等的矩形是正方形,正确.
故选:C.
7.【解答】解:∵9<11<16,
∴3<<4,即﹣4<﹣<﹣3,
∴18<22﹣<19,即18<(2﹣1)<19,
故选:C.
8.【解答】解:若4x+1=597,则有x=149,
若4x+1=149,则有x=37,
若4x+1=37,则有x=9,
若4x+1=9,则有x=2,
若4x+1=2,则有x=,
则满足条件的x不同值最多有5个,
故选:B.
9.【解答】解:∵AB是⊙O的切线,A为切点,
∴OA⊥AB,
∴∠OAB=90°,
∴OA===5,
∵OH⊥AC,
∴AH=CH,
在Rt△AOH中,AH==4.
∴AC=2AH=8.
故选:C.
10.【解答】解:如图
,
由斜坡轨道BC的坡度(或坡比)为i=1:2,得
BE:CE=1:2.
设BE=xm,CE=2xm.
在Rt△BCE中,由勾股定理,得
BE2+CE2=BC2,
即x2+(2x)2=(24)2,
解得x=24,
BE=24m,CE=48m,
DE=DC+CE=10+48=58m,
由tan36°≈0.73,得=0.73,
解得AB=0.73×58=42.34m.
由线段的和差,得
AB=AE﹣BE=42.34﹣24=18.34≈18.3m,
故选:B.
11.【解答】解:∵AD∥OE,AE∥OD,
∴四边形ADOE是平行四边形,
∴OD=AE,
又∵OD=CE,
∴AE=CE,
∴AC=2CE,
∴S矩形OCED=S△OAC,
∴S=|k|=,
又∵k>0,
∴k=5.
故选:D.
12.【解答】解:,
解不等式①得:x≤a,
解不等式②得:x>5,
∵关于x的不等式组无解,
∴a≤5.
①当二次函数y=(a﹣2)x2﹣2ax+a﹣与x轴有交点时,
方程(a﹣2)x2﹣2ax+a﹣=0的△=(﹣2a)2﹣4(a﹣2)(a﹣)≥0,
解得:a≥,
∴≤a≤5.
又∵a≠2,
整数有1,3,4,5,共4个.
②当函数y=(a﹣2)x2﹣2ax+a﹣是一次函数时,a﹣2=0,此时a=2.
综上所述,整数有1,2,3,4,5,共5个.
故选:C.
二、填空题:(本大题共6个小题,每小题4分,共24分)请把下列各题的正确答案填写在答题卡中对应的横线上.
13.【解答】解:+(﹣2018)0﹣4sin45°+|﹣2|
=2+1﹣4×+2
=2+1﹣2+2
=3.
故答案为:3.
14.【解答】解:2×2÷2﹣﹣=2﹣.
15.【解答】解:画树状图如下:
由树状图知共有12种等可能结果,
∵x2﹣5x+6=0的解为x=2或x=3,
∴数字m、n都不是方程x2﹣5x+6=0的解的有2种结果,
所以数字m、n都不是方程x2﹣5x+6=0的解的概率为=,
故答案为:.
16.【解答】解:根据AB:BC=4:5,设AB=4t,则有BC=5t,即A(5t,0),B(5t,4t),
∵E、D为反比例函数y=与BC、BA的交点,
∴D(5t,),E(,4t),
∵直线DE将△DBE翻折得△DFE,且点F恰好落在直线OA上,
∴BF⊥DE,BF的中点在DE上,
∵直线DE的斜率为=﹣,方程为y﹣4t=﹣(x﹣),
∴直线BF斜率为,
∴直线BF解析式为y﹣4t=(x﹣5t),即y=x﹣t,
令y=0,得到x=t,即F( t,0),
∴BF的中点坐标为( ,2t),
将中点坐标代入直线DE解析式得:2t﹣4t=﹣(﹣),
整理得:t2=,
则S矩形=5t?4t=20t2=.
故答案为:.
17.【解答】解:由题意:14分钟两人走了9500﹣1800=7700米(图中两人分别到了C,D)
∴两人的速度和为550米/分钟,
提速后东东的速度为800÷2=400米/分钟,
∴东东原来的速度=400÷=300米/分钟,
∴松松的速度为250米/分钟,
∴AC=250×14=3500米,BD=14×300=4200米,
设2分钟以后松松以原速向B走了3分钟到达点G,
∴修好车后东东到达A是时间为:=8.75分钟,此时松松到达点H,
∴东东到达A地时,松松与A地的距离HG=AC+CG﹣HG=3500+3×250﹣(8.75﹣2﹣3)×250×=2750米.
故答案为2750.
18.【解答】解:方法一:设甲车提速前速度比乙车慢a/分钟,提速后速度比乙车快b/分钟.
那么有甲车在第12分钟时,离乙车的距离为12a.这个距离在第15分钟追回来.
那么12a=(15﹣12)b.即b=4a,
而且在第21分钟时,甲车比乙车多跑一圈.
那么一圈的路程为(21﹣15)b=6b=24a,
所以甲车不提速时,乙车首次超过甲车(即多跑一圈)所需时间为:24a÷a=24分钟,
故答案为:24.
方法二:设甲车提速前的速度为x1,提速后的速度为x2,乙车的速度为y,
根据第12分钟时甲车提速,可得:3(x2﹣y)=12(y﹣x1),
化简得:(x2﹣y)=4(y﹣x1)①,
根据在第21分钟时,甲车再次追上乙车,可得:6(x2﹣y)=1,
化简,得:x2﹣y=②,
由①②可得:4(y﹣x1)=,
解得:y﹣x1=,
所以甲车不提速时,乙车首次超过甲车(即多跑一圈)所需时间为:=24.
故答案为:24.
三、解答题:(本大题共2个小题,每小题8分,共16分)请把答案写在答题卡上对应的空白处,解答时每小题必须给出必要的演算过程或推理步骤。
19.【解答】解:如图所示,∵FG⊥EF,∠G=32°,
∴∠GEF=58°,
∵EH平分∠BEF,
∴∠BEH=58°,
∵AB∥CD,
∴∠DHG=∠BEG=58°,
∴∠HFG=∠DHG﹣∠G=58°﹣32°=26°.
20.【解答】解:(1)富贵镇空气质量为优的天数是1天;空气质量为良的天数为9天;空气质量为轻微污染的天数为2天;
故答案为:1,9,2
(2)平安镇:120 115 100 100 95 85 80 70 50 50 50 45,
其中位于中间的两个数是85和80,所以其中位数为=82.5;
富贵镇的数据中,90出现了四次,出现的次数最多,故其众数为90.
故答案为82.5,90.
(3)平安镇的环境状况较好.
例如:平安镇空气质量优的天数多于富贵镇,平安镇的污染指数的平均数小于富贵镇或平安镇空气污染指数的众数是50,属于空气质量优,而富贵镇空气污染指数的众数是90,属于轻微污染等;
故答案为:平安镇;平安镇空气质量优的天数多于富贵镇,平安镇的污染指数的平均数小于富贵镇或平安镇空气污染指数的众数是50,属于空气质量优,而富贵镇空气污染指数的众数是90,属于轻微污染等.
四、解答题(本大题4个小题,每小题10分,共40分)解答时每小题都必须写出必要的演算过程或推理步骤,请将解答过程书写在答题卡中对应的位置上。
21.【解答】解:(1)(a+b)(a﹣b)﹣(a+b)2
=a2﹣b2﹣(a2+2ab+b2)
=﹣2b2﹣2ab;
(2)(+x﹣1)
=[+]×
=×
=×
=.
22.【解答】解:(1)∵点A的纵坐标为﹣2且在直线l2:y=x上
∴x=﹣2 解得:x=﹣4
∴A(﹣4,﹣2)
过A作AH⊥x轴于H,如图,则AH=2,OH=4
sin∠ABO==
∴AB=
∴BH===3
∴OB=OH+BH=7 即B(﹣7,0)
设直线BC解析式为y=kx+b,得:
解得:
∴直线BC解析式为y=﹣x﹣
(2)延长AH交BD于G,如图,
∵将直线l2:y=x平移得到直线l3
∴设直线l3:y=x+d,经过点B(﹣7,0)
解得d= 即D(0,),OD=
∵AG∥OD,AO∥DG
∴四边形AODG是平行四边形
∴AG=OD=
∴S△ABD=S△ABG+S△ADG
=AG?BH+AG?OH
=AG?OB
=
=
∴△ABD的面积为
23.【解答】解:(1)设购进甲x千克,则购进乙(300﹣x)千克,
根据题意得:(40﹣20)x+(10﹣5)(300﹣x)≥4500,
解得:x≥200.
答:甲至少购进200千克;
(2)设第二批货物中甲的售价为a,
根据题意得:a×[200﹣5(a﹣40)÷2]+(10+1.2)(300﹣200)=40×200+10×(300﹣200)+480,
整理得:a2﹣120a+1024=0,
解得:a1=44,a2=76(不合题意,舍去).
答:第二批货物中甲的售价为44.
24.【解答】解:(1)过E作EN⊥AB于N,
∵∠ABE=45°,
∴△BEN是等腰直角三角形,
∴BN=EN=BE=3,
∵AE=,
∴AN==1,
∴AB=4,
∴△ABE的面积=×4×3=6;
(2)∵∠ABE=45°,∠ABC=3∠EBC,
∴∠ABC=67.5°,
∵CA=CB,CH⊥AB,
∴∠CAB=∠CBA=67.5°,∠BCH=∠ACH=22.5°,
∴∠CME=∠BMH=∠MBH=45°,
∴∠CEM=112.5°,
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠FDG=∠BAD=112.5°,∠GFD=∠EBA=45°,
∴∠GFD=∠CME,∠FDG=∠MEC,
∵∠BCM=∠CBM=22.5°,
∴CM=BM,
∵∠BEA=∠EAB=67.5°,
∴BE=AB,
∴BE=CD,
在等腰直角三角形CMF中,
∵∠CMF=∠AFM=45°,
∴CM=CF,
∴BM=CF,
∴EM=DF,
在△MEC与△FDG中,,
∴△MEC≌△FDG(ASA),
∴CM=FG.
五、解答题(本大题2个小题,25题10分,26题12分,共22分)解答时每小题都必须写出必要的演算过程成推理步骤,请将解答过程书写在答题卡中对应的位置上。
25.【解答】(1)由题意,得 a=5,b=7,c=8,
∴p=,
∴△ABC面积=.
(2)∵s2=)]=
=
=p(p﹣a)(p﹣b)(p﹣c),
∴s=;
(3)由旋转性质得AC=MA=1,BC=BN=3﹣x,AB=x,p=2,
代入海伦公式,得△ABC的面积=,
∴当x=时,△ABC的面积最大,为.
26.【解答】解:(1)当x=0时,y=2,
∴C(0,2),
当y=0时,﹣x2=0,
解得:x=﹣或4,
∴A(﹣,0),B(4,0),
∴AB=5,
∵AC2==15,BC2==60,
∴△ABC的周长=AB+AC+BC=5++2=5+3;
(2)如图2,由(1)得:AC2+BC2=AB2,
∴∠ACB=90°,
∵DE∥BC,
∴∠AED=90°,
∵tan∠CAD====2,
设AE=m,ED=2m,AD=m,
∴CE=﹣m,
S△CED===﹣m2+m=﹣(m﹣)2+,
∴当m=时,即E是AC中点,△CDE面积最大,
连接OF',交EH于点P,连接CP,则CP=OP,
由旋转得:CP'=CP,
∴CP=OP=CP',
所以PF'+CF'+CP'=PF'+OP+CF'=OF'+CF'=+=+,
则点Q经过的最短路径的长是+;
(3)存在,分三种情况:
设A'(x,y),
①当A'C=A'B时,如图4,
∵A'C=A'B,AM=A'M,
∴,
解得:x=或(舍),
∴A'(,);
②当BC=CA'时,如图5,
∵AM=A'M,
∴,
解得:x=,y=﹣,
∴A'(,﹣);
③当BC=A'B时,如图6,
∵AM=A'M,
∴,
解得:x=或(舍),
A'(,),
综上,点A'的坐标为(,)或(,﹣)或(,).
同课章节目录
