2019年北师大版七下数学《第2章 相交线与平行线》单元测试卷(解析版)
文档属性
| 名称 | 2019年北师大版七下数学《第2章 相交线与平行线》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 302.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-22 18:40:26 | ||
图片预览



文档简介
2019年北师大版七下数学《第2章 相交线与平行线》单元测试卷
一.选择题(共10小题)
1.平面内有n条直线(n≥2),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b的值是( )
A.n(n﹣1) B.n2﹣n+1 C. D.
2.下面四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
3.如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为( )
A.75° B.15° C.105° D.165°
4.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点 B.B点 C.C点 D.D点
5.下列图形中线段PQ的长度表示点P到直线a的距离的是( )
A. B.
C. D.
6.如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
7.在同一个平面内,两条直线的位置关系是( )
A.平行或垂直 B.相交或垂直 C.平行或相交 D.不能确定
8.下列作图语句正确的是( )
A.延长线段AB到C,使AB=BC
B.延长射线AB
C.过点A作AB∥CD∥EF
D.作∠AOB的平分线OC
9.下列画图语句中,正确的是( )
A.画射线OP=3cm B.连接A,B两点
C.画出A,B两点的中点 D.画出A,B两点的距离
10.尺规作图的画图工具是( )
A.刻度尺、量角器 B.三角板、量角器
C.直尺、量角器 D.没有刻度的直尺和圆规
二.填空题(共5小题)
11.三条直线相交,最多有 个交点.
12.如图,∠1=15°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为 .
13.如图,直线AB.CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠AOC= 度.
14.如图所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由: .
15.如图,AB⊥l1,AC⊥l2,垂足分别为B,A,则A点到直线l1的距离是线段 的长度.
三.解答题(共6小题)
16.如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.
17.已知直线AB和CD相交于O点,CO⊥OE,OF平分∠AOE,∠COF=34°,求∠BOD的度数.
18.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
19.如图,点P是∠AOB的边OB上的一点,过点P画OB的垂线,交OA于点C;
(1)过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到 的距离, 是点C到直线OB的距离.线段PC、PH、OC这三条线段大小关系是 (用“<”号连接)
20.如图,∠1和∠2是哪两条直线被哪一条直线所截形成的?它们是什么角?∠1和∠3是哪两条直线被哪一条直线所截形成的?它们是什么角?
21.画图题:
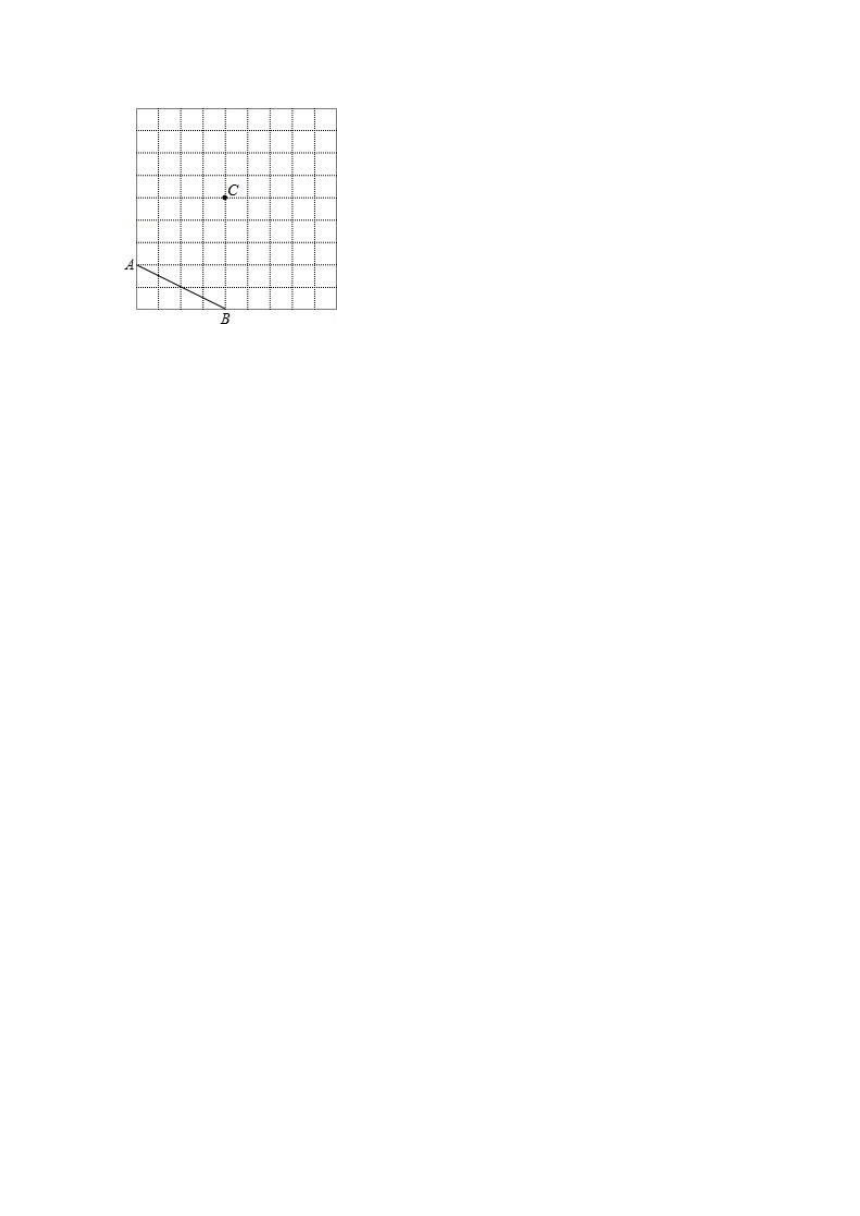
(1)在如图所示的方格纸中,经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线EF和平行线GH.
(2)判断EF、GH的位置关系是 .
(3)连接AC和BC,则三角形ABC的面积是 .
2019年北师大版七下数学《第2章 相交线与平行线》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.平面内有n条直线(n≥2),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b的值是( )
A.n(n﹣1) B.n2﹣n+1 C. D.
【分析】分别求出2条直线、3条直线、4条直线、5条直线…的交点个数,找出规律即可解答.
【解答】解:如图:2条直线相交有1个交点;
3条直线相交有1+2个交点;
4条直线相交有1+2+3个交点;
5条直线相交有1+2+3+4个交点;
6条直线相交有1+2+3+4+5个交点;
…
n条直线相交有1+2+3+4+5+…+(n﹣1)=个交点.
所以a=,而b=1,
∴a+b=.
故选D.
【点评】本题考查的是直线的交点问题,解答此题的关键是找出规律,需注意的是n条直线相交时最少有一个交点.
2.下面四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
【分析】根据对顶角的定义,可得答案.
【解答】解:由对顶角的定义,得C是对顶角,
故选:C.
【点评】本题考查了对顶角,对顶角中一个角的两边反向延长线是另一个角的两边.
3.如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为( )
A.75° B.15° C.105° D.165°
【分析】由图示可得,∠1与∠BOC互余,结合已知可求∠BOC,又因为∠2与∠COB互补,即可求出∠2.
【解答】解:∵∠1=15°,∠AOC=90°,
∴∠BOC=75°,
∵∠2+∠BOC=180°,
∴∠2=105°.
故选:C.
【点评】利用补角和余角的定义来计算,本题较简单.
4.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点 B.B点 C.C点 D.D点
【分析】根据垂线段最短可得答案.
【解答】解:根据垂线段最短可得:应建在A处,
故选:A.
【点评】此题主要考查了垂线段的性质,关键是掌握从直线外一点到这条直线所作的垂线段最短.
5.下列图形中线段PQ的长度表示点P到直线a的距离的是( )
A. B.
C. D.
【分析】根据点到直线的距离的定义,可得答案.
【解答】解:由题意得PQ⊥a,
P到a的距离是PQ垂线段的长,
故选:C.
【点评】本题考查了点到直线的距离,点到直线的距离是解题关键.
6.如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
【分析】根据同位角的定义,可得答案.
【解答】解:已知直线a、b被直线c所截,那么∠1的同位角是∠2,
故选:A.
【点评】本题考查了同位角,利用同为角的定义是解题关键.
7.在同一个平面内,两条直线的位置关系是( )
A.平行或垂直 B.相交或垂直 C.平行或相交 D.不能确定
【分析】在同一平面内不重合的两条直线,有两种位置关系:相交或平行,据此解答即可.
【解答】解:在同一个平面内的两条直线一定是平行或相交.
故选:C.
【点评】本题考查了同一平面两条直线的位置关系,解决本题的关键是在同一平面内不重合的两条直线,有两种位置关系:相交或平行.
8.下列作图语句正确的是( )
A.延长线段AB到C,使AB=BC
B.延长射线AB
C.过点A作AB∥CD∥EF
D.作∠AOB的平分线OC
【分析】根据基本作图的方法,逐项分析,从而得出正确的结论.
【解答】解:A、应为:延长线段AB到C,BC=AB,故本选项错误;
B、射线本身是无限延伸的,不能延长,故本选项错误;
C、过点A作只能作CD或EF的平行线,CD不一定平行于EF,故本选项错误;
D、作∠AOB的平分线OC,正确.
故选:D.
【点评】此题主要考查图形中延长线、平行线、角平分线的画法,是基本题型,特别是A选项,应该是作出的等于原来的,顺序不能颠倒.
9.下列画图语句中,正确的是( )
A.画射线OP=3cm B.连接A,B两点
C.画出A,B两点的中点 D.画出A,B两点的距离
【分析】根据基本作图的方法,逐项分析,从而得出正确的结论.
【解答】解:A、射线没有长度,错误;
B、连接A,B两点是作出线段AB,正确;
C、画出A,B两点的线段,量出中点,错误;
D、量出A,B两点的距离,错误.
故选:B.
【点评】本题考查常见的易错点,需在做题过程中加以熟练应用.
10.尺规作图的画图工具是( )
A.刻度尺、量角器 B.三角板、量角器
C.直尺、量角器 D.没有刻度的直尺和圆规
【分析】根据尺规作图的定义可知.
【解答】解:尺规作图的画图工具是没有刻度的直尺和圆规.
故选:D.
【点评】本题主要考查了尺规作图的画图工具,即没有刻度的直尺和圆规.
二.填空题(共5小题)
11.三条直线相交,最多有 3 个交点.
【分析】三条直线相交,有三种情况,即:两条直线平行,被第三条直线所截,有两个交点;三条直线经过同一个点,有一个交点;三条直线两两相交且不经过同一点,有三个交点.故可得答案.
【解答】解:三条直线相交时,位置关系如图所示:
判断可知:最多有3个交点.
【点评】解决本题的关键是画出三条直线相交时的三种情况,找出交点.
12.如图,∠1=15°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为 105° .
【分析】先求出∠BOC的度数,再根据邻补角的和等于180°列式进行计算即可求解.
【解答】解:∵∠1=15°,∠AOC=90°,
∴∠BOC=90°﹣15°=75°,
∴∠2=180°﹣∠BOC=180°﹣75°=105°.
故答案为:105°.
【点评】本题主要考查了邻补角的和等于180°的性质,比较简单,准确识图求出∠BOC的度数是解题的关键.
13.如图,直线AB.CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠AOC= 52 度.
【分析】根据垂线的定义,可得∠AOE=90°,根据角的和差,可得∠AOD的度数,根据邻补角的定义,可得答案.
【解答】解:∵OE⊥AB,
∴∠AOE=90°,
∴∠AOD=∠AOE+∠EOD=90°+38°=128°,
∴∠AOC=180°﹣∠AOD=180°﹣128°=52°,
故答案为:52.
【点评】本题考查了垂线的定义,对顶角相等,邻补角的和等于180°,要注意领会由垂直得直角这一要点.
14.如图所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由: 垂线段最短 .
【分析】根据从直线外一点到这条直线上各点所连的线段中,垂线段最短可知,要选垂线段.
【解答】解:为了使李庄人乘火车最方便(即距离最近),过李庄向铁路画垂线段,根据是垂线段最短.
故答案为:垂线段最短.
【点评】本题主要考查了从直线外一点到这条直线上各点所连的线段中,垂线段最短的性质.
15.如图,AB⊥l1,AC⊥l2,垂足分别为B,A,则A点到直线l1的距离是线段 AB 的长度.
【分析】根据点到直线的距离:直线外一点到直线的垂线段的长度,叫做点到直线的距离可得点P到直线l的距离是线段AB的长度.
【解答】解:∵AB⊥l1,
∴则A点到直线l1的距离是线段AB的长度,
故答案为:AB.
【点评】此题主要考查了点到直线的距离,点到直线的距离是一个长度,而不是一个图形,也就是垂线段的长度,而不是垂线段.
三.解答题(共6小题)
16.如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.
【分析】(1)根据对顶角相等求出∠BAOC的度数,设∠AOE=2x,根据题意列出方程,解方程即可;
(2)根据角平分线的定义求出∠BOF的度数即可.
【解答】解:(1)∵∠AOE:∠EOC=2:3.∴设∠AOE=2x,则∠EOC=3x,∴∠AOC=5x,
∵∠AOC=∠BOD=75°,
∴5x=75°,
解得:x=15°,
则2x=30°,
∴∠AOE=30°;
(2)OB是∠DOF的平分线;理由如下:
∵∠AOE=30°,
∴∠BOE=180°﹣∠AOE=150°,
∵OF平分∠BOE,
∴∠BOF=75°,
∵∠BOD=75°,
∴∠BOD=∠BOF,
∴OB是∠COF的角平分线.
【点评】本题考查的是对顶角、邻补角的概念和性质、角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.
17.已知直线AB和CD相交于O点,CO⊥OE,OF平分∠AOE,∠COF=34°,求∠BOD的度数.
【分析】根据垂直的定义、角平分线线的定义以及图中的角与角间的和差关系得到∠AOF=∠EOF=∠COE﹣∠COF=90°﹣34°=56°,则对顶角∠BOD=∠AOC=22°.
【解答】解:∵CO⊥OE,
∴∠COE=90°,
∵∠COF=34°
∴∠EOF=90°﹣34°=56°
又∵OF平分∠AOE
∴∠AOF=∠EOF=56°
∵∠COF=34°
∴∠AOC=56°﹣34°=22°
则∠BOD=∠AOC=22°.
【点评】此题主要考查了角平分线的定义,根据角平分线定义得出所求角与已知角的关系转化求解.
18.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
【分析】(1)从火车站到码头的距离是点到点的距离,即两点间的距离.依据两点之间线段最短解答.
(2)从码头到铁路的距离是点到直线的距离.依据垂线段最短解答.
(3)从火车站到河流的距离是点到直线的距离.依据垂线段最短解答.
【解答】解:如图所示
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
【点评】根据具体的问题正确判断出是点到点的距离还是点到线的距离是解答问题的关键.
19.如图,点P是∠AOB的边OB上的一点,过点P画OB的垂线,交OA于点C;
(1)过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到 OA 的距离, 线段CP的长度 是点C到直线OB的距离.线段PC、PH、OC这三条线段大小关系是 PH<PC<OC (用“<”号连接)
【分析】(1)过点P画OA的垂线,即过点P画∠PHO=90°即可,
(2)利用点到直线的距离可以判断线段PH的长度是点P到OA的距离,PC是点C到直线OB的距离,线段PC、PH、OC这三条线段大小关系是PH<PC<OC.
【解答】解:(1)如图:
(2)线段PH的长度是点P到直线OA的距离,
线段CP的长度是点C到直线OB的距离,
根据垂线段最短可得:PH<PC<OC,
故答案为:OA,线段CP,PH<PC<OC.
【点评】本题主要考查了基本作图﹣﹣﹣﹣作已知直线的垂线,另外还需利用点到直线的距离才可解决问题.
20.如图,∠1和∠2是哪两条直线被哪一条直线所截形成的?它们是什么角?∠1和∠3是哪两条直线被哪一条直线所截形成的?它们是什么角?
【分析】根据同位角的概念作答.准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.
【解答】解:∠1和∠2是直线EF、DC被直线AB所截形成的同位角,∠1和∠3是直线AB、CD被直线EF所截形成的同位角.
【点评】同位角,即位置相同,两个角都在第三条直线的同旁,同在被截两条直线的上方或下方.在截线的同旁找同位角和同旁内角,在截线的两旁找内错角.要结合图形,熟记同位角、内错角、同旁内角的位置特点,比较它们的区别与联系.
21.画图题:
(1)在如图所示的方格纸中,经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线EF和平行线GH.
(2)判断EF、GH的位置关系是 垂直 .
(3)连接AC和BC,则三角形ABC的面积是 10 .
【分析】(1)过点C作5×1的矩形的对角线所在的直线,可得AB的垂线和平行线;
(2)易得EF与GH的位置关系是:垂直;
(3)根据三角形的面积公式解答.
【解答】解:(1)如图
(2)EF与GH的位置关系是:垂直;
(3)设小方格的边长是1,则
AB=2,CH=2,
∴S△ABC=×2×2=10.
【点评】此题灵活考查了过直线外一点作它的平行线、垂线,以及学生的观察、总结能力.
一.选择题(共10小题)
1.平面内有n条直线(n≥2),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b的值是( )
A.n(n﹣1) B.n2﹣n+1 C. D.
2.下面四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
3.如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为( )
A.75° B.15° C.105° D.165°
4.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点 B.B点 C.C点 D.D点
5.下列图形中线段PQ的长度表示点P到直线a的距离的是( )
A. B.
C. D.
6.如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
7.在同一个平面内,两条直线的位置关系是( )
A.平行或垂直 B.相交或垂直 C.平行或相交 D.不能确定
8.下列作图语句正确的是( )
A.延长线段AB到C,使AB=BC
B.延长射线AB
C.过点A作AB∥CD∥EF
D.作∠AOB的平分线OC
9.下列画图语句中,正确的是( )
A.画射线OP=3cm B.连接A,B两点
C.画出A,B两点的中点 D.画出A,B两点的距离
10.尺规作图的画图工具是( )
A.刻度尺、量角器 B.三角板、量角器
C.直尺、量角器 D.没有刻度的直尺和圆规
二.填空题(共5小题)
11.三条直线相交,最多有 个交点.
12.如图,∠1=15°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为 .
13.如图,直线AB.CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠AOC= 度.
14.如图所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由: .
15.如图,AB⊥l1,AC⊥l2,垂足分别为B,A,则A点到直线l1的距离是线段 的长度.
三.解答题(共6小题)
16.如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.
17.已知直线AB和CD相交于O点,CO⊥OE,OF平分∠AOE,∠COF=34°,求∠BOD的度数.
18.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
19.如图,点P是∠AOB的边OB上的一点,过点P画OB的垂线,交OA于点C;
(1)过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到 的距离, 是点C到直线OB的距离.线段PC、PH、OC这三条线段大小关系是 (用“<”号连接)
20.如图,∠1和∠2是哪两条直线被哪一条直线所截形成的?它们是什么角?∠1和∠3是哪两条直线被哪一条直线所截形成的?它们是什么角?
21.画图题:
(1)在如图所示的方格纸中,经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线EF和平行线GH.
(2)判断EF、GH的位置关系是 .
(3)连接AC和BC,则三角形ABC的面积是 .
2019年北师大版七下数学《第2章 相交线与平行线》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.平面内有n条直线(n≥2),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b的值是( )
A.n(n﹣1) B.n2﹣n+1 C. D.
【分析】分别求出2条直线、3条直线、4条直线、5条直线…的交点个数,找出规律即可解答.
【解答】解:如图:2条直线相交有1个交点;
3条直线相交有1+2个交点;
4条直线相交有1+2+3个交点;
5条直线相交有1+2+3+4个交点;
6条直线相交有1+2+3+4+5个交点;
…
n条直线相交有1+2+3+4+5+…+(n﹣1)=个交点.
所以a=,而b=1,
∴a+b=.
故选D.
【点评】本题考查的是直线的交点问题,解答此题的关键是找出规律,需注意的是n条直线相交时最少有一个交点.
2.下面四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
【分析】根据对顶角的定义,可得答案.
【解答】解:由对顶角的定义,得C是对顶角,
故选:C.
【点评】本题考查了对顶角,对顶角中一个角的两边反向延长线是另一个角的两边.
3.如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为( )
A.75° B.15° C.105° D.165°
【分析】由图示可得,∠1与∠BOC互余,结合已知可求∠BOC,又因为∠2与∠COB互补,即可求出∠2.
【解答】解:∵∠1=15°,∠AOC=90°,
∴∠BOC=75°,
∵∠2+∠BOC=180°,
∴∠2=105°.
故选:C.
【点评】利用补角和余角的定义来计算,本题较简单.
4.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点 B.B点 C.C点 D.D点
【分析】根据垂线段最短可得答案.
【解答】解:根据垂线段最短可得:应建在A处,
故选:A.
【点评】此题主要考查了垂线段的性质,关键是掌握从直线外一点到这条直线所作的垂线段最短.
5.下列图形中线段PQ的长度表示点P到直线a的距离的是( )
A. B.
C. D.
【分析】根据点到直线的距离的定义,可得答案.
【解答】解:由题意得PQ⊥a,
P到a的距离是PQ垂线段的长,
故选:C.
【点评】本题考查了点到直线的距离,点到直线的距离是解题关键.
6.如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
【分析】根据同位角的定义,可得答案.
【解答】解:已知直线a、b被直线c所截,那么∠1的同位角是∠2,
故选:A.
【点评】本题考查了同位角,利用同为角的定义是解题关键.
7.在同一个平面内,两条直线的位置关系是( )
A.平行或垂直 B.相交或垂直 C.平行或相交 D.不能确定
【分析】在同一平面内不重合的两条直线,有两种位置关系:相交或平行,据此解答即可.
【解答】解:在同一个平面内的两条直线一定是平行或相交.
故选:C.
【点评】本题考查了同一平面两条直线的位置关系,解决本题的关键是在同一平面内不重合的两条直线,有两种位置关系:相交或平行.
8.下列作图语句正确的是( )
A.延长线段AB到C,使AB=BC
B.延长射线AB
C.过点A作AB∥CD∥EF
D.作∠AOB的平分线OC
【分析】根据基本作图的方法,逐项分析,从而得出正确的结论.
【解答】解:A、应为:延长线段AB到C,BC=AB,故本选项错误;
B、射线本身是无限延伸的,不能延长,故本选项错误;
C、过点A作只能作CD或EF的平行线,CD不一定平行于EF,故本选项错误;
D、作∠AOB的平分线OC,正确.
故选:D.
【点评】此题主要考查图形中延长线、平行线、角平分线的画法,是基本题型,特别是A选项,应该是作出的等于原来的,顺序不能颠倒.
9.下列画图语句中,正确的是( )
A.画射线OP=3cm B.连接A,B两点
C.画出A,B两点的中点 D.画出A,B两点的距离
【分析】根据基本作图的方法,逐项分析,从而得出正确的结论.
【解答】解:A、射线没有长度,错误;
B、连接A,B两点是作出线段AB,正确;
C、画出A,B两点的线段,量出中点,错误;
D、量出A,B两点的距离,错误.
故选:B.
【点评】本题考查常见的易错点,需在做题过程中加以熟练应用.
10.尺规作图的画图工具是( )
A.刻度尺、量角器 B.三角板、量角器
C.直尺、量角器 D.没有刻度的直尺和圆规
【分析】根据尺规作图的定义可知.
【解答】解:尺规作图的画图工具是没有刻度的直尺和圆规.
故选:D.
【点评】本题主要考查了尺规作图的画图工具,即没有刻度的直尺和圆规.
二.填空题(共5小题)
11.三条直线相交,最多有 3 个交点.
【分析】三条直线相交,有三种情况,即:两条直线平行,被第三条直线所截,有两个交点;三条直线经过同一个点,有一个交点;三条直线两两相交且不经过同一点,有三个交点.故可得答案.
【解答】解:三条直线相交时,位置关系如图所示:
判断可知:最多有3个交点.
【点评】解决本题的关键是画出三条直线相交时的三种情况,找出交点.
12.如图,∠1=15°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为 105° .
【分析】先求出∠BOC的度数,再根据邻补角的和等于180°列式进行计算即可求解.
【解答】解:∵∠1=15°,∠AOC=90°,
∴∠BOC=90°﹣15°=75°,
∴∠2=180°﹣∠BOC=180°﹣75°=105°.
故答案为:105°.
【点评】本题主要考查了邻补角的和等于180°的性质,比较简单,准确识图求出∠BOC的度数是解题的关键.
13.如图,直线AB.CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠AOC= 52 度.
【分析】根据垂线的定义,可得∠AOE=90°,根据角的和差,可得∠AOD的度数,根据邻补角的定义,可得答案.
【解答】解:∵OE⊥AB,
∴∠AOE=90°,
∴∠AOD=∠AOE+∠EOD=90°+38°=128°,
∴∠AOC=180°﹣∠AOD=180°﹣128°=52°,
故答案为:52.
【点评】本题考查了垂线的定义,对顶角相等,邻补角的和等于180°,要注意领会由垂直得直角这一要点.
14.如图所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由: 垂线段最短 .
【分析】根据从直线外一点到这条直线上各点所连的线段中,垂线段最短可知,要选垂线段.
【解答】解:为了使李庄人乘火车最方便(即距离最近),过李庄向铁路画垂线段,根据是垂线段最短.
故答案为:垂线段最短.
【点评】本题主要考查了从直线外一点到这条直线上各点所连的线段中,垂线段最短的性质.
15.如图,AB⊥l1,AC⊥l2,垂足分别为B,A,则A点到直线l1的距离是线段 AB 的长度.
【分析】根据点到直线的距离:直线外一点到直线的垂线段的长度,叫做点到直线的距离可得点P到直线l的距离是线段AB的长度.
【解答】解:∵AB⊥l1,
∴则A点到直线l1的距离是线段AB的长度,
故答案为:AB.
【点评】此题主要考查了点到直线的距离,点到直线的距离是一个长度,而不是一个图形,也就是垂线段的长度,而不是垂线段.
三.解答题(共6小题)
16.如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.
【分析】(1)根据对顶角相等求出∠BAOC的度数,设∠AOE=2x,根据题意列出方程,解方程即可;
(2)根据角平分线的定义求出∠BOF的度数即可.
【解答】解:(1)∵∠AOE:∠EOC=2:3.∴设∠AOE=2x,则∠EOC=3x,∴∠AOC=5x,
∵∠AOC=∠BOD=75°,
∴5x=75°,
解得:x=15°,
则2x=30°,
∴∠AOE=30°;
(2)OB是∠DOF的平分线;理由如下:
∵∠AOE=30°,
∴∠BOE=180°﹣∠AOE=150°,
∵OF平分∠BOE,
∴∠BOF=75°,
∵∠BOD=75°,
∴∠BOD=∠BOF,
∴OB是∠COF的角平分线.
【点评】本题考查的是对顶角、邻补角的概念和性质、角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.
17.已知直线AB和CD相交于O点,CO⊥OE,OF平分∠AOE,∠COF=34°,求∠BOD的度数.
【分析】根据垂直的定义、角平分线线的定义以及图中的角与角间的和差关系得到∠AOF=∠EOF=∠COE﹣∠COF=90°﹣34°=56°,则对顶角∠BOD=∠AOC=22°.
【解答】解:∵CO⊥OE,
∴∠COE=90°,
∵∠COF=34°
∴∠EOF=90°﹣34°=56°
又∵OF平分∠AOE
∴∠AOF=∠EOF=56°
∵∠COF=34°
∴∠AOC=56°﹣34°=22°
则∠BOD=∠AOC=22°.
【点评】此题主要考查了角平分线的定义,根据角平分线定义得出所求角与已知角的关系转化求解.
18.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
【分析】(1)从火车站到码头的距离是点到点的距离,即两点间的距离.依据两点之间线段最短解答.
(2)从码头到铁路的距离是点到直线的距离.依据垂线段最短解答.
(3)从火车站到河流的距离是点到直线的距离.依据垂线段最短解答.
【解答】解:如图所示
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
【点评】根据具体的问题正确判断出是点到点的距离还是点到线的距离是解答问题的关键.
19.如图,点P是∠AOB的边OB上的一点,过点P画OB的垂线,交OA于点C;
(1)过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到 OA 的距离, 线段CP的长度 是点C到直线OB的距离.线段PC、PH、OC这三条线段大小关系是 PH<PC<OC (用“<”号连接)
【分析】(1)过点P画OA的垂线,即过点P画∠PHO=90°即可,
(2)利用点到直线的距离可以判断线段PH的长度是点P到OA的距离,PC是点C到直线OB的距离,线段PC、PH、OC这三条线段大小关系是PH<PC<OC.
【解答】解:(1)如图:
(2)线段PH的长度是点P到直线OA的距离,
线段CP的长度是点C到直线OB的距离,
根据垂线段最短可得:PH<PC<OC,
故答案为:OA,线段CP,PH<PC<OC.
【点评】本题主要考查了基本作图﹣﹣﹣﹣作已知直线的垂线,另外还需利用点到直线的距离才可解决问题.
20.如图,∠1和∠2是哪两条直线被哪一条直线所截形成的?它们是什么角?∠1和∠3是哪两条直线被哪一条直线所截形成的?它们是什么角?
【分析】根据同位角的概念作答.准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.
【解答】解:∠1和∠2是直线EF、DC被直线AB所截形成的同位角,∠1和∠3是直线AB、CD被直线EF所截形成的同位角.
【点评】同位角,即位置相同,两个角都在第三条直线的同旁,同在被截两条直线的上方或下方.在截线的同旁找同位角和同旁内角,在截线的两旁找内错角.要结合图形,熟记同位角、内错角、同旁内角的位置特点,比较它们的区别与联系.
21.画图题:
(1)在如图所示的方格纸中,经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线EF和平行线GH.
(2)判断EF、GH的位置关系是 垂直 .
(3)连接AC和BC,则三角形ABC的面积是 10 .
【分析】(1)过点C作5×1的矩形的对角线所在的直线,可得AB的垂线和平行线;
(2)易得EF与GH的位置关系是:垂直;
(3)根据三角形的面积公式解答.
【解答】解:(1)如图
(2)EF与GH的位置关系是:垂直;
(3)设小方格的边长是1,则
AB=2,CH=2,
∴S△ABC=×2×2=10.
【点评】此题灵活考查了过直线外一点作它的平行线、垂线,以及学生的观察、总结能力.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
