北师大版 高中数学 必修三 3.2.1古典概型的特征和概率计算公式(24ppt)
文档属性
| 名称 | 北师大版 高中数学 必修三 3.2.1古典概型的特征和概率计算公式(24ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-23 00:00:00 | ||
图片预览







文档简介
§2 古典概型
2.1 古典概型的特征和概率计算公式
1、通过实例对古典概型概念的归纳和总结,使学生体 验知识产生和形成的过程,培养学生的抽象概括能力.
2、理解古典概型的概念,通过实例归纳出古典概型概率计算公式,能运用公式求一些简单的古典概型的概率.
学习重点:
知道基本事件特征并理解古典概型的概念及利用古典概型求解随机事件的概率.
学习难点:
基本事件特征及如何判断一个试验是否为古典概型,弄清在一个古典概型中某随机事件所包含的基本事件的个数和试验中基本事件的总数.
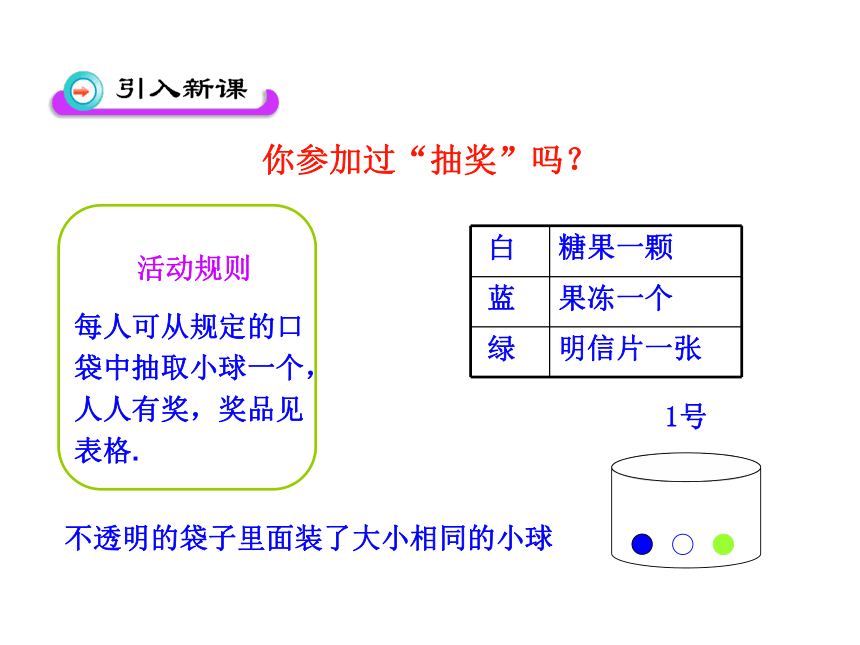
你参加过“抽奖”吗?
不透明的袋子里面装了大小相同的小球
白 糖果一颗
蓝 果冻一个
绿 明信片一张
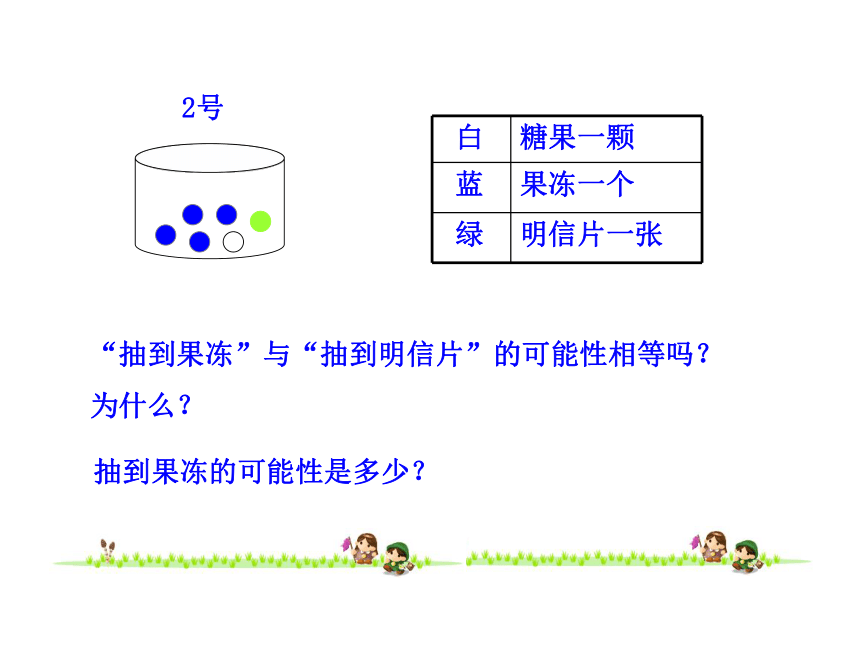
“抽到果冻”与“抽到明信片”的可能性相等吗?为什么?
抽到果冻的可能性是多少?
白 糖果一颗
蓝 果冻一个
绿 明信片一张
掷硬币实验
摇骰子实验
转盘实验
试验一:抛掷一枚均匀的硬币,试验的结果有__个,
其中出现“正面朝上”的概率=___.出现“反面朝
上”的概率=___.
试验二:掷一粒均匀的骰子,试验结果有___
个,其中出现“点数5”的概率=___.
试验三:转8等分标记的转盘,试验结果有___个,
出现“箭头指向4”的概率=___.
上述三个试验有什么特点?
归纳上述三个试验的特点:
1、试验的所有可能结果只有有限个,每次试验只出现其中的一个结果.
2、每一个试验结果出现的可能性相同.
我们把具有这样两个特征的随机试验的数学模型称为古典概型(等可能事件).
.............
.............
1、向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,你认为这是古典概型吗?为什么?
〖解〗因为试验的所有可能结果是圆面内所有的点,试验的所有可能结果数是无限的,虽然每一个试验结果出现的“可能性相同”,但这个试验不满足古典概型的第一个条件.
.............
.............
.............
2、如图,射击运动员向一靶心进行射击,这一试验的结果只有有限个:命中10环、命中9环……命中1环和命中0环.你认为这是古典概型吗?为什么?
〖解〗不是古典概型,因为试验的所有可能结果只有11个,而命中10环、命中9环……命中1环和不中环的出现不是等可能的,即不满足古典概型的第二个条件.
掷一粒均匀的骰子,骰子落地时向上的点数为2的概率是多少?点数为4的概率呢?点数为6的概率呢?骰子落地时向上的点数为偶数的概率是多少?
分析:用事件A表示“向上的点数为偶数”,则事件A由“点数为2”、“点数为4”、“点数为6”三个可能结果组成,又出现“点数为2”的概率为 ,出现“点数为4”的概率为 ,出现“点数为6”的概率为 ,
且A的发生,指三种情形之一的出现,因此
即骰子落地时向上的点数为偶数的概率是 .
思考二:
古典概型中,试验的所有可能结果(基本事件)数为n,随机事件A包含m个基本事件,那么随机事件A的概率规定为:
应该注意:
(1)要判断该概率模型是不是古典概型;
(2)要找出随机事件A包含的基本事件的个数和
试验中基本事件的总数.
如图,转动转盘计算下列事件的概率:
(1)箭头指向8;
(2)箭头指向3或8;
(3)箭头不指向8;
(4)箭头指向偶数;
例1 在一个健身房里,用拉力器进行锻炼时,需要选取2
个质量盘装在拉力器上.有2个装质量盘的箱子,每个箱子
中都装有4个不同的质量盘:2.5 kg、5 kg、10 kg和
20 kg,每次都随机地从2个箱子中各取1个质量盘装在拉
力器上后,再拉动这个拉力器.
(1)随机地从2个箱子中各取1个质量盘,共有多少种可能
的结果?用表格列出所有可能的结果.
(2)计算选取的两个质量盘的总质量分别是下列质量的概
率.
(ⅰ)20 kg;(ⅱ)30 kg;
(ⅲ)不超过10 kg;(ⅳ)超过10 kg.
(3)如果一个人不能拉动超过22 kg的质量,那么他不能
拉开拉力器的概率是多少?
解:(1)第一个箱子的质量盘和第二个箱子的质量盘都可以
从4种不同的质量盘中任意选取.我们可以用一个“有序实数
对”来表示随机选取的结果.例如,我们用(10,20)来表
示:在一次随机的选取中,从第一个箱子取的质量盘是10 kg,
从第二个箱子取的质量盘是20 kg,表1列出了所有可
能的结果.
表1
第二质量
第一质量 2.5 5 10 20
2.5 (2.5,2.5) (2.5,5) (2.5,10) (2.5,20)
5 (5,2.5) (5,5) (5,10) (5,20)
10 (10,2.5) (10,5) (10,10) (10,20)
20 (20,2.5) (20,5) (20,10) (20,20)
从上表中可以看出,随机地从2个箱子中各取1个质量盘的
所有可能结果数有16种.由于选取质量盘是随机的,因此
这16种结果出现的可能性是相同的,这个试验属于古典概
型.
(2)表2
(ⅰ)用A表示事件“选取的两个质量盘的总质量是
20 kg”,因为总质量为20 kg的所有可能结果只有1种,
因此,事件A的概率P(A)= =0.062 5.
(ⅱ)用B表示事件“选取的两个质量盘的总质量是
30 kg”,从表2中可以看出,总质量为30 kg的所有可
能结果共有2种,因此事件B的概率
P(B)= = =0.125.
(ⅲ)用C表示事件“选取的两个质量盘的总质量不超过
10 kg”,总质量不超过10 kg,即总质量为5 kg,7.5 kg,
10 kg,从表2中容易看出,所有可能结果共有4种,因
此,事件C的概率
P(C)= = =0.25.
(ⅳ)用D表示事件“选取的两个质量盘的总质量超过
10 kg”,总质量超过10 kg,即总质量为12.5 kg,20 kg,
15 kg,22.5 kg,25 kg,30 kg,40 kg,从表2中可以看出,
所有可能结果共有12种,因此,事件D的概率
P(D)= = =0.75.
(3)用E表示事件“不能拉开拉力器”,即总质量超过了
22 kg,总质量超过22 kg是指总质量为22.5 kg,25 kg,
30 kg,40 kg,从表2中可以看出,这样的可能结果
共有7种,因此,不能拉开拉力器的概率
P(E)= ≈0.44.
规律方法:
在这个例子中,用列表的方法列出了所有可能的结果.在计算古典概率时,只要所有可能结果的数量不是很多,列举法是我们常用的一种方法.
单选题是标准化考试中常用的题型,一般是从A,B,C,D四个选项中选择一个正确答案.如果考生掌握了考察的内容,他可以选择唯一正确的答案.假设考生不会做,他随机的选择一个答案,问他答对的概率是多少?
解:这是一个古典概型,因为试验的可能结果只有4个:选择A、选择B、选择C、选择D,即基本事件共有4个,考生随机地选择一个答案即选择A,B,C,D的可能性是相等的.从而由古典概型的概率计算公式得:
1.古典概型:
我们将具有:
(1)试验中所有可能出现的基本事件只有有限个;(有限性)
(2)每个基本事件出现的可能性相等.(等可能性)
这样两个特点的概率模型称为古典概率概型,简称古典概型.
2.古典概型计算任何事件的概率计算公式为:
3.求某个随机事件A包含的基本事件的个数和实验中基本事件的总数时常用的方法是列举法(画树状图和列表),注意做到不重不漏.
自小多才学,平生志气高;
别人怀宝剑,我有笔和刀 .
-------《神童诗》
2.1 古典概型的特征和概率计算公式
1、通过实例对古典概型概念的归纳和总结,使学生体 验知识产生和形成的过程,培养学生的抽象概括能力.
2、理解古典概型的概念,通过实例归纳出古典概型概率计算公式,能运用公式求一些简单的古典概型的概率.
学习重点:
知道基本事件特征并理解古典概型的概念及利用古典概型求解随机事件的概率.
学习难点:
基本事件特征及如何判断一个试验是否为古典概型,弄清在一个古典概型中某随机事件所包含的基本事件的个数和试验中基本事件的总数.
你参加过“抽奖”吗?
不透明的袋子里面装了大小相同的小球
白 糖果一颗
蓝 果冻一个
绿 明信片一张
“抽到果冻”与“抽到明信片”的可能性相等吗?为什么?
抽到果冻的可能性是多少?
白 糖果一颗
蓝 果冻一个
绿 明信片一张
掷硬币实验
摇骰子实验
转盘实验
试验一:抛掷一枚均匀的硬币,试验的结果有__个,
其中出现“正面朝上”的概率=___.出现“反面朝
上”的概率=___.
试验二:掷一粒均匀的骰子,试验结果有___
个,其中出现“点数5”的概率=___.
试验三:转8等分标记的转盘,试验结果有___个,
出现“箭头指向4”的概率=___.
上述三个试验有什么特点?
归纳上述三个试验的特点:
1、试验的所有可能结果只有有限个,每次试验只出现其中的一个结果.
2、每一个试验结果出现的可能性相同.
我们把具有这样两个特征的随机试验的数学模型称为古典概型(等可能事件).
.............
.............
1、向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,你认为这是古典概型吗?为什么?
〖解〗因为试验的所有可能结果是圆面内所有的点,试验的所有可能结果数是无限的,虽然每一个试验结果出现的“可能性相同”,但这个试验不满足古典概型的第一个条件.
.............
.............
.............
2、如图,射击运动员向一靶心进行射击,这一试验的结果只有有限个:命中10环、命中9环……命中1环和命中0环.你认为这是古典概型吗?为什么?
〖解〗不是古典概型,因为试验的所有可能结果只有11个,而命中10环、命中9环……命中1环和不中环的出现不是等可能的,即不满足古典概型的第二个条件.
掷一粒均匀的骰子,骰子落地时向上的点数为2的概率是多少?点数为4的概率呢?点数为6的概率呢?骰子落地时向上的点数为偶数的概率是多少?
分析:用事件A表示“向上的点数为偶数”,则事件A由“点数为2”、“点数为4”、“点数为6”三个可能结果组成,又出现“点数为2”的概率为 ,出现“点数为4”的概率为 ,出现“点数为6”的概率为 ,
且A的发生,指三种情形之一的出现,因此
即骰子落地时向上的点数为偶数的概率是 .
思考二:
古典概型中,试验的所有可能结果(基本事件)数为n,随机事件A包含m个基本事件,那么随机事件A的概率规定为:
应该注意:
(1)要判断该概率模型是不是古典概型;
(2)要找出随机事件A包含的基本事件的个数和
试验中基本事件的总数.
如图,转动转盘计算下列事件的概率:
(1)箭头指向8;
(2)箭头指向3或8;
(3)箭头不指向8;
(4)箭头指向偶数;
例1 在一个健身房里,用拉力器进行锻炼时,需要选取2
个质量盘装在拉力器上.有2个装质量盘的箱子,每个箱子
中都装有4个不同的质量盘:2.5 kg、5 kg、10 kg和
20 kg,每次都随机地从2个箱子中各取1个质量盘装在拉
力器上后,再拉动这个拉力器.
(1)随机地从2个箱子中各取1个质量盘,共有多少种可能
的结果?用表格列出所有可能的结果.
(2)计算选取的两个质量盘的总质量分别是下列质量的概
率.
(ⅰ)20 kg;(ⅱ)30 kg;
(ⅲ)不超过10 kg;(ⅳ)超过10 kg.
(3)如果一个人不能拉动超过22 kg的质量,那么他不能
拉开拉力器的概率是多少?
解:(1)第一个箱子的质量盘和第二个箱子的质量盘都可以
从4种不同的质量盘中任意选取.我们可以用一个“有序实数
对”来表示随机选取的结果.例如,我们用(10,20)来表
示:在一次随机的选取中,从第一个箱子取的质量盘是10 kg,
从第二个箱子取的质量盘是20 kg,表1列出了所有可
能的结果.
表1
第二质量
第一质量 2.5 5 10 20
2.5 (2.5,2.5) (2.5,5) (2.5,10) (2.5,20)
5 (5,2.5) (5,5) (5,10) (5,20)
10 (10,2.5) (10,5) (10,10) (10,20)
20 (20,2.5) (20,5) (20,10) (20,20)
从上表中可以看出,随机地从2个箱子中各取1个质量盘的
所有可能结果数有16种.由于选取质量盘是随机的,因此
这16种结果出现的可能性是相同的,这个试验属于古典概
型.
(2)表2
(ⅰ)用A表示事件“选取的两个质量盘的总质量是
20 kg”,因为总质量为20 kg的所有可能结果只有1种,
因此,事件A的概率P(A)= =0.062 5.
(ⅱ)用B表示事件“选取的两个质量盘的总质量是
30 kg”,从表2中可以看出,总质量为30 kg的所有可
能结果共有2种,因此事件B的概率
P(B)= = =0.125.
(ⅲ)用C表示事件“选取的两个质量盘的总质量不超过
10 kg”,总质量不超过10 kg,即总质量为5 kg,7.5 kg,
10 kg,从表2中容易看出,所有可能结果共有4种,因
此,事件C的概率
P(C)= = =0.25.
(ⅳ)用D表示事件“选取的两个质量盘的总质量超过
10 kg”,总质量超过10 kg,即总质量为12.5 kg,20 kg,
15 kg,22.5 kg,25 kg,30 kg,40 kg,从表2中可以看出,
所有可能结果共有12种,因此,事件D的概率
P(D)= = =0.75.
(3)用E表示事件“不能拉开拉力器”,即总质量超过了
22 kg,总质量超过22 kg是指总质量为22.5 kg,25 kg,
30 kg,40 kg,从表2中可以看出,这样的可能结果
共有7种,因此,不能拉开拉力器的概率
P(E)= ≈0.44.
规律方法:
在这个例子中,用列表的方法列出了所有可能的结果.在计算古典概率时,只要所有可能结果的数量不是很多,列举法是我们常用的一种方法.
单选题是标准化考试中常用的题型,一般是从A,B,C,D四个选项中选择一个正确答案.如果考生掌握了考察的内容,他可以选择唯一正确的答案.假设考生不会做,他随机的选择一个答案,问他答对的概率是多少?
解:这是一个古典概型,因为试验的可能结果只有4个:选择A、选择B、选择C、选择D,即基本事件共有4个,考生随机地选择一个答案即选择A,B,C,D的可能性是相等的.从而由古典概型的概率计算公式得:
1.古典概型:
我们将具有:
(1)试验中所有可能出现的基本事件只有有限个;(有限性)
(2)每个基本事件出现的可能性相等.(等可能性)
这样两个特点的概率模型称为古典概率概型,简称古典概型.
2.古典概型计算任何事件的概率计算公式为:
3.求某个随机事件A包含的基本事件的个数和实验中基本事件的总数时常用的方法是列举法(画树状图和列表),注意做到不重不漏.
自小多才学,平生志气高;
别人怀宝剑,我有笔和刀 .
-------《神童诗》
