(苏教版) 高中数学第3章空间向量与立体几何3.1.1空间向量及其线性运算课件 选修2-1(26张)
文档属性
| 名称 | (苏教版) 高中数学第3章空间向量与立体几何3.1.1空间向量及其线性运算课件 选修2-1(26张) |  | |
| 格式 | zip | ||
| 文件大小 | 487.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-23 22:56:34 | ||
图片预览





文档简介
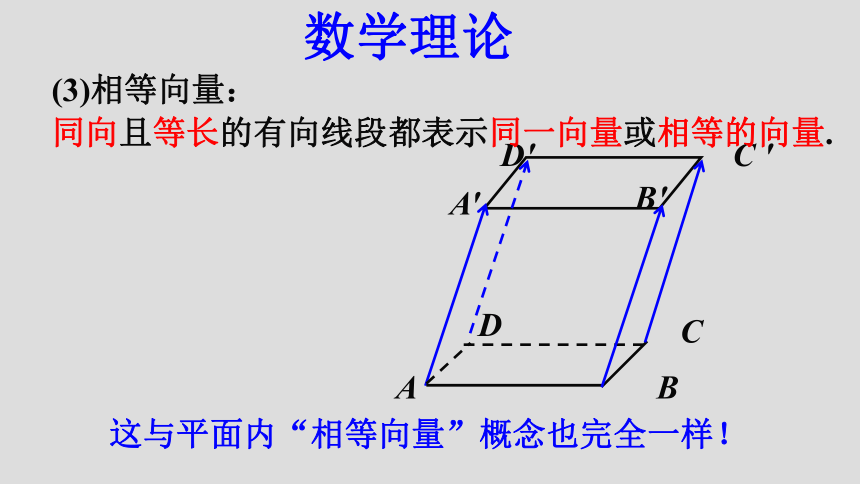
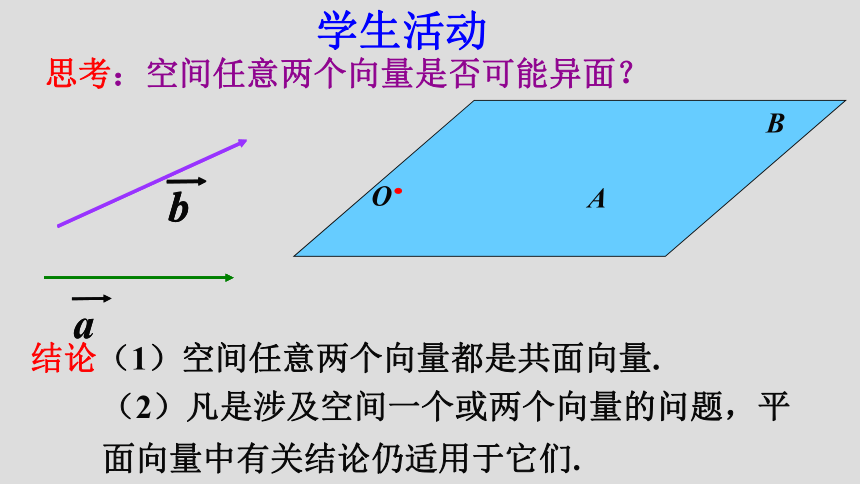
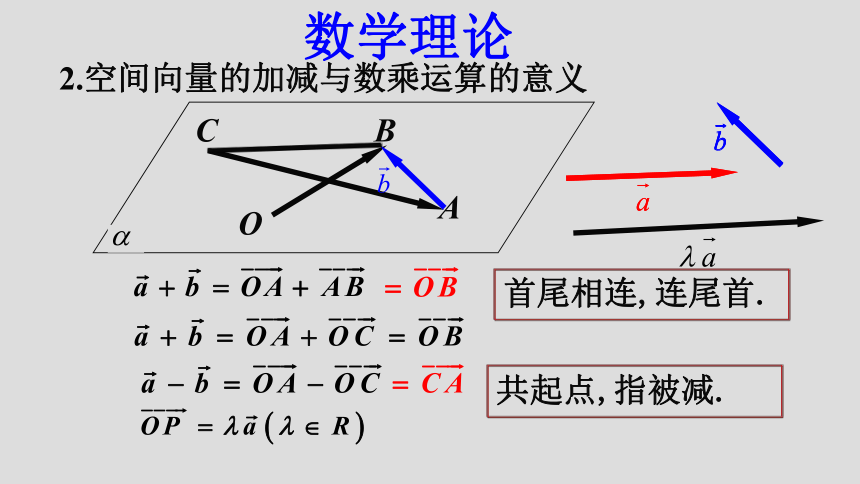
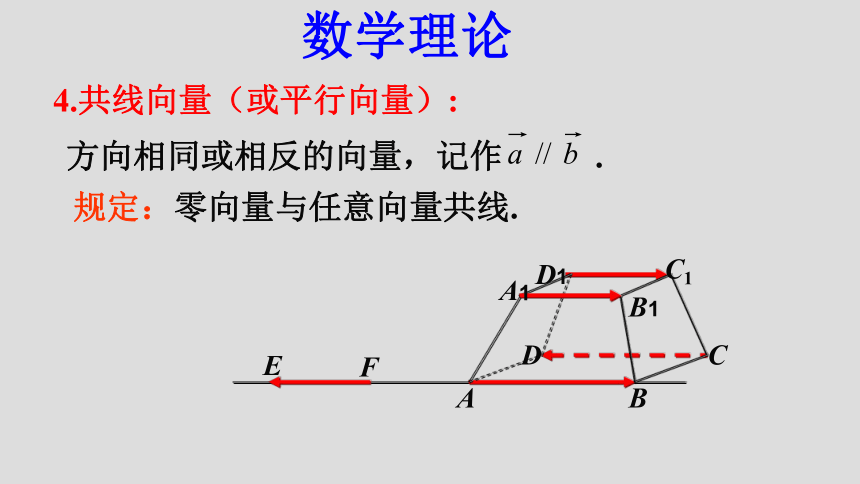
课件26张PPT。3.3.1 空间向量及其线性运算(1)定义:⒈空间向量:在空间,具有大小和方向的量叫做空间向量.(2)表示方法: 数学理论用有向线段表示在定义上,空间向量与平面向量一样!在表示方法上,空间向量与平面向量也一样!都有两个要素:大小、方向(3)相等向量: 数学理论这与平面内“相等向量”概念也完全一样!同向且等长的有向线段都表示同一向量或相等的向量.结论(1)空间任意两个向量都是共面向量.OAB思考:空间任意两个向量是否可能异面? 学生活动(2)凡是涉及空间一个或两个向量的问题,平面向量中有关结论仍适用于它们.ABCO2.空间向量的加减与数乘运算的意义 数学理论首尾相连,连尾首.共起点,指被减.⑴加法交换律:⑵加法结合律:⑶数乘分配律:3.空间向量加法与数乘运算满足如下运算律: 数学理论空间向量加法的结合律 可以借助空间四边形来验证:OBAC 数学理论OBAC探究活动ADCBA1D1C1B1思考:请问在如图的长方体AC1中,推广:首尾相连,连尾首.规定:零向量与任意向量共线. 4.共线向量(或平行向量): 数学理论BADCB1A1D1C1FE方向相同或相反的向量,记作 . 5.共线向量定理 数学理论 空间任意两个向量 , 共线 的充要条件是存在实数λ使 .思考:(1)设 是两个不共线的空间向量,A,B,C 三点共线,(2)若 能得到A,B,C,D四点共线吗?(3)若 能得到A,B,C三点共线吗?6不能能证明:ABCDA′B′C′D′已知:平行六面体
求证:探究活动ABCDA′B′C′D ′ 始点相同的三个不共面向量之和,等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所表示的向量
-------平行六面体法则平行四边形法则 平行六面体法则由二维到三维 数学理论CAC1BB1A1例1 如图,在三棱柱ABC-A1B1C1中,M是BB1的中点,化简下列各式:数学运用变式1 如图,已知M,N分别是空间四边形ABCD的对角线AC和BD的中点,求证: .数学运用BACDNM变式1 如图,已知M,N分别是空间四边形ABCD的对角线AC和BD的中点,求证: .数学运用BACDNM证法一:取BD的中点G,连结MG,NG,G又M,N分别是AC和BD的中点,变式1 如图,已知M,N分别是空间四边形ABCD的对角线AC和BD的中点,求证: .数学运用BACDNM证法二:取AD的中点G,连结MG,NG,G又M,N分别是AC和BD的中点,变式1 如图,已知M,N分别是空间四边形ABCD的对角线AC和BD的中点,求证: .数学运用BACDNM证法三:∵M,N分别是AC和BD的中点,例2 如图,在长方体OADB-CA?D?B?中,OA=6,OB=8,OC=4,OI=OJ=OK=1,点E,F分别是DB,D?B?的中点,设 .试用向量
表示 . DOABCA?D?EFB?IJK684解例2 如图,在长方体OADB-CA?D?B?中,OA=6,OB=8,OC=4,OI=OJ=OK=1,点E,F分别是DB,D?B?的中点,设 .试用向量
表示 . DOABCA?D?EFB?IJK684解例2 如图,在长方体OADB-CA?D?B?中,OA=6,OB=8,OC=4,OI=OJ=OK=1,点E,F分别是DB,D?B?的中点,设 .试用向量 表示 . DOABCA?D?EFB?IJK684思考:将长方体的8个顶点选作始点和终点的向量中,与向量 相等的向量有几个?与向量 互为相反向量的向量有几个?与向量 共线的向量有几个? . 变式2 如图,在单位正方体ABCD-A1B1C1D1中,点E,
F分别是棱B1C1,CC1的中点,设
试用向量 表示 ,并判断向量
是否共线,四边形EFDA1是否为梯形. 数学运用ADCBA1D1C1B1EF课本第83—84第2、5、6题当堂检测(巩固练习)归纳小结本节课你学习了哪些知识?
掌握了哪些技能?交送:
课本P83 练习第3题、第6题
选做:
1.正方体AC1中,点E,F分别为棱BC和A1D1的中点,求证:四边形DEB1F为平行四边形.布置作业2.空间四边形ABCD中,M、G分别是BC、CD边的中点,化简:谢谢!
求证:探究活动ABCDA′B′C′D ′ 始点相同的三个不共面向量之和,等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所表示的向量
-------平行六面体法则平行四边形法则 平行六面体法则由二维到三维 数学理论CAC1BB1A1例1 如图,在三棱柱ABC-A1B1C1中,M是BB1的中点,化简下列各式:数学运用变式1 如图,已知M,N分别是空间四边形ABCD的对角线AC和BD的中点,求证: .数学运用BACDNM变式1 如图,已知M,N分别是空间四边形ABCD的对角线AC和BD的中点,求证: .数学运用BACDNM证法一:取BD的中点G,连结MG,NG,G又M,N分别是AC和BD的中点,变式1 如图,已知M,N分别是空间四边形ABCD的对角线AC和BD的中点,求证: .数学运用BACDNM证法二:取AD的中点G,连结MG,NG,G又M,N分别是AC和BD的中点,变式1 如图,已知M,N分别是空间四边形ABCD的对角线AC和BD的中点,求证: .数学运用BACDNM证法三:∵M,N分别是AC和BD的中点,例2 如图,在长方体OADB-CA?D?B?中,OA=6,OB=8,OC=4,OI=OJ=OK=1,点E,F分别是DB,D?B?的中点,设 .试用向量
表示 . DOABCA?D?EFB?IJK684解例2 如图,在长方体OADB-CA?D?B?中,OA=6,OB=8,OC=4,OI=OJ=OK=1,点E,F分别是DB,D?B?的中点,设 .试用向量
表示 . DOABCA?D?EFB?IJK684解例2 如图,在长方体OADB-CA?D?B?中,OA=6,OB=8,OC=4,OI=OJ=OK=1,点E,F分别是DB,D?B?的中点,设 .试用向量 表示 . DOABCA?D?EFB?IJK684思考:将长方体的8个顶点选作始点和终点的向量中,与向量 相等的向量有几个?与向量 互为相反向量的向量有几个?与向量 共线的向量有几个? . 变式2 如图,在单位正方体ABCD-A1B1C1D1中,点E,
F分别是棱B1C1,CC1的中点,设
试用向量 表示 ,并判断向量
是否共线,四边形EFDA1是否为梯形. 数学运用ADCBA1D1C1B1EF课本第83—84第2、5、6题当堂检测(巩固练习)归纳小结本节课你学习了哪些知识?
掌握了哪些技能?交送:
课本P83 练习第3题、第6题
选做:
1.正方体AC1中,点E,F分别为棱BC和A1D1的中点,求证:四边形DEB1F为平行四边形.布置作业2.空间四边形ABCD中,M、G分别是BC、CD边的中点,化简:谢谢!
