【备考2019中考数学学案】第五单元 四边形专项训练
文档属性
| 名称 | 【备考2019中考数学学案】第五单元 四边形专项训练 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-24 09:03:21 | ||
图片预览



文档简介
第五单元 四边形
专 项 训 练
类型一 证明线段的等积式
1.如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE。
(1)求证:BE·AD=CD·AE;
(2)根据图形的特点,猜想可能等于哪两条线段的比(只须写出图中已有线段的一组即可),并说明理由。
2.在矩形ABCD中,E为CD的中点,H为BE上的一点,=3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F。
(1)求证:EC·BH=BG·EH;
(2)若∠CGF=90°时,求的值.
3.如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.
求证:(1)∠PBC=∠CBD;
(2)BC2=AB·BD。
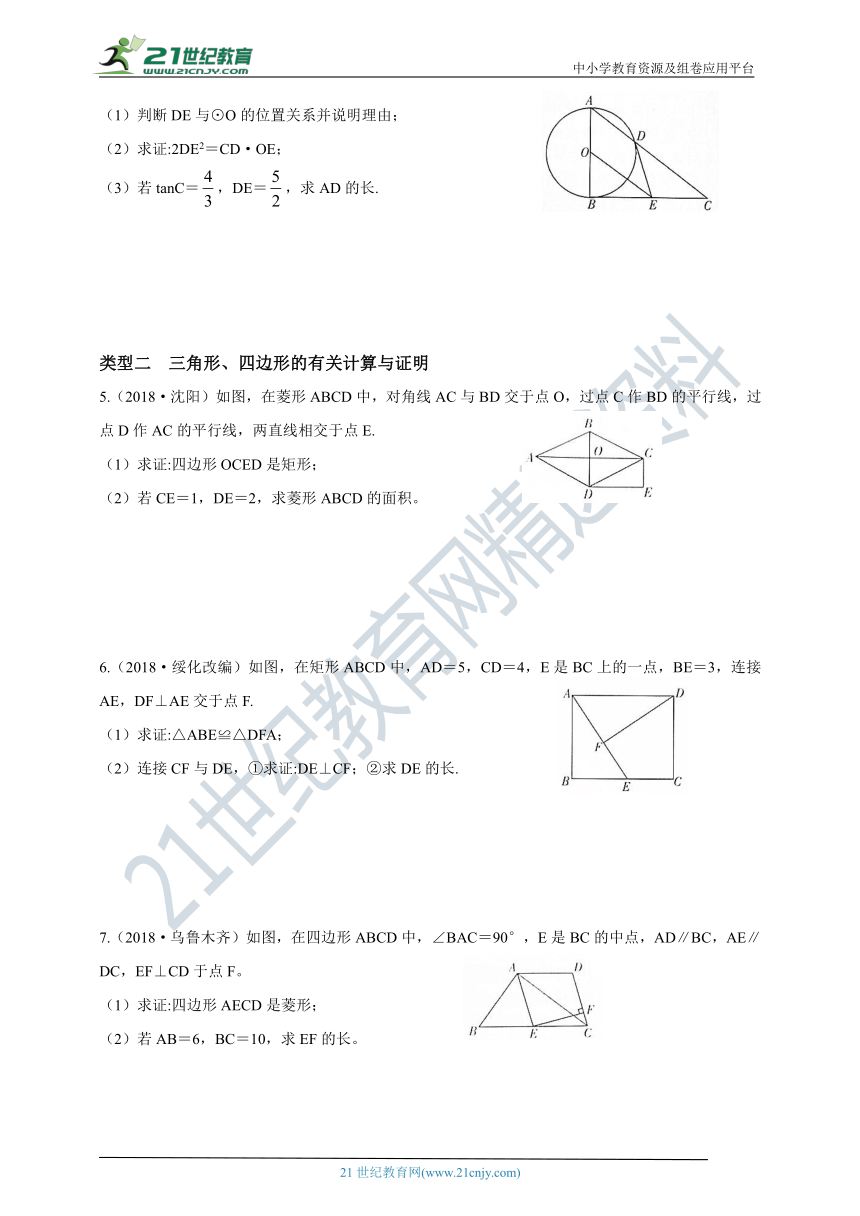
4.(2018·内江)如图,以Rt△ABC的直角边AB为直径作⊙O交斜边AC于点D,过圆心O作OE∥AC,交BC于点E,连接DE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:2DE2=CD·OE;
(3)若tanC=,DE=,求AD的长.
类型二 三角形、四边形的有关计算与证明
5.(2018·沈阳)如图,在菱形ABCD中,对角线AC与BD交于点O,过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,求菱形ABCD的面积。
6.(2018·绥化改编)如图,在矩形ABCD中,AD=5,CD=4,E是BC上的一点,BE=3,连接AE,DF⊥AE交于点F.
(1)求证:△ABE≌△DFA;
(2)连接CF与DE,①求证:DE⊥CF;②求DE的长.
7.(2018·乌鲁木齐)如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F。
(1)求证:四边形AECD是菱形;
(2)若AB=6,BC=10,求EF的长。
8.(2018·南宁)如图,在 ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证: ABCD是菱形;
(2)若AB=5,AC=6,求 ABCD的面积。
9.(2017·南通)如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD,BE,BC于点P,O,Q,连接BP,EQ。
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长。
10.(2018· 重庆)如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,交AC于点G.
(1)若AH=3,HE=1,求△ABE的面积;
(2)若∠ACB=45°,求证:DF=CG.
11.(2016·东营)如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B,C分别在边AD,AF上,此时BD=CF,BD⊥CF成立。
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H。
①求证:BD⊥CF;
②当AB=2,AD=3时,求线段DH的长。
12.(2018·威海)如图①,在四边形BCDE中,BC⊥CD,DE⊥CD,AB⊥AE,垂足分别为C,D,A,BC≠AC,点M,N,F分别为AB,AE,BE的中点,连接MN,MF,NF。
(1)如图②,当BC=4,DE=5,tan∠FMN=1时,求的值;
(2)若tan∠FMN=,BC=4,则可求出图中哪些线段的长?写出解答过程;
(3)连接CM,DN,CF,DF,试证明△FMC与△DNF全等;
(4)在(3)的条件下,图中还有哪些其他的全等三角形?请直接写出.
参考答案及解析
类型一 证明线段的等积式
1.(1)证明:∵∠DAE=∠BAC,∴∠DAC=∠BAE。又∵∠BDC=∠BAC,∠DOC=∠AOB,
∴∠DCA=∠EBA。∴△ABE∽△ACD,∴. BE·AD=CD·AE 。
(2)解:.理由:由△ABE∽△ACD得.又∵∠DAE=∠BAC,
∴△ABC∽△AED.故有.
2.(1)证明:∵四边形ABCD为矩形,∴AB∥CD,∴∠HBG=∠HEC,∠HGB=∠HCE,
∴△BHG∽EHC,∴,∴EC·BH=bG·EH.
(2)过点E作EM⊥AB于点M.∴EM=BC=AD,AM=DE.∵E为CD的中点,∴DE=CE.
设DE=CE=3a,则AB=CD=6a,
由(1)得=3,∴BG=CE=a,∴AG=5a.
∵∠EDF=90°=∠CGF,∠DEF=∠GEC,∴△DEF∽△GEC .
∴.∴EG·EF=DE·EC。∵CD∥AB,∴,∴.
∴EF=EG.∴EG·EG=3a·3a,解得EG=a.
在Rt△EMG中,GM=2a,∴EM==a.∴BC=a.
∴.
3.证明:(1)连接OC,∵PC是⊙O的切线,∴OC⊥PD,
∵BD⊥PC,∴OC∥BD,∴∠DBC=∠BCO.
∵OC=OB,∴∠OBC=∠OCB.∴∠PBC=∠CBD.
(2)连接AC,∵AB是半圆O的直径,∴∠ACB=90°,∴∠ACB=∠CDB.
∵∠PBC=∠CBD.∴△ACB∽△CDB.∴.∴BC2=AB·BD.
4.解:(1)DE是⊙O的切线,理由:如图,连接OD,BD,∵AB是⊙O的直径,
∴∠ADB=∠BDC=90°∵OE∥AC,OA=OB,∴BE=CE,∴DE=BE=CE。
∴∠DBE=∠BDE.∵OB=OD,∴∠OBD=∠ODB,∴∠ODE=∠OBE=90°。
∵点D在⊙O上,∴DE是⊙O的切线;
(2)∵∠BDC=∠ABC=90°,∠C=∠C,
∴△BCD∽△ACB,∴,∴BC2=CD·AC.
由(1)知DE=BE=CE=BC,∴4DE2=CD·AC.
由(1)知,OE是△ABC是中位线,∴AC=2OE,∴4DE2=CD·2OE,∴2DE2=CD·OE.
(3)∵DE=∴BC=5。在Rt△BCD中,tanC==,设CD=3x,BD=4x,
根据勾股定理得,(3x)2+(4x)2=25,∴x=-1(舍)或x=1,∴BD=4,CD=3。
由(2)知,BC2=CD·AC,∴AC=,∴AD=AC-CD=。
类型二 三角形、四边形的有关计算与证明
5.(1)证明:四边形ABCD为菱形;∴AC⊥BD,∴∠COD=90°,∵CE∥OD,DE∥OC,
∴四边形OCED为平行四边形,∵∠COD=90°,平行四边形OCED为矩形。
(2)解:由(1)得四边形ODEC是矩形,因此OD=CE,OC=DE,
因此AC=2DE=4,BD=2CE=2,所以菱形ABCD面积等于AC·BD=×4×2=4。
6.(1)证明:∵四边形ABCD是矩形,∴∠B=90°,AD∥BC,∴∠AEB=∠DAF,
∵DF⊥AE,∴∠DFA=90°,∴∠B=∠DFA。在Rt△ABE中,AB=DC=4,BE=3,
∴AE=5,∴AE=AD,∴△ABE≌△DFA.
(2)①连接DE与CF相交于点H。
∵△ABE≌△DFA∴DF=AB=CD=4,AF=BE=3,
∴EF=CE=2,DE⊥CF.
②由①知,∠DCH+∠HDC=∠DEC+∠HDC=90°。∴∠DCH=∠DEC。
在Rt△DEC中,CD=4,CE=2DE=2。
7.(1)证明:∵AD∥BC,AE∥DC,∴四边形AECD是平行四边形。
在Rt△ABC中,∠BAC=90°,E是BC的中点,∴BE=EC=AE,∴四边形AECD是菱形。
(2)解:过点A作AH⊥BC于点H,
在Rt△ABC中,∠BAC=90°,AB=6,BC=10,由勾股定理得AC=8。
再根据面积关系,有S△ABC=BC·AH=AB·AC,∴AH=。
∵点E是BC的中点,BC=10,四边形AECD是菱形,∴CD=CE=5,
S菱形AECD=CD·EF=CE·AH,∴EF=AH=。
8.(1)证明:∵四边形ABCD是平行四边形,∴∠B=∠D.∵AE⊥BC,AF⊥DC,
∴∠AEB=∠AFD=90°。又∵BE=DF,∴△AEB≌△AFD(ASA)。
∴AB=AD,∴四边形ABCD是菱形。
(2)解:连接BD交AC于点O、∵由(1)知四边形ABCD是菱形,AC=6,
∴AC⊥BD,AO=OC=AC=,∵AB=5,AO=3。
在Rt△AOB中,BO=。
∴BD=2BO=8,∴S菱形ABCD=AC·BD=×6×8=24。
9.(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠PEB=∠EBQ。
∵PQ垂直平分BE,∴OE=OB,∠POE=∠QOB=90°,∴△OPE≌△OQB。
∴OP=OQ.∴四边形BPEQ是平行四边形。∵PQ⊥BE,∴四边形BPEQ是菱形。
(2)解:OB=OE,BF=AF=AB=3,∴OF∥AE。
∴∠OFB=∠A-90o,∠BOF=∠PEO。
设OFB=9-x,∵OF+OB=9,OB=9-x.
在Rt△OBF中,(x-9)2= x2+32,解得x=4.
∴∠BFO=∠POE=90°,∠BOF=∠PEO,∴△BFO∽△POE,∴,
即OP=·OE=∴PQ=2OP=.
10.(1)解:∵AH=3,HE=1,∴AB=AE=AH+HE=4。
又∵在Rt△ABH中,BH==,
∴S△ABE= AE×BH=×4×=2。
(2)证明:过点A作AM⊥BC于点M,交BG于点K,过点G作GN⊥BC交于点N.
∴∠AMB=∠AME=∠BNG=90°。 ∵∠ACB=45°,∴∠MAC=∠ACB=∠NGC=45°。
∵AB=AE,∴BM=ME=BE,∠BAM=∠EAM。∵AE⊥BG,∴∠AHK=90°。
∵∠AHK+∠MAE+∠AKH=180°,∠AMB+∠NBG+∠BKM=180°,∴∠MAE=∠NBG。
设∠BAM=∠MAE=∠NBG=a,
∴∠BAG=∠MAC+∠BAM=45°+a,∠BGA=∠ACB+∠NBG=45°+a,
∴∠BAG=∠BGA,∴AB=BG,∴AE=BG,∴△AME≌△BNG(AAS)。
∴ME=NG,∵NG=NC,∴GC=NG=ME=BE,即BE,即BE=GC。
∵O为AC的中点,∴OA=OC。∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,
∴∠OAF=∠OCE,∠AFO=∠CEO。∴△AFO≌△CEO(AAS),∴AF=CE。
∴AD-AF=BC-CE,即DF=BE=GC.
11.解:(1)BD=CF成立。理由如下:由题意得,∠CAF=∠BAD=θ,
在△CAF和△BAD中,,∴△CAF≌△BAD,∴BD=CF。
(2)①由(1)得△CAF≌△BAD,∴∠CFA=∠BDA。∵∠FNH=∠DNA,∠DNA+∠NDA=90°,∴∠CFA+∠FNH=90°,∴∠FHN=90°,即BD⊥CF。
②如图,连接DF,延长AB交DF于M,∵四边形ADEF是正方形,AD=3,AB=2,
∴AM=DM=3, BM=AM-AB=1.DB==,∵∠MAD=∠MDA=45o,
∴∠AMD=90°,又∠DHF=90°,∠MDB=∠HDF,∴△DMB∽△DHF,
∴,即,解得,DH=。
12.解:(1)M,N,F分别是AB,AE,BE的中点,∴BM=NF=MA,MF=AN=NE.
∴四边形MANF是平行四边形,又∵BA⊥AE,∴平行四边形MANF是矩形 .
又∵tan∠FMN=1,∴=1,即FN=FM。
∴矩形MANF为正方形,∴AB=AE。
∵∠1+∠2=90°,∠2+∠3=90o,∴∠1=∠3;∵∠C=∠D=90o,∴△ABC≌△EAD(AAS),∴BC=AD,CA=DE。∵BC=4,DE=5,∴。
(2)可求线段AD的长。
由(1)知,四边形MANF为矩形,FN=AB,MF=AE;∵tan∠FMN=,即=,
∴ 。∵∠1=∠3,∠BCA=∠ADE=90°, ∴△ABC∽△EAD,∴。
∵BC=4,∴=,∴AD=8。
(3)∵BC⊥CD,DE⊥CD.∴△ABC与△ADE都是直角三角形。
∵M,N分别是AB,AE中点,∴.BM=CM,NA=ND.∴∠4=2∠1,∠5=2∠3.
∵∠1=∠3,∴∠4=∠5,∴∠FMC=90°+∠4,∠FND=90o+∠5,∴∠FMC=∠FND.
∵FM=DN,CM=NF.∴△FMC≌△DNF(SAS)
(4)△BMF≌△NFM≌△MAN≌△FNE。
专 项 训 练
类型一 证明线段的等积式
1.如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE。
(1)求证:BE·AD=CD·AE;
(2)根据图形的特点,猜想可能等于哪两条线段的比(只须写出图中已有线段的一组即可),并说明理由。
2.在矩形ABCD中,E为CD的中点,H为BE上的一点,=3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F。
(1)求证:EC·BH=BG·EH;
(2)若∠CGF=90°时,求的值.
3.如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.
求证:(1)∠PBC=∠CBD;
(2)BC2=AB·BD。
4.(2018·内江)如图,以Rt△ABC的直角边AB为直径作⊙O交斜边AC于点D,过圆心O作OE∥AC,交BC于点E,连接DE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:2DE2=CD·OE;
(3)若tanC=,DE=,求AD的长.
类型二 三角形、四边形的有关计算与证明
5.(2018·沈阳)如图,在菱形ABCD中,对角线AC与BD交于点O,过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,求菱形ABCD的面积。
6.(2018·绥化改编)如图,在矩形ABCD中,AD=5,CD=4,E是BC上的一点,BE=3,连接AE,DF⊥AE交于点F.
(1)求证:△ABE≌△DFA;
(2)连接CF与DE,①求证:DE⊥CF;②求DE的长.
7.(2018·乌鲁木齐)如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F。
(1)求证:四边形AECD是菱形;
(2)若AB=6,BC=10,求EF的长。
8.(2018·南宁)如图,在 ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证: ABCD是菱形;
(2)若AB=5,AC=6,求 ABCD的面积。
9.(2017·南通)如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD,BE,BC于点P,O,Q,连接BP,EQ。
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长。
10.(2018· 重庆)如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,交AC于点G.
(1)若AH=3,HE=1,求△ABE的面积;
(2)若∠ACB=45°,求证:DF=CG.
11.(2016·东营)如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B,C分别在边AD,AF上,此时BD=CF,BD⊥CF成立。
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H。
①求证:BD⊥CF;
②当AB=2,AD=3时,求线段DH的长。
12.(2018·威海)如图①,在四边形BCDE中,BC⊥CD,DE⊥CD,AB⊥AE,垂足分别为C,D,A,BC≠AC,点M,N,F分别为AB,AE,BE的中点,连接MN,MF,NF。
(1)如图②,当BC=4,DE=5,tan∠FMN=1时,求的值;
(2)若tan∠FMN=,BC=4,则可求出图中哪些线段的长?写出解答过程;
(3)连接CM,DN,CF,DF,试证明△FMC与△DNF全等;
(4)在(3)的条件下,图中还有哪些其他的全等三角形?请直接写出.
参考答案及解析
类型一 证明线段的等积式
1.(1)证明:∵∠DAE=∠BAC,∴∠DAC=∠BAE。又∵∠BDC=∠BAC,∠DOC=∠AOB,
∴∠DCA=∠EBA。∴△ABE∽△ACD,∴. BE·AD=CD·AE 。
(2)解:.理由:由△ABE∽△ACD得.又∵∠DAE=∠BAC,
∴△ABC∽△AED.故有.
2.(1)证明:∵四边形ABCD为矩形,∴AB∥CD,∴∠HBG=∠HEC,∠HGB=∠HCE,
∴△BHG∽EHC,∴,∴EC·BH=bG·EH.
(2)过点E作EM⊥AB于点M.∴EM=BC=AD,AM=DE.∵E为CD的中点,∴DE=CE.
设DE=CE=3a,则AB=CD=6a,
由(1)得=3,∴BG=CE=a,∴AG=5a.
∵∠EDF=90°=∠CGF,∠DEF=∠GEC,∴△DEF∽△GEC .
∴.∴EG·EF=DE·EC。∵CD∥AB,∴,∴.
∴EF=EG.∴EG·EG=3a·3a,解得EG=a.
在Rt△EMG中,GM=2a,∴EM==a.∴BC=a.
∴.
3.证明:(1)连接OC,∵PC是⊙O的切线,∴OC⊥PD,
∵BD⊥PC,∴OC∥BD,∴∠DBC=∠BCO.
∵OC=OB,∴∠OBC=∠OCB.∴∠PBC=∠CBD.
(2)连接AC,∵AB是半圆O的直径,∴∠ACB=90°,∴∠ACB=∠CDB.
∵∠PBC=∠CBD.∴△ACB∽△CDB.∴.∴BC2=AB·BD.
4.解:(1)DE是⊙O的切线,理由:如图,连接OD,BD,∵AB是⊙O的直径,
∴∠ADB=∠BDC=90°∵OE∥AC,OA=OB,∴BE=CE,∴DE=BE=CE。
∴∠DBE=∠BDE.∵OB=OD,∴∠OBD=∠ODB,∴∠ODE=∠OBE=90°。
∵点D在⊙O上,∴DE是⊙O的切线;
(2)∵∠BDC=∠ABC=90°,∠C=∠C,
∴△BCD∽△ACB,∴,∴BC2=CD·AC.
由(1)知DE=BE=CE=BC,∴4DE2=CD·AC.
由(1)知,OE是△ABC是中位线,∴AC=2OE,∴4DE2=CD·2OE,∴2DE2=CD·OE.
(3)∵DE=∴BC=5。在Rt△BCD中,tanC==,设CD=3x,BD=4x,
根据勾股定理得,(3x)2+(4x)2=25,∴x=-1(舍)或x=1,∴BD=4,CD=3。
由(2)知,BC2=CD·AC,∴AC=,∴AD=AC-CD=。
类型二 三角形、四边形的有关计算与证明
5.(1)证明:四边形ABCD为菱形;∴AC⊥BD,∴∠COD=90°,∵CE∥OD,DE∥OC,
∴四边形OCED为平行四边形,∵∠COD=90°,平行四边形OCED为矩形。
(2)解:由(1)得四边形ODEC是矩形,因此OD=CE,OC=DE,
因此AC=2DE=4,BD=2CE=2,所以菱形ABCD面积等于AC·BD=×4×2=4。
6.(1)证明:∵四边形ABCD是矩形,∴∠B=90°,AD∥BC,∴∠AEB=∠DAF,
∵DF⊥AE,∴∠DFA=90°,∴∠B=∠DFA。在Rt△ABE中,AB=DC=4,BE=3,
∴AE=5,∴AE=AD,∴△ABE≌△DFA.
(2)①连接DE与CF相交于点H。
∵△ABE≌△DFA∴DF=AB=CD=4,AF=BE=3,
∴EF=CE=2,DE⊥CF.
②由①知,∠DCH+∠HDC=∠DEC+∠HDC=90°。∴∠DCH=∠DEC。
在Rt△DEC中,CD=4,CE=2DE=2。
7.(1)证明:∵AD∥BC,AE∥DC,∴四边形AECD是平行四边形。
在Rt△ABC中,∠BAC=90°,E是BC的中点,∴BE=EC=AE,∴四边形AECD是菱形。
(2)解:过点A作AH⊥BC于点H,
在Rt△ABC中,∠BAC=90°,AB=6,BC=10,由勾股定理得AC=8。
再根据面积关系,有S△ABC=BC·AH=AB·AC,∴AH=。
∵点E是BC的中点,BC=10,四边形AECD是菱形,∴CD=CE=5,
S菱形AECD=CD·EF=CE·AH,∴EF=AH=。
8.(1)证明:∵四边形ABCD是平行四边形,∴∠B=∠D.∵AE⊥BC,AF⊥DC,
∴∠AEB=∠AFD=90°。又∵BE=DF,∴△AEB≌△AFD(ASA)。
∴AB=AD,∴四边形ABCD是菱形。
(2)解:连接BD交AC于点O、∵由(1)知四边形ABCD是菱形,AC=6,
∴AC⊥BD,AO=OC=AC=,∵AB=5,AO=3。
在Rt△AOB中,BO=。
∴BD=2BO=8,∴S菱形ABCD=AC·BD=×6×8=24。
9.(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠PEB=∠EBQ。
∵PQ垂直平分BE,∴OE=OB,∠POE=∠QOB=90°,∴△OPE≌△OQB。
∴OP=OQ.∴四边形BPEQ是平行四边形。∵PQ⊥BE,∴四边形BPEQ是菱形。
(2)解:OB=OE,BF=AF=AB=3,∴OF∥AE。
∴∠OFB=∠A-90o,∠BOF=∠PEO。
设OFB=9-x,∵OF+OB=9,OB=9-x.
在Rt△OBF中,(x-9)2= x2+32,解得x=4.
∴∠BFO=∠POE=90°,∠BOF=∠PEO,∴△BFO∽△POE,∴,
即OP=·OE=∴PQ=2OP=.
10.(1)解:∵AH=3,HE=1,∴AB=AE=AH+HE=4。
又∵在Rt△ABH中,BH==,
∴S△ABE= AE×BH=×4×=2。
(2)证明:过点A作AM⊥BC于点M,交BG于点K,过点G作GN⊥BC交于点N.
∴∠AMB=∠AME=∠BNG=90°。 ∵∠ACB=45°,∴∠MAC=∠ACB=∠NGC=45°。
∵AB=AE,∴BM=ME=BE,∠BAM=∠EAM。∵AE⊥BG,∴∠AHK=90°。
∵∠AHK+∠MAE+∠AKH=180°,∠AMB+∠NBG+∠BKM=180°,∴∠MAE=∠NBG。
设∠BAM=∠MAE=∠NBG=a,
∴∠BAG=∠MAC+∠BAM=45°+a,∠BGA=∠ACB+∠NBG=45°+a,
∴∠BAG=∠BGA,∴AB=BG,∴AE=BG,∴△AME≌△BNG(AAS)。
∴ME=NG,∵NG=NC,∴GC=NG=ME=BE,即BE,即BE=GC。
∵O为AC的中点,∴OA=OC。∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,
∴∠OAF=∠OCE,∠AFO=∠CEO。∴△AFO≌△CEO(AAS),∴AF=CE。
∴AD-AF=BC-CE,即DF=BE=GC.
11.解:(1)BD=CF成立。理由如下:由题意得,∠CAF=∠BAD=θ,
在△CAF和△BAD中,,∴△CAF≌△BAD,∴BD=CF。
(2)①由(1)得△CAF≌△BAD,∴∠CFA=∠BDA。∵∠FNH=∠DNA,∠DNA+∠NDA=90°,∴∠CFA+∠FNH=90°,∴∠FHN=90°,即BD⊥CF。
②如图,连接DF,延长AB交DF于M,∵四边形ADEF是正方形,AD=3,AB=2,
∴AM=DM=3, BM=AM-AB=1.DB==,∵∠MAD=∠MDA=45o,
∴∠AMD=90°,又∠DHF=90°,∠MDB=∠HDF,∴△DMB∽△DHF,
∴,即,解得,DH=。
12.解:(1)M,N,F分别是AB,AE,BE的中点,∴BM=NF=MA,MF=AN=NE.
∴四边形MANF是平行四边形,又∵BA⊥AE,∴平行四边形MANF是矩形 .
又∵tan∠FMN=1,∴=1,即FN=FM。
∴矩形MANF为正方形,∴AB=AE。
∵∠1+∠2=90°,∠2+∠3=90o,∴∠1=∠3;∵∠C=∠D=90o,∴△ABC≌△EAD(AAS),∴BC=AD,CA=DE。∵BC=4,DE=5,∴。
(2)可求线段AD的长。
由(1)知,四边形MANF为矩形,FN=AB,MF=AE;∵tan∠FMN=,即=,
∴ 。∵∠1=∠3,∠BCA=∠ADE=90°, ∴△ABC∽△EAD,∴。
∵BC=4,∴=,∴AD=8。
(3)∵BC⊥CD,DE⊥CD.∴△ABC与△ADE都是直角三角形。
∵M,N分别是AB,AE中点,∴.BM=CM,NA=ND.∴∠4=2∠1,∠5=2∠3.
∵∠1=∠3,∴∠4=∠5,∴∠FMC=90°+∠4,∠FND=90o+∠5,∴∠FMC=∠FND.
∵FM=DN,CM=NF.∴△FMC≌△DNF(SAS)
(4)△BMF≌△NFM≌△MAN≌△FNE。
同课章节目录
