2.3中心对称和中心对称图形(一)(20张PPT)
文档属性
| 名称 | 2.3中心对称和中心对称图形(一)(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-25 00:00:00 | ||
图片预览








文档简介
2.3中心对称和中心对称图形(一)
第
2
三
角
形
章
1.了解中心对称、对称中心和对称点的概念。
2.理解中心对称的性质。
3.掌握运用中心对称的性质作图的方法。
教学目标:
一、创设情境,复习导入
s.
这两组图片中的两个图形具有什么共同的特征?
成轴对称
再观察一组图片
1.他们还关于某条线成轴对称吗?
不成轴对称
2.两个图形能否重合?怎样才能重合?
二、讲授新知
重 合
O
A
O
D
B
C
问题1:观察下列图形的运动,说一说它们有什么共同点.
观察与思考
旋转角为180°
即形状和大小一样
知识要点
如果把一个图形(如△ABO)绕定点O旋转180?,它能够与另一个图形(如△CDO)重合(即大小和形状一样),那么就说这两个图形△ABO与图形△CDO关于点O对称或中心对称,点O就是对称中心.
填一填:
如图,△OCD与△OAB关于点O中心对称 ,则____是对称中心,点A与_____是对称点, 点B与____是对称点.
O
B
C
A
D
O
C
D
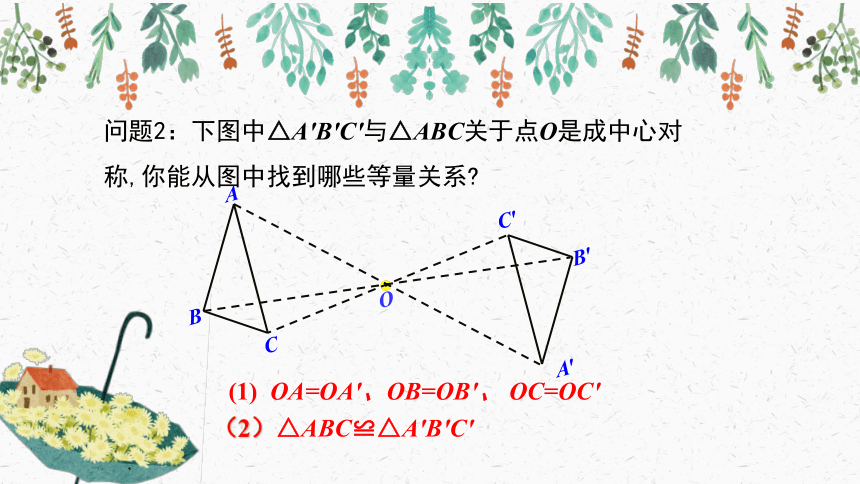
问题2:下图中△A′B′C′与△ABC关于点O是成中心对称,你能从图中找到哪些等量关系?
A′
B′
C′
A
B
C
O
(1) OA=OA′、OB=OB′、 OC=OC′
(2)△ABC≌△A′B′C′
1.成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.(即对称点与对称中心三点共线)
2.中心对称的两个图形是全等形.
知识要点
中心对称的性质
A
O
A'
第一步:连接AO,
第二步:延长AO至A',使OA'=OA,
例1 (1)已知A点和O点,画出点A关于点O的对称点A'.
则A'是所求的点.
三、典例精析
(2)已知线段AB和O点,画出线段AB关于点O的对称线段A' B' .
B'
A'
A
B
O
简记为:一连接;二延长;三截取等长;四连线.
(3)如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
A′
C′
B′
△A′B′C′为所求作的三角形
B
A
C
O
考考你:1.如图,已知△ABC与△A′B′C′中心对称,找出它们的对称中心O.
A
B
C
A′
B′
C′
解法1:根据观察,B、B′应是对应点,连接BB′,用刻度尺找出BB′的中点O,则点O即为所求(如图).
A
B
C
A′
B′
C′
O
O
解法2:根据观察,B、B′及C、C′应是两组对应点,连接BB′、CC′,BB′、CC′相交于点O,则点O即为所求(如图).
A
B
C
A′
B′
C′
注意:如果限制只用直尺作图,我们用解法2.
四、课堂练习
1、判断。
(1)线段AB的中点是点A和点B的对称中心。( )
(2)关于中心对称的两个图形是全等图形。( )
(3)两个全等的图形一定关于中心对称。( )
2、画出三角形ABC关于点A成中心对称的图形。
√
√
×
B'
A'
C'
3、如图,四边形ABCD与四边形A'B'C'D'关于某点对称,找出他们的对称中心。
text
text
text
text
O
五、课堂小结
中心对称
概念
1.有一个对称中心——点
2.图形绕中心旋转180°。
性质
作图
应用1:作中心对称图形;
应用2:找出对称中心.
1.对称中心与两对称点三点共线;
2.成中心对称的两个图形是全等图形。
六、作业
1、课堂作业:教材54页习题2.3第1题
2、家庭作业:学法第30页
谢谢观看!
第
2
三
角
形
章
1.了解中心对称、对称中心和对称点的概念。
2.理解中心对称的性质。
3.掌握运用中心对称的性质作图的方法。
教学目标:
一、创设情境,复习导入
s.
这两组图片中的两个图形具有什么共同的特征?
成轴对称
再观察一组图片
1.他们还关于某条线成轴对称吗?
不成轴对称
2.两个图形能否重合?怎样才能重合?
二、讲授新知
重 合
O
A
O
D
B
C
问题1:观察下列图形的运动,说一说它们有什么共同点.
观察与思考
旋转角为180°
即形状和大小一样
知识要点
如果把一个图形(如△ABO)绕定点O旋转180?,它能够与另一个图形(如△CDO)重合(即大小和形状一样),那么就说这两个图形△ABO与图形△CDO关于点O对称或中心对称,点O就是对称中心.
填一填:
如图,△OCD与△OAB关于点O中心对称 ,则____是对称中心,点A与_____是对称点, 点B与____是对称点.
O
B
C
A
D
O
C
D
问题2:下图中△A′B′C′与△ABC关于点O是成中心对称,你能从图中找到哪些等量关系?
A′
B′
C′
A
B
C
O
(1) OA=OA′、OB=OB′、 OC=OC′
(2)△ABC≌△A′B′C′
1.成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.(即对称点与对称中心三点共线)
2.中心对称的两个图形是全等形.
知识要点
中心对称的性质
A
O
A'
第一步:连接AO,
第二步:延长AO至A',使OA'=OA,
例1 (1)已知A点和O点,画出点A关于点O的对称点A'.
则A'是所求的点.
三、典例精析
(2)已知线段AB和O点,画出线段AB关于点O的对称线段A' B' .
B'
A'
A
B
O
简记为:一连接;二延长;三截取等长;四连线.
(3)如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
A′
C′
B′
△A′B′C′为所求作的三角形
B
A
C
O
考考你:1.如图,已知△ABC与△A′B′C′中心对称,找出它们的对称中心O.
A
B
C
A′
B′
C′
解法1:根据观察,B、B′应是对应点,连接BB′,用刻度尺找出BB′的中点O,则点O即为所求(如图).
A
B
C
A′
B′
C′
O
O
解法2:根据观察,B、B′及C、C′应是两组对应点,连接BB′、CC′,BB′、CC′相交于点O,则点O即为所求(如图).
A
B
C
A′
B′
C′
注意:如果限制只用直尺作图,我们用解法2.
四、课堂练习
1、判断。
(1)线段AB的中点是点A和点B的对称中心。( )
(2)关于中心对称的两个图形是全等图形。( )
(3)两个全等的图形一定关于中心对称。( )
2、画出三角形ABC关于点A成中心对称的图形。
√
√
×
B'
A'
C'
3、如图,四边形ABCD与四边形A'B'C'D'关于某点对称,找出他们的对称中心。
text
text
text
text
O
五、课堂小结
中心对称
概念
1.有一个对称中心——点
2.图形绕中心旋转180°。
性质
作图
应用1:作中心对称图形;
应用2:找出对称中心.
1.对称中心与两对称点三点共线;
2.成中心对称的两个图形是全等图形。
六、作业
1、课堂作业:教材54页习题2.3第1题
2、家庭作业:学法第30页
谢谢观看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
