2019年中考科学总复习专题六能量转化综合计算(精讲)(课件 13张PPT)
文档属性
| 名称 | 2019年中考科学总复习专题六能量转化综合计算(精讲)(课件 13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2019-03-26 08:05:59 | ||
图片预览




文档简介
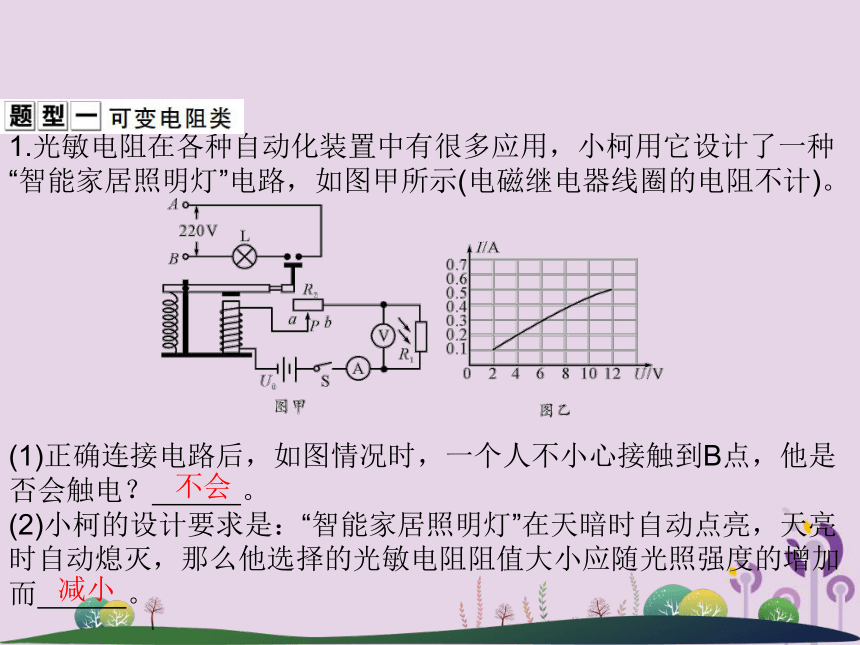
课件13张PPT。专题六 能量转化综合计算1.光敏电阻在各种自动化装置中有很多应用,小柯用它设计了一种“智能家居照明灯”电路,如图甲所示(电磁继电器线圈的电阻不计)。
?
(1)正确连接电路后,如图情况时,一个人不小心接触到B点,他是否会触电? 。
(2)小柯的设计要求是:“智能家居照明灯”在天暗时自动点亮,天亮时自动熄灭,那么他选择的光敏电阻阻值大小应随光照强度的增加而 。不会减小(3)保持光照强度不变,闭合开关S后,滑片P由a端向b端移动过程中,电流表示数I与电压表示数U的关系如图乙所示,计算滑动变阻器的最大阻值是多少欧?(电源电压U0不变)
(3)解:当滑片位于b端时,电路为光敏电阻的简单电路,电压表测电源的电压,由图可知电源的电压U=12 V;当滑片位于a端时滑动变阻器与光敏电阻串联,电压表测光敏电阻两端的电压,电流表测电路中的电流,由图像可知,I=0.1 A,U光敏=2 V,则电路中的总电阻R总= =120Ω,
光敏电阻的阻值R光敏= =20Ω,
滑动变阻器的最大阻值Rab=R总-R光敏=120Ω-20Ω=100Ω。2.有一种电能辅助式太阳能热水器,晴天时它接收
太阳能的真空镀膜管的总有效面积约为1.5 m2,能
将接收的太阳能的50%转化为水的内能;阴雨天时
用电加热,电热管上标有“220 V 1000 W”。
[水的散热忽略不计,水的比热容c=4.2×103 J/(kg·℃)]
(1)晴天时,假设每平方米的真空镀膜管1 h内得到4.2×106 J的太阳能,如果每天接收太阳能的时间以10 h计算,可以将100 kg、初温为15℃的水加热到多少摄氏度?
解:(1)水所吸收的热量:Q吸=4.2×106 J/(m2·h)×1.5 m2×
10 h×50%=3.15×107 J,
由Q=cm(t-t0)可得水能加热到的温度:
t= =90℃;(2)阴雨天时需用电加热,如果所消耗的电能全部转化为水的内能,热水器在额定电压下工作时,将上述同样质量、初温的水加热到45℃需多长时间?
(2)所消耗的电能全部转化为水的内能,W=Q吸′=cm′(t-t0)=4.2×103 J/(kg·℃)×100 kg×(45℃-15℃)=1.26×107 J,
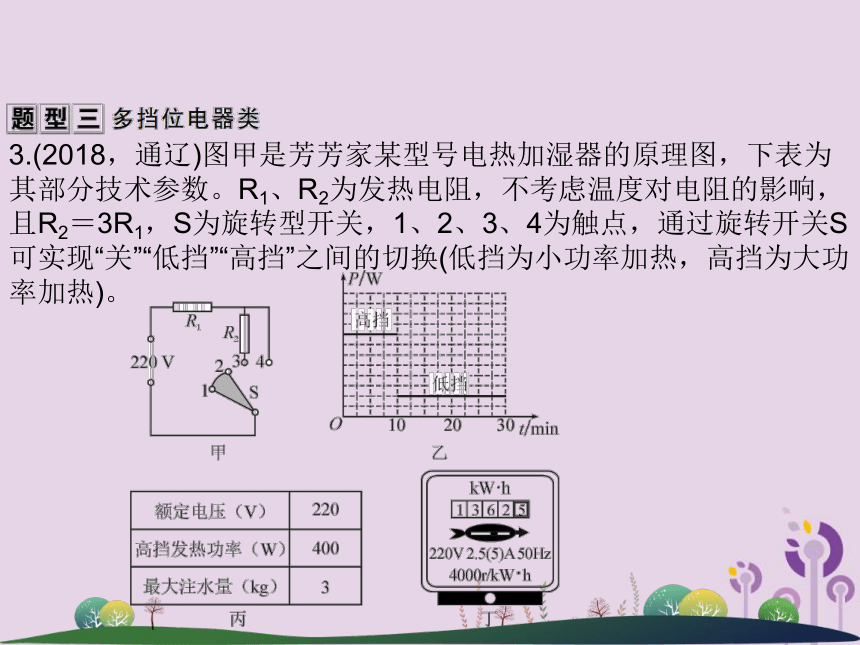
由 可得用电能所需要的时间:3.(2018,通辽)图甲是芳芳家某型号电热加湿器的原理图,下表为其部分技术参数。R1、R2为发热电阻,不考虑温度对电阻的影响,且R2=3R1,S为旋转型开关,1、2、3、4为触点,通过旋转开关S可实现“关”“低挡”“高挡”之间的切换(低挡为小功率加热,高挡为大功率加热)。(1)求加湿器处于低挡位置时的发热功率。
解:(1)由图1知,开关S接“1、2触点”时,电路断路,为关;接“2、3触点”时两电阻串联,接“3、4触点”时只有R1接入电路;电源电压一定,由 可知,接“2、3触点”时电阻最大,总功
率最小,为低挡;接“3、4触点”时电阻最小,总功率最大,为高挡;由表格数据知,高挡功率:P高=400W,由 可得
R1的阻值:R1= =121Ω;由题知,R2=3R1,
则低挡的发热功率:P低= =100W(2)某次使用加湿器工作时,加湿器注水仓中加注冷水已达到最大注水量。如图乙所示是该次使用加湿器工作30min的图像,请计算加湿器在高挡正常工作时消耗的电能。如果电阻R1在此次高挡加热时产生的热量全部被水吸收,可以使注水仓中冷水的温度升高多少℃?[计算结果保留整数,水的比热容为4.2×103J/(kg·℃)]
(2)由图2知,工作30min时,其中高挡工作时间为10min,低挡工作时间为20min,则在高挡正常工作时消耗的电能:W高=P高t高=400W×10×60s=2.4×105J。如果电阻R1在此次高挡加热时产生的热量全部被水吸收,即Q=W=2.4×105J。
由Q=cmΔt可得,水升高的温度:Δt=(3)一天,芳芳断开家中其他所有用电器,只接通加湿器在低挡加热,发现家中如图丙所示的电能表的转盘在5min内转了27圈,求此时电阻R2的实际加热功率是多少?
(3)“4000r/(kW·h)”的意义为:每消耗1kW·h的电能,电能表的转盘就转过4000r,则电能表的转盘转过27r时,加湿器在5分钟消耗的电能:W′= =0.00675kW·h,加湿器在低挡加热的
实际功率: =81W。加湿器在低挡加热,此时两电阻串联,则R总=R1+R2=R1+3R1=4R1=4×121Ω=484Ω,由P=I2R可得,此时电路的实际电流: ,
R2的阻值:R2=3R1=3×121Ω=363Ω,此时电阻R2的实际加热功率: 。4.某电动公交车的部分数据如表所示:
当该公交车电池储存的能量降低到充满电时的10%以下时,就需要再次充电。求:
(1)该公交车完成一次充电续驶里程(某一速度匀速行驶)180 km中,若消耗的电能都用于水平行驶做功,则该车行驶时受到的阻力多大?
解:(1)由表格中数据知,电池充电一次的电能Q=UIt,电动公交车匀速行驶,阻力与牵引力平衡,即f=F,牵引力做功W=Fs=fs,公交车电池储存的能量降低到充满电时的10%以下时,就需要再次充电,所以90%W=Q,即:UIt×90%=Fs=fs,
即:400 V×250 A×3600 s×0.9=f×180×1000 m,f=1800 N;
(2)公交车站充电桩给公交车充电的功率为4×104 W,则若该公交车进站时还剩20%的电能,此时进行充电,充满一次电要多长时间?
(2)公交车进站时还剩20%的电能,此时进行充电,由W=Pt和Q=UIt可得:
P充t充=UIt×80%,4×104 W×t充=400 V×250 A×1h×0.8,即:t充=2 h;(3)该公交车的运行线路没有明显的上下坡,运行1趟(从始发站到终点站)全程20 km。经测算,公交车以某一速度匀速行驶运行1趟,因停车需损失4×106 J的电能。则该车充满一次电最多能跑几趟该公交线路?
(3)行驶1趟公交车耗能:
W=Fs′+W损=fs′+W损=1800 N×2×104 m+4×106 J=4.0×107 J,
充满一次电最多能跑趟数:
(4)实际情况下,该公交车在其运行线路上连续可行驶路程比第(3)问的计算结果更大还是更小?
(4)实际情况下,该公交车在其运行线路上连续可行驶路程比第(3)问的计算结果更小,因为电池提供电能还有能量的损耗,不可能全部用来做功。
?
(1)正确连接电路后,如图情况时,一个人不小心接触到B点,他是否会触电? 。
(2)小柯的设计要求是:“智能家居照明灯”在天暗时自动点亮,天亮时自动熄灭,那么他选择的光敏电阻阻值大小应随光照强度的增加而 。不会减小(3)保持光照强度不变,闭合开关S后,滑片P由a端向b端移动过程中,电流表示数I与电压表示数U的关系如图乙所示,计算滑动变阻器的最大阻值是多少欧?(电源电压U0不变)
(3)解:当滑片位于b端时,电路为光敏电阻的简单电路,电压表测电源的电压,由图可知电源的电压U=12 V;当滑片位于a端时滑动变阻器与光敏电阻串联,电压表测光敏电阻两端的电压,电流表测电路中的电流,由图像可知,I=0.1 A,U光敏=2 V,则电路中的总电阻R总= =120Ω,
光敏电阻的阻值R光敏= =20Ω,
滑动变阻器的最大阻值Rab=R总-R光敏=120Ω-20Ω=100Ω。2.有一种电能辅助式太阳能热水器,晴天时它接收
太阳能的真空镀膜管的总有效面积约为1.5 m2,能
将接收的太阳能的50%转化为水的内能;阴雨天时
用电加热,电热管上标有“220 V 1000 W”。
[水的散热忽略不计,水的比热容c=4.2×103 J/(kg·℃)]
(1)晴天时,假设每平方米的真空镀膜管1 h内得到4.2×106 J的太阳能,如果每天接收太阳能的时间以10 h计算,可以将100 kg、初温为15℃的水加热到多少摄氏度?
解:(1)水所吸收的热量:Q吸=4.2×106 J/(m2·h)×1.5 m2×
10 h×50%=3.15×107 J,
由Q=cm(t-t0)可得水能加热到的温度:
t= =90℃;(2)阴雨天时需用电加热,如果所消耗的电能全部转化为水的内能,热水器在额定电压下工作时,将上述同样质量、初温的水加热到45℃需多长时间?
(2)所消耗的电能全部转化为水的内能,W=Q吸′=cm′(t-t0)=4.2×103 J/(kg·℃)×100 kg×(45℃-15℃)=1.26×107 J,
由 可得用电能所需要的时间:3.(2018,通辽)图甲是芳芳家某型号电热加湿器的原理图,下表为其部分技术参数。R1、R2为发热电阻,不考虑温度对电阻的影响,且R2=3R1,S为旋转型开关,1、2、3、4为触点,通过旋转开关S可实现“关”“低挡”“高挡”之间的切换(低挡为小功率加热,高挡为大功率加热)。(1)求加湿器处于低挡位置时的发热功率。
解:(1)由图1知,开关S接“1、2触点”时,电路断路,为关;接“2、3触点”时两电阻串联,接“3、4触点”时只有R1接入电路;电源电压一定,由 可知,接“2、3触点”时电阻最大,总功
率最小,为低挡;接“3、4触点”时电阻最小,总功率最大,为高挡;由表格数据知,高挡功率:P高=400W,由 可得
R1的阻值:R1= =121Ω;由题知,R2=3R1,
则低挡的发热功率:P低= =100W(2)某次使用加湿器工作时,加湿器注水仓中加注冷水已达到最大注水量。如图乙所示是该次使用加湿器工作30min的图像,请计算加湿器在高挡正常工作时消耗的电能。如果电阻R1在此次高挡加热时产生的热量全部被水吸收,可以使注水仓中冷水的温度升高多少℃?[计算结果保留整数,水的比热容为4.2×103J/(kg·℃)]
(2)由图2知,工作30min时,其中高挡工作时间为10min,低挡工作时间为20min,则在高挡正常工作时消耗的电能:W高=P高t高=400W×10×60s=2.4×105J。如果电阻R1在此次高挡加热时产生的热量全部被水吸收,即Q=W=2.4×105J。
由Q=cmΔt可得,水升高的温度:Δt=(3)一天,芳芳断开家中其他所有用电器,只接通加湿器在低挡加热,发现家中如图丙所示的电能表的转盘在5min内转了27圈,求此时电阻R2的实际加热功率是多少?
(3)“4000r/(kW·h)”的意义为:每消耗1kW·h的电能,电能表的转盘就转过4000r,则电能表的转盘转过27r时,加湿器在5分钟消耗的电能:W′= =0.00675kW·h,加湿器在低挡加热的
实际功率: =81W。加湿器在低挡加热,此时两电阻串联,则R总=R1+R2=R1+3R1=4R1=4×121Ω=484Ω,由P=I2R可得,此时电路的实际电流: ,
R2的阻值:R2=3R1=3×121Ω=363Ω,此时电阻R2的实际加热功率: 。4.某电动公交车的部分数据如表所示:
当该公交车电池储存的能量降低到充满电时的10%以下时,就需要再次充电。求:
(1)该公交车完成一次充电续驶里程(某一速度匀速行驶)180 km中,若消耗的电能都用于水平行驶做功,则该车行驶时受到的阻力多大?
解:(1)由表格中数据知,电池充电一次的电能Q=UIt,电动公交车匀速行驶,阻力与牵引力平衡,即f=F,牵引力做功W=Fs=fs,公交车电池储存的能量降低到充满电时的10%以下时,就需要再次充电,所以90%W=Q,即:UIt×90%=Fs=fs,
即:400 V×250 A×3600 s×0.9=f×180×1000 m,f=1800 N;
(2)公交车站充电桩给公交车充电的功率为4×104 W,则若该公交车进站时还剩20%的电能,此时进行充电,充满一次电要多长时间?
(2)公交车进站时还剩20%的电能,此时进行充电,由W=Pt和Q=UIt可得:
P充t充=UIt×80%,4×104 W×t充=400 V×250 A×1h×0.8,即:t充=2 h;(3)该公交车的运行线路没有明显的上下坡,运行1趟(从始发站到终点站)全程20 km。经测算,公交车以某一速度匀速行驶运行1趟,因停车需损失4×106 J的电能。则该车充满一次电最多能跑几趟该公交线路?
(3)行驶1趟公交车耗能:
W=Fs′+W损=fs′+W损=1800 N×2×104 m+4×106 J=4.0×107 J,
充满一次电最多能跑趟数:
(4)实际情况下,该公交车在其运行线路上连续可行驶路程比第(3)问的计算结果更大还是更小?
(4)实际情况下,该公交车在其运行线路上连续可行驶路程比第(3)问的计算结果更小,因为电池提供电能还有能量的损耗,不可能全部用来做功。
同课章节目录
