江苏省江都区嘶马中学2019年七年级数学第7章平面图形的认识(二)复习教案
文档属性
| 名称 | 江苏省江都区嘶马中学2019年七年级数学第7章平面图形的认识(二)复习教案 |  | |
| 格式 | zip | ||
| 文件大小 | 223.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-26 22:45:40 | ||
图片预览


文档简介
第7章《平面图形的认识(二)》复习教案
教学目标:
1.知道同位角的含义,能识别出同位角;能利用同位角、内错角、同旁内角关系说明两直线平行;能利用两线平行求解角度;
2.通过探索两直线平行条件的活动过程,提高对图形的认识能力和分析能力;学会一些简单的说理.
3.能利用同位角、内错角、同旁内角关系说明两直线平行;能利用两线平行求解角度;
教学过程:
知识点整理:
1、我们通常用“//”表示平行.
AB//CD,读作:AB平行于CD
2、同位角、内错角、同旁内角
这两种角都是两条直线被第三条直线所截形成的,因此识别这三种角的关键是认清第三条直线(截线).
同位角特征:①在被截两直线两旁;②在截线的同旁(弄清两个同).
内错角特征:①在被截两直线之间;②在截线的两旁(抓住“之间”与“两旁”).
同位角特征:①在被截两直线之间;②在截线的同旁(抓住“之间”与“同旁”).
3、两直线平行的条件
⑴同位角相等,两直线平行;
⑵内错角相等,两直线平行;
⑶同旁内角互补,两直线平行.
4、两直线平行的性质
⑴两直线平行,同位角相等,
⑵两直线平行,内错角相等;
⑶两直线平行,同旁内角互补.
5、数学语言
∵a∥b,
∴∠2+ ∠4=180°.
典型例题讲解
题型一:基本知识
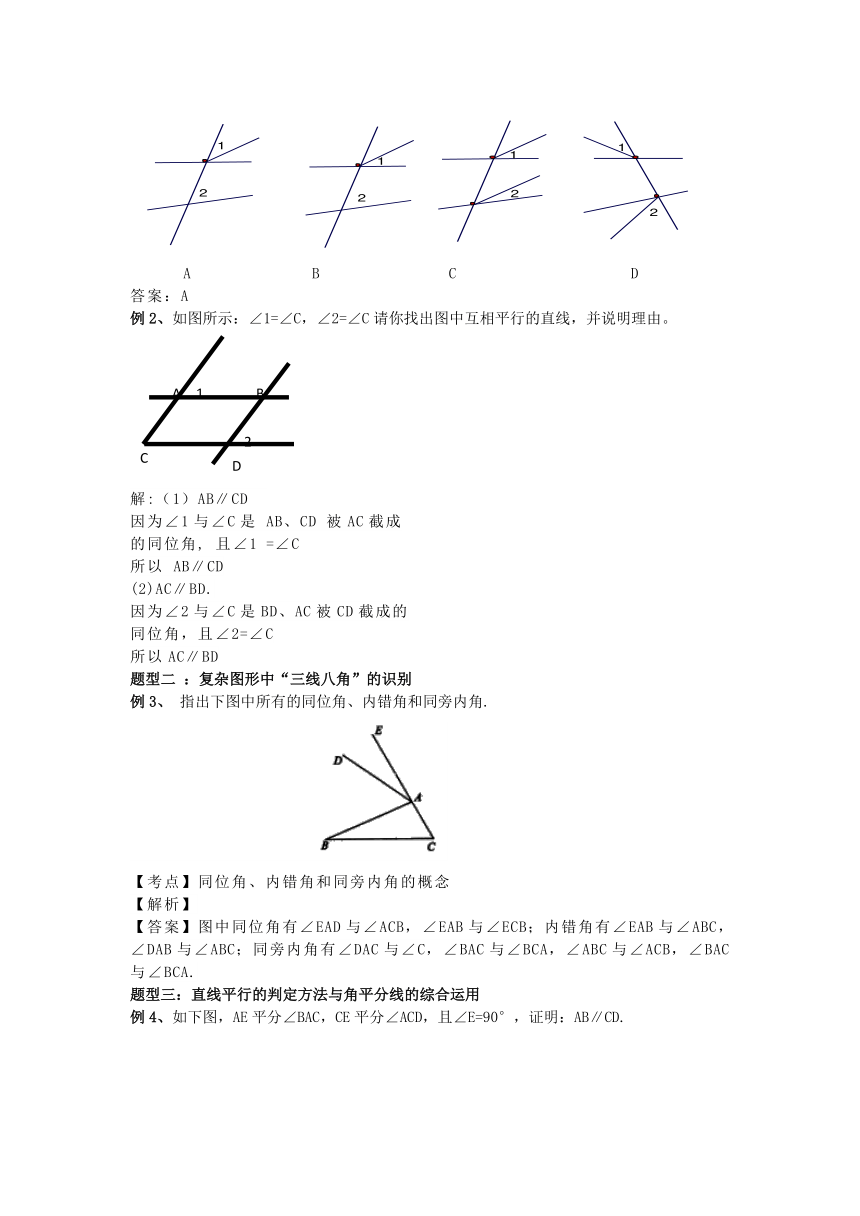
例1、如图,∠1和∠2是同位角的是( )
A B C D
答案:A
例2、如图所示:∠1=∠C,∠2=∠C请你找出图中互相平行的直线,并说明理由。
解:(1)AB∥CD
因为∠1与∠C是 AB、CD 被AC截成
的同位角, 且∠1 =∠C
所以 AB∥CD
(2)AC∥BD.
因为∠2与∠C是BD、AC被CD截成的
同位角,且∠2=∠C
所以AC∥BD
题型二 :复杂图形中“三线八角”的识别
例3、 指出下图中所有的同位角、内错角和同旁内角.
【考点】同位角、内错角和同旁内角的概念
【解析】
【答案】图中同位角有∠EAD与∠ACB,∠EAB与∠ECB;内错角有∠EAB与∠ABC,∠DAB与∠ABC;同旁内角有∠DAC与∠C,∠BAC与∠BCA,∠ABC与∠ACB,∠BAC与∠BCA.
题型三:直线平行的判定方法与角平分线的综合运用
例4、如下图,AE平分∠BAC,CE平分∠ACD,且∠E=90°,证明:AB∥CD.
【考点】平行线性质,三角和内角和定理.
【解析】由∠E=90°,得∠1+∠2=90°,又由AE平分∠BAC,CE平分∠ACD,得∠BAC+∠ACD=180°,根据同旁内角互补,两直线平行,即可得AB∥CD.
【答案】因为AE平分∠BAC,CE平分∠ACD(已知),
所以∠1=1/2∠BAC,∠2=1/2∠ACD(角平分线定义);
因为∠E=90°(已知),所以∠1+∠2=90°(三角形内角和定理),
所以∠BAC+∠ACD=2(∠1+∠2)=180°,
所以AB∥CD(同旁内角互补,两直线平行)
【教学建议】由已知条件及三角形内角和是180°得出∠BAC+∠ACD=180°,是解决问题的关键.
题型四、两直线平行的判定的实际中的运用
例5、如图所示,在铺设铁轨时,两条铁轨必须是平行的.已知∠2是直角,那么再测量图中的哪个角(仅限图中已标出的角),就可以判断图中的两条铁轨AB,CD是否平行?为什么?
【考点】通过同位角、内错角和同旁内角判断直线平行.
【解析】只要在测量出∠5或∠6或∠7的度数,如果它们是直角,就可以判断两条铁轨平行.
【答案】因为∠1=∠3=90°,
①如果∠5=90°,则∠3+∠5=180°.
所以AB∥CD(同旁内角互补,两直线平行);
②如果∠6=90°,则∠2=∠6,
所以AB∥CD(同位角相等,两直线平行);
③如果∠7=90°,则∠6=90°.
所以∠2=∠6,
所以AB∥CD(同位角相等,两直线平行).
题型五、平行线的性质
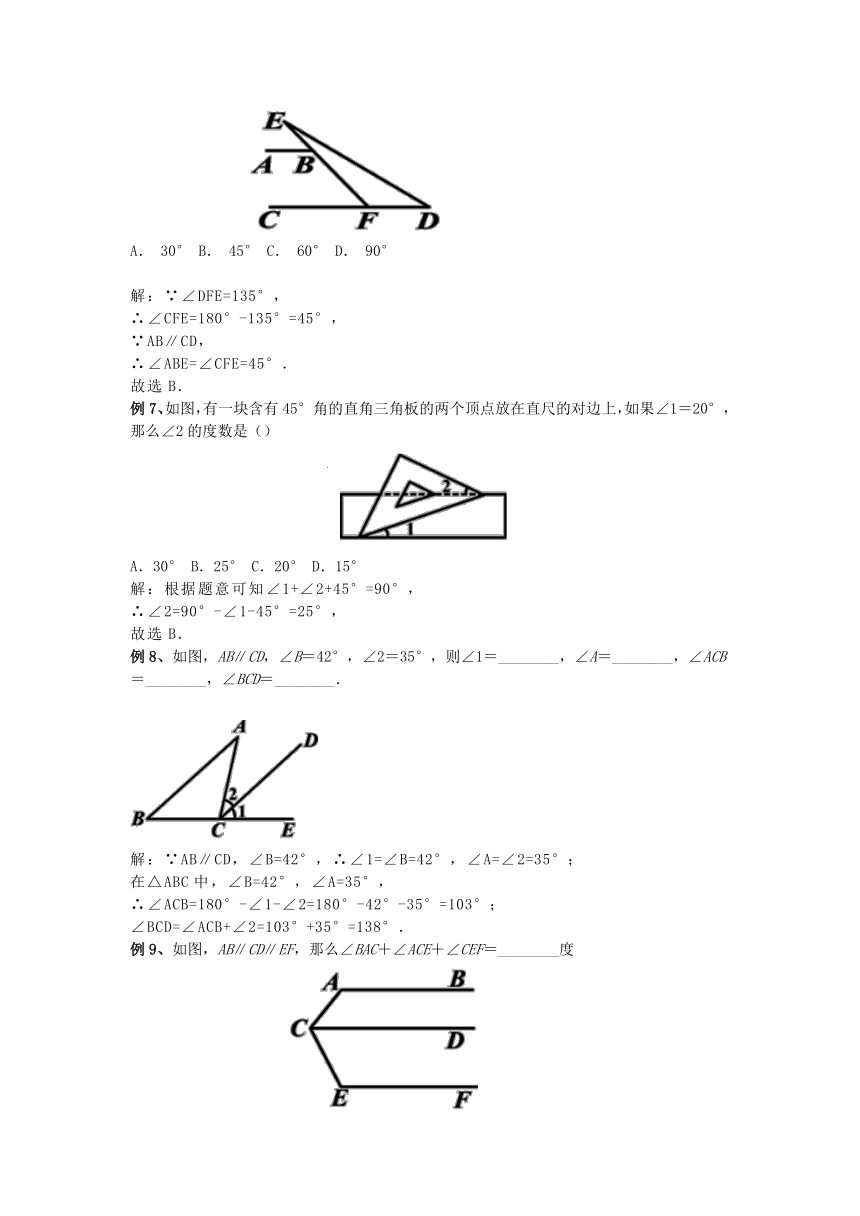
例6、如图,已知AB∥CD,∠DFE=135°,则∠ABE的度数为( )
A. 30° B. 45° C. 60° D. 90°
解:∵∠DFE=135°,
∴∠CFE=180°-135°=45°,
∵AB∥CD,
∴∠ABE=∠CFE=45°.
故选B.
例7、如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2的度数是()
A.30° B.25° C.20° D.15°
解:根据题意可知∠1+∠2+45°=90°,
∴∠2=90°-∠1-45°=25°,
故选B.
例8、如图,AB∥CD,∠B=42°,∠2=35°,则∠1=________,∠A=________,∠ACB=________,∠BCD=________.
解:∵AB∥CD,∠B=42°,∴∠1=∠B=42°,∠A=∠2=35°;
在△ABC中,∠B=42°,∠A=35°,∴∠ACB=180°-∠1-∠2=180°-42°-35°=103°;
∠BCD=∠ACB+∠2=103°+35°=138°.
例9、如图,AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=________度
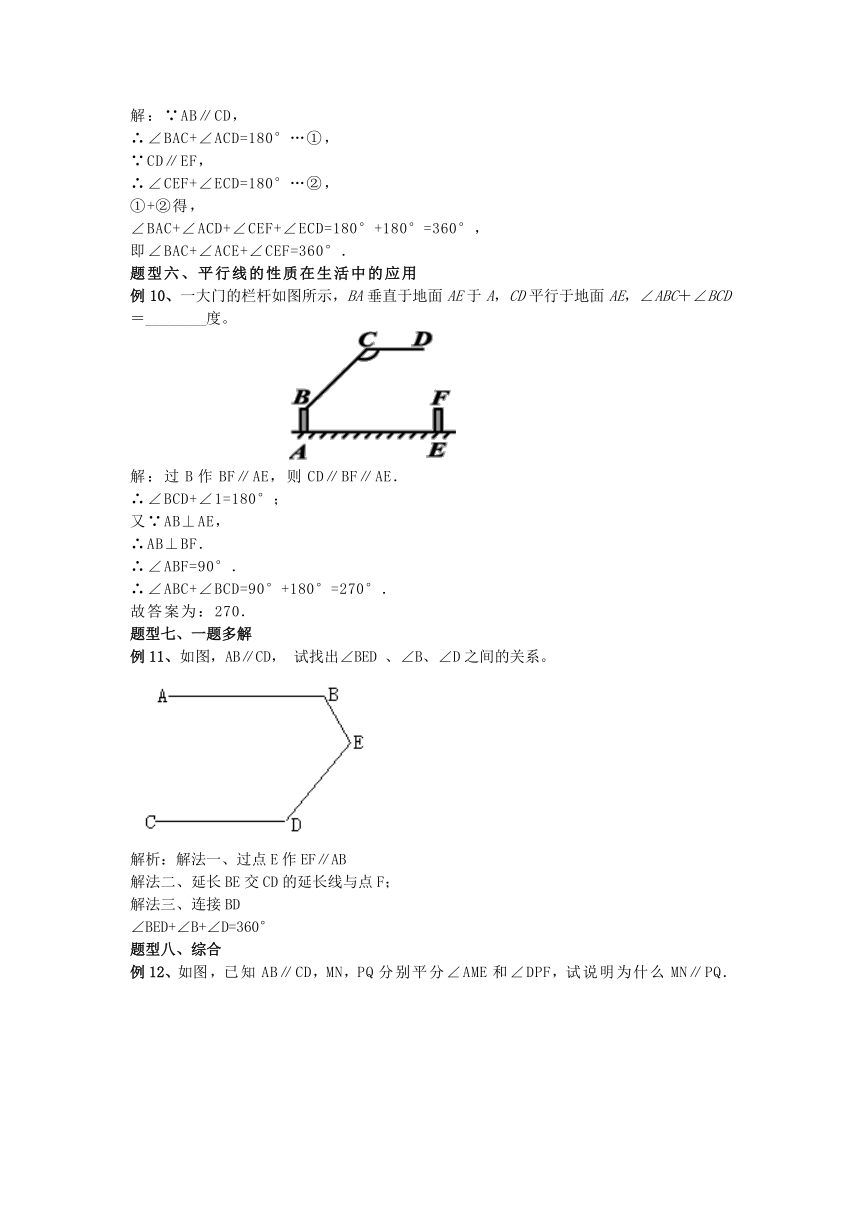
解:∵AB∥CD,
∴∠BAC+∠ACD=180°…①,
∵CD∥EF,
∴∠CEF+∠ECD=180°…②,
①+②得,
∠BAC+∠ACD+∠CEF+∠ECD=180°+180°=360°,
即∠BAC+∠ACE+∠CEF=360°.
题型六、平行线的性质在生活中的应用
例10、一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,∠ABC+∠BCD=________度。
解:过B作BF∥AE,则CD∥BF∥AE.
∴∠BCD+∠1=180°;
又∵AB⊥AE,
∴AB⊥BF.
∴∠ABF=90°.
∴∠ABC+∠BCD=90°+180°=270°.
故答案为:270.
题型七、一题多解
例11、如图,AB∥CD, 试找出∠BED 、∠B、∠D之间的关系。
解析:解法一、过点E作EF∥AB
解法二、延长BE交CD的延长线与点F;
解法三、连接BD
∠BED+∠B+∠D=360°
题型八、综合
例12、如图,已知AB∥CD,MN,PQ分别平分∠AME和∠DPF,试说明为什么MN∥PQ.
证明:∵AB∥CD,
∴∠AME=∠CPE,
又∵∠CPE=∠DPF(对顶角相等),
∴∠AME=∠DPF,
∵MN、PQ分别平分∠AME和∠DPF,
∴∠AMN=∠DPQ.
∵AB∥CD,
∴∠AMP=∠DPM,
∴∠AMP+∠AMN=∠DPM+∠DPQ,即∠NMP=∠QPM,
∴MN∥PQ(内错角相等,两直线平行).
课堂巩固:
1、如图所示直线AB,CD被直线EF所截,
(1)量得∠1=80°,∠2=80°,则判定AB∥CD,根据是 ;
(2)量得∠3=100°,∠4=100°,也判定AB∥CD,根据是 .
解:(1)∵∠1=80°,∠2=80°,
∴∠1=∠2=80°,
∴AB∥CD(同位角相等,两直线平行);
(2)∵∠3=100°,∠4=100°,
∴∠3=∠4,
∴AB∥CD(内错角相等,两直线平行).
故答案为:同位角相等,两直线平行.内错角相等,两直线平行.
2、如图,为了确定一条经过点D且与直线AB平行的直线,小明同学在直线AB上取一点C,在直线AB外取一点E,恰好量得∠2=80°,∠D=50°,∠1=∠3,这时,小明说AB与DE平行了,他说得对吗?为什么?
解:对.
∵∠2=80°,∠1=∠3,
∴2∠1+∠2=180°,
∴∠1=∠3=50°;
∵∠D=50°,
∴∠1=∠D=50°,
∴AB∥DE.
3、如图所示,已知∠ACD=70°,∠ACB=60°,∠ABC=50°.求证:AB∥CD.
证明:∵∠ACD=70°,∠ACB=60°,
∴∠BCD=∠ACB+∠ACD=130°,
∵∠ABC=50°,
∴∠ABC+∠BCD=180°,
∴AB∥CD.
4、如图所示,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°.试说明AB∥EF.
解:过C点作CG∥AB,过点D作DH∥AB,则CG∥DH,
∵∠B=25°,
∴∠BCG=25°,
∵∠BCD=45°,
∴∠GCD=20°,
∵CG∥HD,
∴∠CDH=20°,
∵∠CDE=30°,
∴∠HDE=10°
∴∠HDE=∠E=10°,
∴DH∥EF,
∴DH∥AB,
∴AB∥EF.
如图,AB∥CD,∠B=42°,∠2=35°,则∠1=________,∠A=________,∠ACB=________,∠BCD=________.
解:∵AB∥CD,∠B=42°,∴∠1=∠B=42°,∠A=∠2=35°;
在△ABC中,∠B=42°,∠A=35°,∴∠ACB=180°-∠1-∠2=180°-42°-35°=103°;
∠BCD=∠ACB+∠2=103°+35°=138°.
5、如图,AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=________度
解:∵AB∥CD,
∴∠BAC+∠ACD=180°…①,
∵CD∥EF,
∴∠CEF+∠ECD=180°…②,
①+②得,
∠BAC+∠ACD+∠CEF+∠ECD=180°+180°=360°,
即∠BAC+∠ACE+∠CEF=360°.
6、如图,已知AB∥CD,∠1=∠3,试说明AC∥BD.
证明:因为AB∥CD,
所以∠1=∠2,
又因为∠1=∠3,
所以∠3=∠2.
所以AC∥BD.
7、如图在四边形ABCD中,已知AB∥CD,∠B = 600.
①求∠C的度数;
②由已知条件能否求得∠A的度数?
解: ① ∵ AB∥CD(已知),
∴ ∠B + ∠C= 1800(两直线平行,同旁内角互补).
又∵ ∠B = 600 (已知),
∴∠C = 1200 (等式的性质).
②根据题目的已知条件, 无法求出∠A的度数.
小结:通过本节课的学习,你有什么感悟?
1.知道了同位角的含义,能识别出同位角;
2.能利用同位角、内错角、同旁内角关系说明两直线平行;能利用两线平行求解角度;
3.通过探索两直线平行条件的活动过程,提高对图形的认识能力和分析能力;
学会了一些简单的说理.
课后作业:
1、一辆汽车在笔直的公路上行驶,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是
A第一次向右拐40°,第二次向左拐40°
B第一次向右拐50°,第二次向左拐130°
C第一次向右拐50°,第二次向右拐130°
D第一次向左拐50°,第二次向左拐130°
2、如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4的度数.
3、如图,(1)若∠1=∠2,可以判定哪两条直线平行?根据是什么?(2)若∠1=∠M,可以判定哪两条直线平行?根据是什么?(3)若∠1=∠C,可以判定哪两条直线平行?根据是什么?(4)若∠A+∠3=180°,可以判定哪两条直线平行?根据是什么?
4、如图,已知点D在AB上,DF∥BC,BF平分∠ABC,DE平分∠ADF,你知道DE与BF是否平行吗?试说明理由.
5、如图,一束平行光线AB与DE射向一个水平镜面后被反射,此时
∠l=∠2,∠3=∠4.
(1)∠1与∠3的大小有什么关系?∠2与∠4呢?
(2)反射光线BC与EF也平行吗?
课后作业答案:
1、A
2、∠4=75°.
3、(1)因为∠1=∠2,所以BF∥CE,根据是:内错角相等,两直线平行.
(2)因为∠1=∠M,所以AM∥CE.根据是:内错角相等,两直线平行.
(3)因为∠1=∠C,所以AC∥MD,根据是:同位角相等,两直线平行.
(4)因为∠A+∠3=180°,所以AM∥BF,根据是:同旁内角互补,两直线平行.
4、DE∥BF,理由如下:
∵BF平分∠ABC,DE平分∠ADF,
∴,(角平分线定义).
∵DF∥BC,
∴∠ABC=∠ADF(两直线平行,同位角相等).
∴∠1=∠3(等量代换).
∴DE∥BF(同位角相等,两直线平行).
5、(1)因为AB∥DE,
所以∠1=∠3(两直线平行,同位角相等).
因为∠1=∠2,∠3=∠4,
所以∠2=∠4(等量代换).
(2)因为∠2=∠4,
所以BC∥EF(同位角相等,两直线平行).
b
1
2
a
c
4
A
C
B
D
1
2
教学目标:
1.知道同位角的含义,能识别出同位角;能利用同位角、内错角、同旁内角关系说明两直线平行;能利用两线平行求解角度;
2.通过探索两直线平行条件的活动过程,提高对图形的认识能力和分析能力;学会一些简单的说理.
3.能利用同位角、内错角、同旁内角关系说明两直线平行;能利用两线平行求解角度;
教学过程:
知识点整理:
1、我们通常用“//”表示平行.
AB//CD,读作:AB平行于CD
2、同位角、内错角、同旁内角
这两种角都是两条直线被第三条直线所截形成的,因此识别这三种角的关键是认清第三条直线(截线).
同位角特征:①在被截两直线两旁;②在截线的同旁(弄清两个同).
内错角特征:①在被截两直线之间;②在截线的两旁(抓住“之间”与“两旁”).
同位角特征:①在被截两直线之间;②在截线的同旁(抓住“之间”与“同旁”).
3、两直线平行的条件
⑴同位角相等,两直线平行;
⑵内错角相等,两直线平行;
⑶同旁内角互补,两直线平行.
4、两直线平行的性质
⑴两直线平行,同位角相等,
⑵两直线平行,内错角相等;
⑶两直线平行,同旁内角互补.
5、数学语言
∵a∥b,
∴∠2+ ∠4=180°.
典型例题讲解
题型一:基本知识
例1、如图,∠1和∠2是同位角的是( )
A B C D
答案:A
例2、如图所示:∠1=∠C,∠2=∠C请你找出图中互相平行的直线,并说明理由。
解:(1)AB∥CD
因为∠1与∠C是 AB、CD 被AC截成
的同位角, 且∠1 =∠C
所以 AB∥CD
(2)AC∥BD.
因为∠2与∠C是BD、AC被CD截成的
同位角,且∠2=∠C
所以AC∥BD
题型二 :复杂图形中“三线八角”的识别
例3、 指出下图中所有的同位角、内错角和同旁内角.
【考点】同位角、内错角和同旁内角的概念
【解析】
【答案】图中同位角有∠EAD与∠ACB,∠EAB与∠ECB;内错角有∠EAB与∠ABC,∠DAB与∠ABC;同旁内角有∠DAC与∠C,∠BAC与∠BCA,∠ABC与∠ACB,∠BAC与∠BCA.
题型三:直线平行的判定方法与角平分线的综合运用
例4、如下图,AE平分∠BAC,CE平分∠ACD,且∠E=90°,证明:AB∥CD.
【考点】平行线性质,三角和内角和定理.
【解析】由∠E=90°,得∠1+∠2=90°,又由AE平分∠BAC,CE平分∠ACD,得∠BAC+∠ACD=180°,根据同旁内角互补,两直线平行,即可得AB∥CD.
【答案】因为AE平分∠BAC,CE平分∠ACD(已知),
所以∠1=1/2∠BAC,∠2=1/2∠ACD(角平分线定义);
因为∠E=90°(已知),所以∠1+∠2=90°(三角形内角和定理),
所以∠BAC+∠ACD=2(∠1+∠2)=180°,
所以AB∥CD(同旁内角互补,两直线平行)
【教学建议】由已知条件及三角形内角和是180°得出∠BAC+∠ACD=180°,是解决问题的关键.
题型四、两直线平行的判定的实际中的运用
例5、如图所示,在铺设铁轨时,两条铁轨必须是平行的.已知∠2是直角,那么再测量图中的哪个角(仅限图中已标出的角),就可以判断图中的两条铁轨AB,CD是否平行?为什么?
【考点】通过同位角、内错角和同旁内角判断直线平行.
【解析】只要在测量出∠5或∠6或∠7的度数,如果它们是直角,就可以判断两条铁轨平行.
【答案】因为∠1=∠3=90°,
①如果∠5=90°,则∠3+∠5=180°.
所以AB∥CD(同旁内角互补,两直线平行);
②如果∠6=90°,则∠2=∠6,
所以AB∥CD(同位角相等,两直线平行);
③如果∠7=90°,则∠6=90°.
所以∠2=∠6,
所以AB∥CD(同位角相等,两直线平行).
题型五、平行线的性质
例6、如图,已知AB∥CD,∠DFE=135°,则∠ABE的度数为( )
A. 30° B. 45° C. 60° D. 90°
解:∵∠DFE=135°,
∴∠CFE=180°-135°=45°,
∵AB∥CD,
∴∠ABE=∠CFE=45°.
故选B.
例7、如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2的度数是()
A.30° B.25° C.20° D.15°
解:根据题意可知∠1+∠2+45°=90°,
∴∠2=90°-∠1-45°=25°,
故选B.
例8、如图,AB∥CD,∠B=42°,∠2=35°,则∠1=________,∠A=________,∠ACB=________,∠BCD=________.
解:∵AB∥CD,∠B=42°,∴∠1=∠B=42°,∠A=∠2=35°;
在△ABC中,∠B=42°,∠A=35°,∴∠ACB=180°-∠1-∠2=180°-42°-35°=103°;
∠BCD=∠ACB+∠2=103°+35°=138°.
例9、如图,AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=________度
解:∵AB∥CD,
∴∠BAC+∠ACD=180°…①,
∵CD∥EF,
∴∠CEF+∠ECD=180°…②,
①+②得,
∠BAC+∠ACD+∠CEF+∠ECD=180°+180°=360°,
即∠BAC+∠ACE+∠CEF=360°.
题型六、平行线的性质在生活中的应用
例10、一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,∠ABC+∠BCD=________度。
解:过B作BF∥AE,则CD∥BF∥AE.
∴∠BCD+∠1=180°;
又∵AB⊥AE,
∴AB⊥BF.
∴∠ABF=90°.
∴∠ABC+∠BCD=90°+180°=270°.
故答案为:270.
题型七、一题多解
例11、如图,AB∥CD, 试找出∠BED 、∠B、∠D之间的关系。
解析:解法一、过点E作EF∥AB
解法二、延长BE交CD的延长线与点F;
解法三、连接BD
∠BED+∠B+∠D=360°
题型八、综合
例12、如图,已知AB∥CD,MN,PQ分别平分∠AME和∠DPF,试说明为什么MN∥PQ.
证明:∵AB∥CD,
∴∠AME=∠CPE,
又∵∠CPE=∠DPF(对顶角相等),
∴∠AME=∠DPF,
∵MN、PQ分别平分∠AME和∠DPF,
∴∠AMN=∠DPQ.
∵AB∥CD,
∴∠AMP=∠DPM,
∴∠AMP+∠AMN=∠DPM+∠DPQ,即∠NMP=∠QPM,
∴MN∥PQ(内错角相等,两直线平行).
课堂巩固:
1、如图所示直线AB,CD被直线EF所截,
(1)量得∠1=80°,∠2=80°,则判定AB∥CD,根据是 ;
(2)量得∠3=100°,∠4=100°,也判定AB∥CD,根据是 .
解:(1)∵∠1=80°,∠2=80°,
∴∠1=∠2=80°,
∴AB∥CD(同位角相等,两直线平行);
(2)∵∠3=100°,∠4=100°,
∴∠3=∠4,
∴AB∥CD(内错角相等,两直线平行).
故答案为:同位角相等,两直线平行.内错角相等,两直线平行.
2、如图,为了确定一条经过点D且与直线AB平行的直线,小明同学在直线AB上取一点C,在直线AB外取一点E,恰好量得∠2=80°,∠D=50°,∠1=∠3,这时,小明说AB与DE平行了,他说得对吗?为什么?
解:对.
∵∠2=80°,∠1=∠3,
∴2∠1+∠2=180°,
∴∠1=∠3=50°;
∵∠D=50°,
∴∠1=∠D=50°,
∴AB∥DE.
3、如图所示,已知∠ACD=70°,∠ACB=60°,∠ABC=50°.求证:AB∥CD.
证明:∵∠ACD=70°,∠ACB=60°,
∴∠BCD=∠ACB+∠ACD=130°,
∵∠ABC=50°,
∴∠ABC+∠BCD=180°,
∴AB∥CD.
4、如图所示,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°.试说明AB∥EF.
解:过C点作CG∥AB,过点D作DH∥AB,则CG∥DH,
∵∠B=25°,
∴∠BCG=25°,
∵∠BCD=45°,
∴∠GCD=20°,
∵CG∥HD,
∴∠CDH=20°,
∵∠CDE=30°,
∴∠HDE=10°
∴∠HDE=∠E=10°,
∴DH∥EF,
∴DH∥AB,
∴AB∥EF.
如图,AB∥CD,∠B=42°,∠2=35°,则∠1=________,∠A=________,∠ACB=________,∠BCD=________.
解:∵AB∥CD,∠B=42°,∴∠1=∠B=42°,∠A=∠2=35°;
在△ABC中,∠B=42°,∠A=35°,∴∠ACB=180°-∠1-∠2=180°-42°-35°=103°;
∠BCD=∠ACB+∠2=103°+35°=138°.
5、如图,AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=________度
解:∵AB∥CD,
∴∠BAC+∠ACD=180°…①,
∵CD∥EF,
∴∠CEF+∠ECD=180°…②,
①+②得,
∠BAC+∠ACD+∠CEF+∠ECD=180°+180°=360°,
即∠BAC+∠ACE+∠CEF=360°.
6、如图,已知AB∥CD,∠1=∠3,试说明AC∥BD.
证明:因为AB∥CD,
所以∠1=∠2,
又因为∠1=∠3,
所以∠3=∠2.
所以AC∥BD.
7、如图在四边形ABCD中,已知AB∥CD,∠B = 600.
①求∠C的度数;
②由已知条件能否求得∠A的度数?
解: ① ∵ AB∥CD(已知),
∴ ∠B + ∠C= 1800(两直线平行,同旁内角互补).
又∵ ∠B = 600 (已知),
∴∠C = 1200 (等式的性质).
②根据题目的已知条件, 无法求出∠A的度数.
小结:通过本节课的学习,你有什么感悟?
1.知道了同位角的含义,能识别出同位角;
2.能利用同位角、内错角、同旁内角关系说明两直线平行;能利用两线平行求解角度;
3.通过探索两直线平行条件的活动过程,提高对图形的认识能力和分析能力;
学会了一些简单的说理.
课后作业:
1、一辆汽车在笔直的公路上行驶,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是
A第一次向右拐40°,第二次向左拐40°
B第一次向右拐50°,第二次向左拐130°
C第一次向右拐50°,第二次向右拐130°
D第一次向左拐50°,第二次向左拐130°
2、如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4的度数.
3、如图,(1)若∠1=∠2,可以判定哪两条直线平行?根据是什么?(2)若∠1=∠M,可以判定哪两条直线平行?根据是什么?(3)若∠1=∠C,可以判定哪两条直线平行?根据是什么?(4)若∠A+∠3=180°,可以判定哪两条直线平行?根据是什么?
4、如图,已知点D在AB上,DF∥BC,BF平分∠ABC,DE平分∠ADF,你知道DE与BF是否平行吗?试说明理由.
5、如图,一束平行光线AB与DE射向一个水平镜面后被反射,此时
∠l=∠2,∠3=∠4.
(1)∠1与∠3的大小有什么关系?∠2与∠4呢?
(2)反射光线BC与EF也平行吗?
课后作业答案:
1、A
2、∠4=75°.
3、(1)因为∠1=∠2,所以BF∥CE,根据是:内错角相等,两直线平行.
(2)因为∠1=∠M,所以AM∥CE.根据是:内错角相等,两直线平行.
(3)因为∠1=∠C,所以AC∥MD,根据是:同位角相等,两直线平行.
(4)因为∠A+∠3=180°,所以AM∥BF,根据是:同旁内角互补,两直线平行.
4、DE∥BF,理由如下:
∵BF平分∠ABC,DE平分∠ADF,
∴,(角平分线定义).
∵DF∥BC,
∴∠ABC=∠ADF(两直线平行,同位角相等).
∴∠1=∠3(等量代换).
∴DE∥BF(同位角相等,两直线平行).
5、(1)因为AB∥DE,
所以∠1=∠3(两直线平行,同位角相等).
因为∠1=∠2,∠3=∠4,
所以∠2=∠4(等量代换).
(2)因为∠2=∠4,
所以BC∥EF(同位角相等,两直线平行).
b
1
2
a
c
4
A
C
B
D
1
2
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
