2018_2019学年高中数学第一章解三角形1.1正弦定理和余弦定理第2课时余弦定理课件新人教A版必修5(35张PPT)
文档属性
| 名称 | 2018_2019学年高中数学第一章解三角形1.1正弦定理和余弦定理第2课时余弦定理课件新人教A版必修5(35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-25 20:23:44 | ||
图片预览








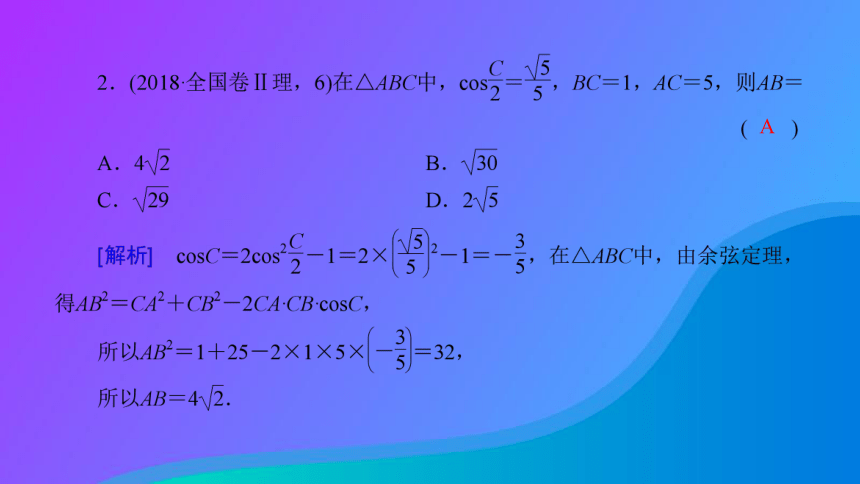



文档简介
课件35张PPT。第 一 章解三角形1.1 正弦定理和余弦定理第2课时 余弦定理自主预习学案中国海监船肩负着我国海域的维权、执法使命.某时某中国海监船位于中国南海的A处,与我国海岛B相距s n mile.据观测得知有一外国探油船位于我国海域C处进行非法资源勘探,这艘中国海监船奉命以v n mile/小时的速度前去驱逐.假如能测得∠BAC=α,BC=m n mile,你能根据上述数据计算出它赶到C处的时间吗?
减去 两 a2+b2-2abcosC 2.利用余弦定理及其推论解三角形的类型
(1)已知三角形的__________求三个角;
(2)已知三角形的________________求第三边及两角.
3.余弦定理和勾股定理的关系
在△ABC中,由余弦定理得c2=a2+b2-2abcosC,若角C=90°,则cosC=0,于是c2=a2+b2,这说明勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.
设c是△ABC中最大的边(或C是△ABC中最大的角),则
a2+b2a2+b2=c2?△ABC是________三角形,且角C为________;
a2+b2>c2?△ABC是________三角形,且角C为________. 三条边 两边及其夹角 钝角 钝角 直角 直角 锐角 锐角 C A
3.在△ABC中,已知a=5,b=7,c=8,则A+C= ( )
A.90° B.120°
C.135° D.150°B 4.(2018-2019学年度甘肃天水一中高二月考)在△ABC中,已知sinA∶sinB∶sinC=5∶7∶8,则∠B的大小为______.互动探究学案命题方向1 ?已知两边及一角解三角形例题 1[分析] 已知两边及其中一边的对角,先由余弦定理列方程求c,然后求A、C.『规律总结』 已知两边及一角解三角形的方法:
(1)当已知两边及它们的夹角时,用余弦定理求解出第三边,再用正弦定理和三角形内角和定理求解另外两角,只有一解;
(2)当已知两边及其一边的对角时,可用余弦定理建立一元二次方程,解方程求出第三边;也可用正弦定理求解,但都要注意解的情况的讨论.利用余弦定理求解相对简便.D
(2)已知△ABC中,a=1,b=1,C=120°,则边c=______.命题方向2 ?已知三边解三角形例题 2『规律总结』 已知三边解三角形的方法
(1)先利用余弦定理求出一个角的余弦,从而求出第一个角;再利用余弦定理或由求得的第一个角,利用正弦定理求出第二个角;最后利用三角形的内角和定理求出第三个角.
(2)利用余弦定理求三角的余弦,进而求得三个角.120° 命题方向3 ?判断三角形的形状 在△ABC中,若b2sin2C+c2sin2B=2bccosBcosC,试判断△ABC的形状.
[分析] 思路一,利用正弦定理将已知等式化为角的关系;思路二,利用余弦定理将已知等式化为边的关系.例题 3『规律总结』 已知三角形的边或角的关系式解三角形或判断三角形的形状,可先观察条件式的特点,再依据此特点选取变形方法,当等式两端各项都含有边时常用正弦定理变形,当等式两边含有角的正弦的同次幂时,常用正弦定理变形,当含有边的积式及边的平方和与差的形式时,常考虑用余弦定理变形,可以化边为角,通过三角变换求解,也可以化角为边,通过因式分解、配方等方法得出边的关系等等. 在钝角三角形ABC中,a=1,b=2,c=t,且C是最大角,求t的取值范围.例题 4忽略三角形的条件致错 [辨析] 错解中忽略了三角形中,两边之和大于第三边而导致错误.例题 5正弦、余弦定理的综合应用 [分析] (1)已知等式2cosC(acosB+bcosA)=C中有角有边,且等式两边边长的次数相同,结合括号内式子的特点联想到两角和的正弦公式,故化边为角,结合内角和定理及诱导公式求解;
(2)已知边c,角C和三角形面积,利用面积公式可求得a、b关系,只要求出a+b即可.C A 1
减去 两 a2+b2-2abcosC 2.利用余弦定理及其推论解三角形的类型
(1)已知三角形的__________求三个角;
(2)已知三角形的________________求第三边及两角.
3.余弦定理和勾股定理的关系
在△ABC中,由余弦定理得c2=a2+b2-2abcosC,若角C=90°,则cosC=0,于是c2=a2+b2,这说明勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.
设c是△ABC中最大的边(或C是△ABC中最大的角),则
a2+b2
a2+b2>c2?△ABC是________三角形,且角C为________. 三条边 两边及其夹角 钝角 钝角 直角 直角 锐角 锐角 C A
3.在△ABC中,已知a=5,b=7,c=8,则A+C= ( )
A.90° B.120°
C.135° D.150°B 4.(2018-2019学年度甘肃天水一中高二月考)在△ABC中,已知sinA∶sinB∶sinC=5∶7∶8,则∠B的大小为______.互动探究学案命题方向1 ?已知两边及一角解三角形例题 1[分析] 已知两边及其中一边的对角,先由余弦定理列方程求c,然后求A、C.『规律总结』 已知两边及一角解三角形的方法:
(1)当已知两边及它们的夹角时,用余弦定理求解出第三边,再用正弦定理和三角形内角和定理求解另外两角,只有一解;
(2)当已知两边及其一边的对角时,可用余弦定理建立一元二次方程,解方程求出第三边;也可用正弦定理求解,但都要注意解的情况的讨论.利用余弦定理求解相对简便.D
(2)已知△ABC中,a=1,b=1,C=120°,则边c=______.命题方向2 ?已知三边解三角形例题 2『规律总结』 已知三边解三角形的方法
(1)先利用余弦定理求出一个角的余弦,从而求出第一个角;再利用余弦定理或由求得的第一个角,利用正弦定理求出第二个角;最后利用三角形的内角和定理求出第三个角.
(2)利用余弦定理求三角的余弦,进而求得三个角.120° 命题方向3 ?判断三角形的形状 在△ABC中,若b2sin2C+c2sin2B=2bccosBcosC,试判断△ABC的形状.
[分析] 思路一,利用正弦定理将已知等式化为角的关系;思路二,利用余弦定理将已知等式化为边的关系.例题 3『规律总结』 已知三角形的边或角的关系式解三角形或判断三角形的形状,可先观察条件式的特点,再依据此特点选取变形方法,当等式两端各项都含有边时常用正弦定理变形,当等式两边含有角的正弦的同次幂时,常用正弦定理变形,当含有边的积式及边的平方和与差的形式时,常考虑用余弦定理变形,可以化边为角,通过三角变换求解,也可以化角为边,通过因式分解、配方等方法得出边的关系等等. 在钝角三角形ABC中,a=1,b=2,c=t,且C是最大角,求t的取值范围.例题 4忽略三角形的条件致错 [辨析] 错解中忽略了三角形中,两边之和大于第三边而导致错误.例题 5正弦、余弦定理的综合应用 [分析] (1)已知等式2cosC(acosB+bcosA)=C中有角有边,且等式两边边长的次数相同,结合括号内式子的特点联想到两角和的正弦公式,故化边为角,结合内角和定理及诱导公式求解;
(2)已知边c,角C和三角形面积,利用面积公式可求得a、b关系,只要求出a+b即可.C A 1
