2018_2019学年高中数学第一章解三角形 正弦定理和余弦定理第3课时正余弦定理的综合应用课件新人教A版必修5(48张PPT)
文档属性
| 名称 | 2018_2019学年高中数学第一章解三角形 正弦定理和余弦定理第3课时正余弦定理的综合应用课件新人教A版必修5(48张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-25 20:28:13 | ||
图片预览









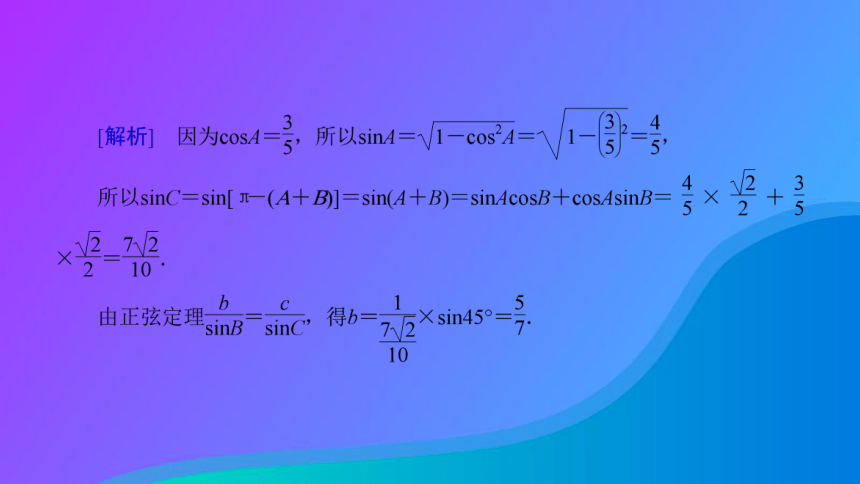

文档简介
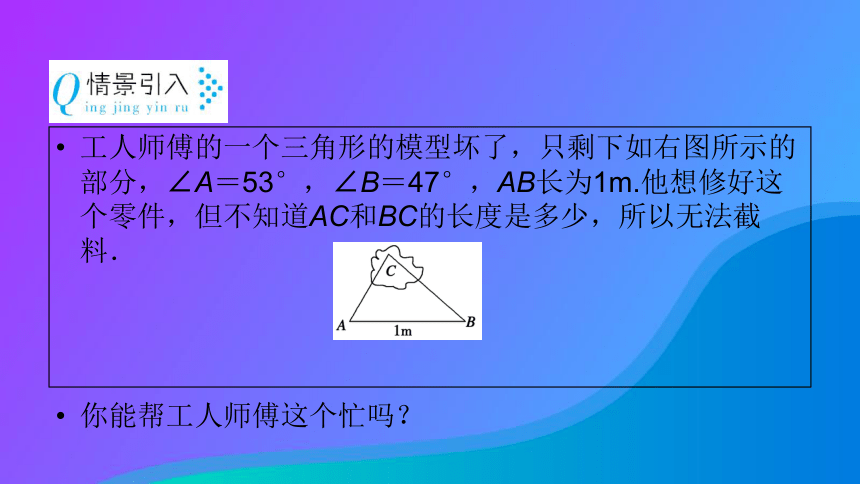
课件48张PPT。第 一 章解三角形1.1 正弦定理和余弦定理第3课时 正、余弦定理的综合应用自主预习学案工人师傅的一个三角形的模型坏了,只剩下如右图所示的部分,∠A=53°,∠B=47°,AB长为1m.他想修好这个零件,但不知道AC和BC的长度是多少,所以无法截料.
你能帮工人师傅这个忙吗?1.(1)正弦定理的数学表达式为____________________.
(2)余弦定理的数学表达式为_____________________________、________________________、_________________________.
2.应用正弦定理可以解决怎样的解三角形问题?
(1)__________________________________________.
(2)______________________________________________.a2=b2+c2-2bccosA b2=a2+c2-2accosB c2=a2+b2-2abcosC 已知三角形的任意两个角与一边,解三角形 已知三角形的两边与其中一边的对角,解三角形
3.应用余弦定理可以解决怎样的解三角形问题?
(1)______________________________________.
(2)______________________________.
4.三角形的面积公式
由正弦定理可得三角形的面积S=__________=__________=_________.已知三角形的两边及其夹角,解三角形 已知三角形的三边,解三角形 B C B B 等腰直角三角形 互动探究学案命题方向1 ?综合应用正弦、余弦定理求边和角例题 1[分析] 正确挖掘图形中的几何条件,搞清在哪个三角形中利用正、余弦定理求解.『规律总结』 正、余弦定理都是用来解三角形的,但在解题过程中要有意识地考虑用哪个定理更适合,或是两个定理都要用,应抓住两个定理的特点:正弦定理“边对角”,余弦定理“边夹角”,正确选择定理是解决此类题目的关键.命题方向2 ?三角形的面积公式例题 2
命题方向3 ?正、余弦定理与三角恒等变换的综合应用 在△ABC中,角A、B、C的对边分别为a、b、c,且bcosC=3acosB-ccosB.
(1)求cosB的值;例题 3『规律总结』 解三角形的综合应用问题常见的有:
(1)正、余弦定理和三角变换相结合,一般先进行边角互化,再利用三角公式变形,然后求角、求值或证明三角恒等式、判断三角形的形状等.
(2)三角形与平面向量结合命题,先利用向量的平行、垂直等条件脱去向量外衣,转化为纯三角函数问题.然后依据三角公式和解三角形知识求解. 在△ABC中,角A、B、C满足2B=A+C,B的对边b=1,求a+c的取值范围.例题 4与三角形有关的求最值或取值范围问题,先利用正、余弦定理理清三角形中量的关系,再将求最值或取值范围的量表达为某一变量的函数,转化为函数值域或最值问题.求取值范围问题 在锐角△ABC中,a=2bsinA,试求cosA+sinC的取值范围.
[分析] 由a=2bsinA运用正弦定理求得B,再利用三角形内角和定理将cosA+sinC转化为关于A(或C)的三角函数,再求三角函数的取值范围.例题 5B D [解析] 由余弦定理,得b2=a2+c2-2accosB,
∴49=a2+25-5a,
∴a2-5a-24=0
∴a=8或a=-3(舍去),∴a=8.2 4.在△ABC中,若A=120°,AB=5,BC=7,则AC=_____.3
你能帮工人师傅这个忙吗?1.(1)正弦定理的数学表达式为____________________.
(2)余弦定理的数学表达式为_____________________________、________________________、_________________________.
2.应用正弦定理可以解决怎样的解三角形问题?
(1)__________________________________________.
(2)______________________________________________.a2=b2+c2-2bccosA b2=a2+c2-2accosB c2=a2+b2-2abcosC 已知三角形的任意两个角与一边,解三角形 已知三角形的两边与其中一边的对角,解三角形
3.应用余弦定理可以解决怎样的解三角形问题?
(1)______________________________________.
(2)______________________________.
4.三角形的面积公式
由正弦定理可得三角形的面积S=__________=__________=_________.已知三角形的两边及其夹角,解三角形 已知三角形的三边,解三角形 B C B B 等腰直角三角形 互动探究学案命题方向1 ?综合应用正弦、余弦定理求边和角例题 1[分析] 正确挖掘图形中的几何条件,搞清在哪个三角形中利用正、余弦定理求解.『规律总结』 正、余弦定理都是用来解三角形的,但在解题过程中要有意识地考虑用哪个定理更适合,或是两个定理都要用,应抓住两个定理的特点:正弦定理“边对角”,余弦定理“边夹角”,正确选择定理是解决此类题目的关键.命题方向2 ?三角形的面积公式例题 2
命题方向3 ?正、余弦定理与三角恒等变换的综合应用 在△ABC中,角A、B、C的对边分别为a、b、c,且bcosC=3acosB-ccosB.
(1)求cosB的值;例题 3『规律总结』 解三角形的综合应用问题常见的有:
(1)正、余弦定理和三角变换相结合,一般先进行边角互化,再利用三角公式变形,然后求角、求值或证明三角恒等式、判断三角形的形状等.
(2)三角形与平面向量结合命题,先利用向量的平行、垂直等条件脱去向量外衣,转化为纯三角函数问题.然后依据三角公式和解三角形知识求解. 在△ABC中,角A、B、C满足2B=A+C,B的对边b=1,求a+c的取值范围.例题 4与三角形有关的求最值或取值范围问题,先利用正、余弦定理理清三角形中量的关系,再将求最值或取值范围的量表达为某一变量的函数,转化为函数值域或最值问题.求取值范围问题 在锐角△ABC中,a=2bsinA,试求cosA+sinC的取值范围.
[分析] 由a=2bsinA运用正弦定理求得B,再利用三角形内角和定理将cosA+sinC转化为关于A(或C)的三角函数,再求三角函数的取值范围.例题 5B D [解析] 由余弦定理,得b2=a2+c2-2accosB,
∴49=a2+25-5a,
∴a2-5a-24=0
∴a=8或a=-3(舍去),∴a=8.2 4.在△ABC中,若A=120°,AB=5,BC=7,则AC=_____.3
