高中数学第一章统计1.7相关性课件北师大版必修3(17张PPT)
文档属性
| 名称 | 高中数学第一章统计1.7相关性课件北师大版必修3(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 315.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-25 00:00:00 | ||
图片预览






文档简介
课件17张PPT。第一章 统计第七节 相关性 学习目标了解函数关系与相关关系的不同,通过收集现实问题中两个变量的数据作出散点图,能利用散点图直观认识变量间的相关关系。
经历用不同的估算方法来描述两个变量线性相关的过程,体会研究两个变量间依赖关系的一般方法。
通过利用散点图直观认识变量间的相关关系,并能用普遍联系的观点思考和解决生活中的数学现象,进一步增强创新意识,提高创新能力。
学习重点
相关关系的概念,画出给定变量间的散点图
学习难点
寻求两个变量间线性相关关系的直线方程。“相关”的由来英国人类学家盖尔顿首次在《自然遗传》一书中,提出并阐明了“相关”和“相关系数”两个概念,为相关论奠定了基础。其后,他和英国统计学家皮尔逊对上千个家庭的身高、臂长、一拃长做了测量。
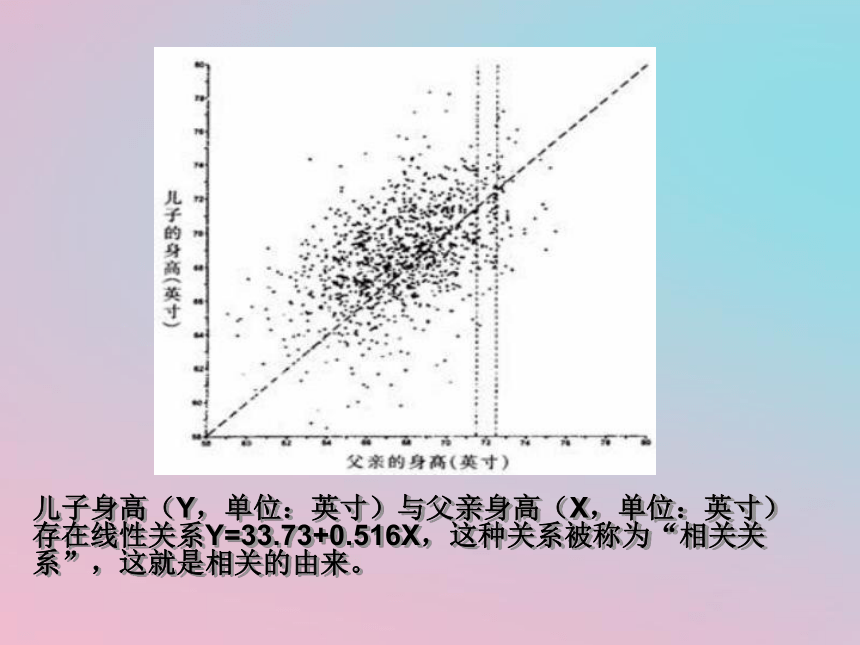
为研究父亲与成年儿子身高之间的关系,皮尔逊测量了1078对父子的身高。他把1078对数字表示在坐标上,形成了下面的图形(X轴上的数代表父亲身高,Y轴上的数代表儿子的身高):
儿子身高(Y,单位:英寸)与父亲身高(X,单位:英寸)存在线性关系Y=33.73+0.516X,这种关系被称为“相关关系”,这就是相关的由来。问题提出 问题1:正方形的面积y与边长x之间具有什么样的关系?
问题2:某水田水稻产量y与施肥量x之间是否有一个确定性的关系?问题3:人的身高与体重之间有确定性的关系吗?为了了解人的身高与体重的关系,随机地抽取9名15岁的男生,测得如下数据:抽象概括散点图
再考虑两个量的关系时,为了对变量之间的关系有一个大致的了解,人们通常将变量所对应的点描出来,这些点就组成了变量之间的一个图,通常称这种图为变量之间的散点图xxxOOOyyy散点图曲线拟合:
从散点图上可以看出,如果变量之间存在某种关系,这些点会有一个集中的大趋势,这种趋势通常可以用一条光滑的曲线来近似,这样近似的过程成为曲线拟合。
线性相关
若两个变量x和y的散点图中,所有点看上去都在一条直线附近波动,则称变量间是线性相关的。
非线性相关
若所有点看上去都在某条曲线(不是一条直线)附近波动,则称此相关为非线性相关的。此时,可用一条曲线来拟合。
不相关
如果所有的点在散点图中没有显示任何关系,则称变量间是不相关的。
探究1、下列变量中具有相关关系的是( )
A、正方形的面积与边长
B、匀速行驶的车辆的行驶距离与时间
C、人的身高与体重
D、人的身高与视力
探究2、根据下面的数据判断它们是否有相关关系思考 : 生活中还有那些量具有相关关系呢?例题分析例 一般说来,一个人的身材越高,他的手就越大,相应地,他的右手一拃长就越长,因此,人 的身高与右手一拃长之间存在着一定的关系 。为了对这个问题进行调查,我们下面收集咱们班50名同学的身高与右手一拃长的数据。活动一请同学们开始测量自己的右手
一拃长。
活动二
请各组组长收集本组同学的
有关数据,并填入上表。活动三
请同学们根据表中的数据,制成散点图(以小组为单位进行散点图的绘制)如果近似成线性关系,请画出一条直线来近似地表示这种线性关系。请与同学交流。
如果一个学生的身高是188cm.你能估计他的右手一拃长大概有多长吗?
你能从散点图中发现身高与右手一拃长之间的 近拟关系吗?问题
不同的求拟合曲线的方法各有什么样的优点与缺点?你对同学不同的求解方法有什么样的理解与认识?
你能改进他们的求解方法吗?议一议:某小卖部6天卖出热茶的杯数(y)与当天气温(x) 的数据如表:
(1)根据表中提供的数据画出散点图。
(2)你能从散点图中看出,气温与卖出的热茶杯数近似成什么关系吗?
(3)如果近似成线性关系,请画出一条直线来近似表示这种线性关系。
(4)如果某天气温是-5,请预测大约能卖出热茶多少杯?
做一做:谢谢学习
经历用不同的估算方法来描述两个变量线性相关的过程,体会研究两个变量间依赖关系的一般方法。
通过利用散点图直观认识变量间的相关关系,并能用普遍联系的观点思考和解决生活中的数学现象,进一步增强创新意识,提高创新能力。
学习重点
相关关系的概念,画出给定变量间的散点图
学习难点
寻求两个变量间线性相关关系的直线方程。“相关”的由来英国人类学家盖尔顿首次在《自然遗传》一书中,提出并阐明了“相关”和“相关系数”两个概念,为相关论奠定了基础。其后,他和英国统计学家皮尔逊对上千个家庭的身高、臂长、一拃长做了测量。
为研究父亲与成年儿子身高之间的关系,皮尔逊测量了1078对父子的身高。他把1078对数字表示在坐标上,形成了下面的图形(X轴上的数代表父亲身高,Y轴上的数代表儿子的身高):
儿子身高(Y,单位:英寸)与父亲身高(X,单位:英寸)存在线性关系Y=33.73+0.516X,这种关系被称为“相关关系”,这就是相关的由来。问题提出 问题1:正方形的面积y与边长x之间具有什么样的关系?
问题2:某水田水稻产量y与施肥量x之间是否有一个确定性的关系?问题3:人的身高与体重之间有确定性的关系吗?为了了解人的身高与体重的关系,随机地抽取9名15岁的男生,测得如下数据:抽象概括散点图
再考虑两个量的关系时,为了对变量之间的关系有一个大致的了解,人们通常将变量所对应的点描出来,这些点就组成了变量之间的一个图,通常称这种图为变量之间的散点图xxxOOOyyy散点图曲线拟合:
从散点图上可以看出,如果变量之间存在某种关系,这些点会有一个集中的大趋势,这种趋势通常可以用一条光滑的曲线来近似,这样近似的过程成为曲线拟合。
线性相关
若两个变量x和y的散点图中,所有点看上去都在一条直线附近波动,则称变量间是线性相关的。
非线性相关
若所有点看上去都在某条曲线(不是一条直线)附近波动,则称此相关为非线性相关的。此时,可用一条曲线来拟合。
不相关
如果所有的点在散点图中没有显示任何关系,则称变量间是不相关的。
探究1、下列变量中具有相关关系的是( )
A、正方形的面积与边长
B、匀速行驶的车辆的行驶距离与时间
C、人的身高与体重
D、人的身高与视力
探究2、根据下面的数据判断它们是否有相关关系思考 : 生活中还有那些量具有相关关系呢?例题分析例 一般说来,一个人的身材越高,他的手就越大,相应地,他的右手一拃长就越长,因此,人 的身高与右手一拃长之间存在着一定的关系 。为了对这个问题进行调查,我们下面收集咱们班50名同学的身高与右手一拃长的数据。活动一请同学们开始测量自己的右手
一拃长。
活动二
请各组组长收集本组同学的
有关数据,并填入上表。活动三
请同学们根据表中的数据,制成散点图(以小组为单位进行散点图的绘制)如果近似成线性关系,请画出一条直线来近似地表示这种线性关系。请与同学交流。
如果一个学生的身高是188cm.你能估计他的右手一拃长大概有多长吗?
你能从散点图中发现身高与右手一拃长之间的 近拟关系吗?问题
不同的求拟合曲线的方法各有什么样的优点与缺点?你对同学不同的求解方法有什么样的理解与认识?
你能改进他们的求解方法吗?议一议:某小卖部6天卖出热茶的杯数(y)与当天气温(x) 的数据如表:
(1)根据表中提供的数据画出散点图。
(2)你能从散点图中看出,气温与卖出的热茶杯数近似成什么关系吗?
(3)如果近似成线性关系,请画出一条直线来近似表示这种线性关系。
(4)如果某天气温是-5,请预测大约能卖出热茶多少杯?
做一做:谢谢学习
