3.5 力的正交分解法总结 27张PPT
文档属性
| 名称 | 3.5 力的正交分解法总结 27张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 214.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-03-25 21:34:26 | ||
图片预览



文档简介
正交分解法
多个力的合力是唯一的
力的合成和分解
一个力的分解是不确定的
分解与合成的原则
三角形法
等效原则
平行四边形法则
F
F
F1
F2
F1
F2
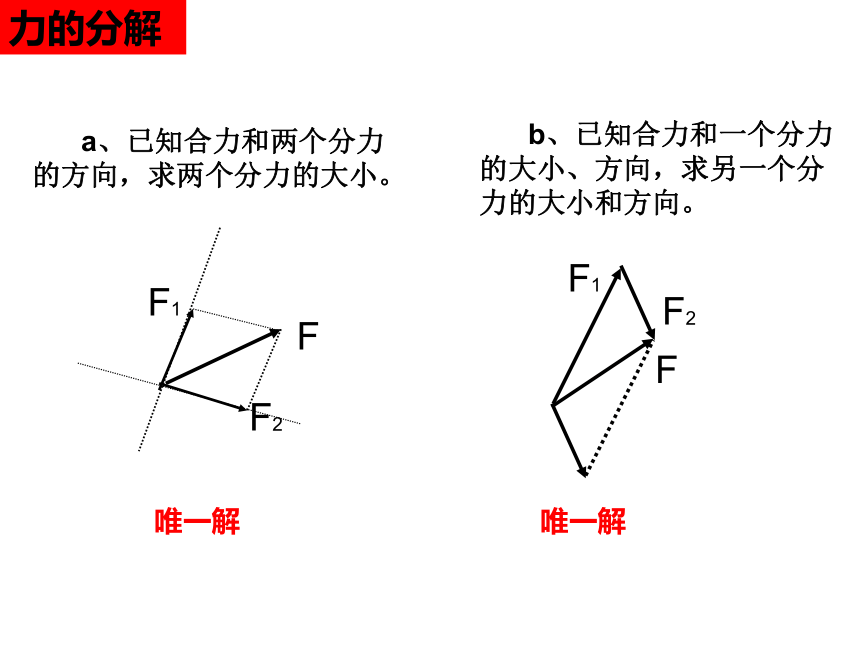
a、已知合力和两个分力的方向,求两个分力的大小。
唯一解
b、已知合力和一个分力的大小、方向,求另一个分力的大小和方向。
唯一解
力的分解
F2
F1
F1
F2
F
θ
F
θ
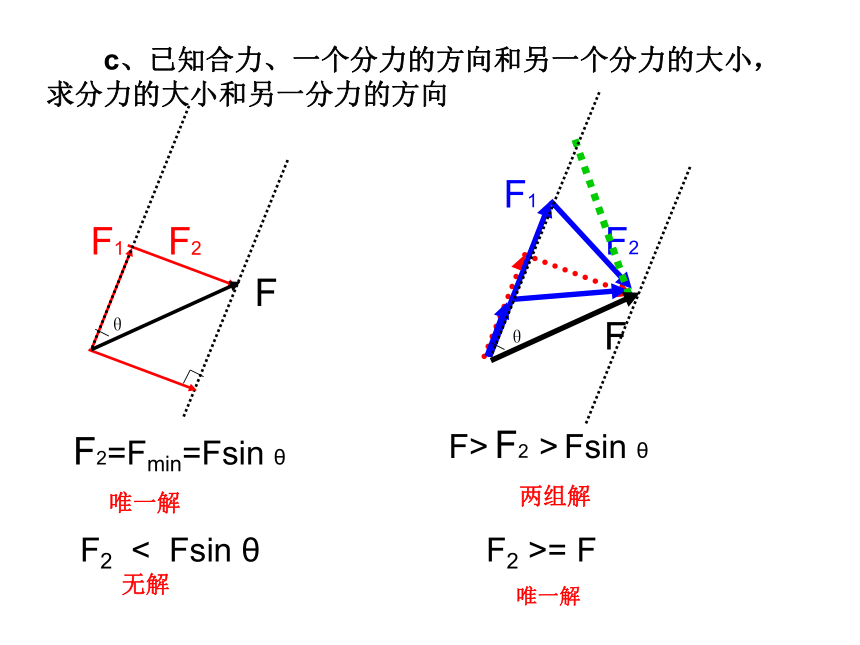
c、已知合力、一个分力的方向和另一个分力的大小,求分力的大小和另一分力的方向
F2=Fmin=Fsin θ
唯一解
F> F2 > Fsin θ
两组解
F2 < Fsin θ
无解
F2 >= F
唯一解
F1
F2
F3
F4
F12
F123
F1234
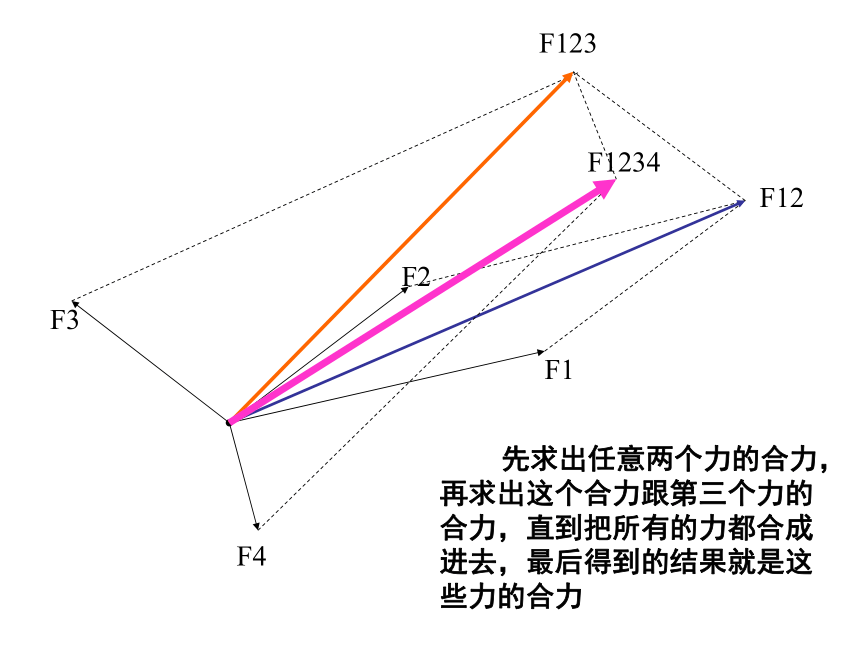
先求出任意两个力的合力,再求出这个合力跟第三个力的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力
求合力的基本方法有作图法和计算法。
正交分解法
正交分解法的优点:
作图法原理简单易掌握,但结果误差较大。
定量计算多个共点力的合力时,如果连续运用平行四边
形定则求解,一般需要解多个任意三角形,一次接一次地求
部分合力的大小和方向,计算十分麻烦。而用正交分解法求
合力就显得十分简明方便。
正交分解法求合力,运用了“欲合先分”的策略,降低了
运算的难度,是解题中的一种重要思想方法。
F
x
y
O
Fy
Fx
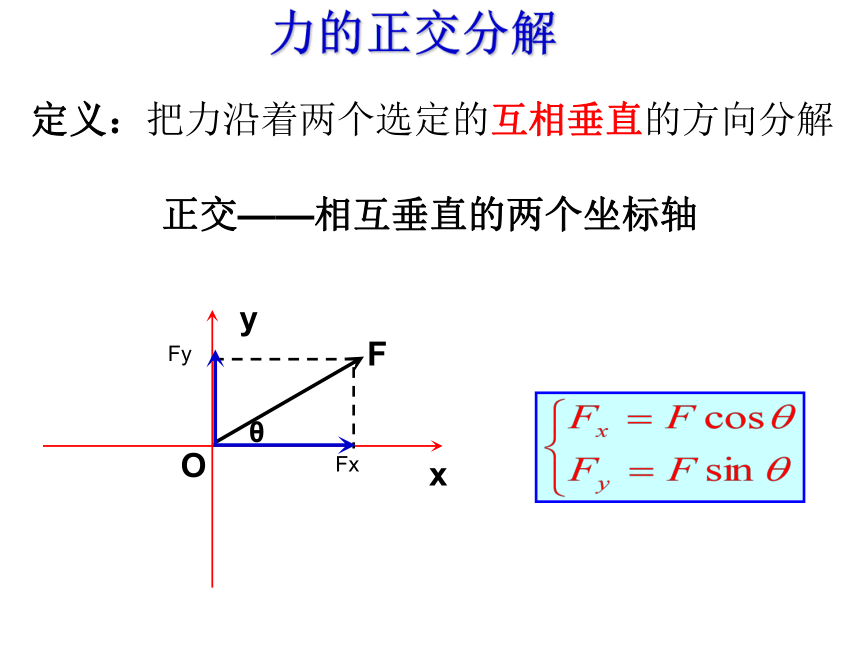
力的正交分解
θ
定义:把力沿着两个选定的互相垂直的方向分解
正交——相互垂直的两个坐标轴
F1
F2
F3
x
y
O
F2y
F1y
F3y
F3x
F1x
F2X
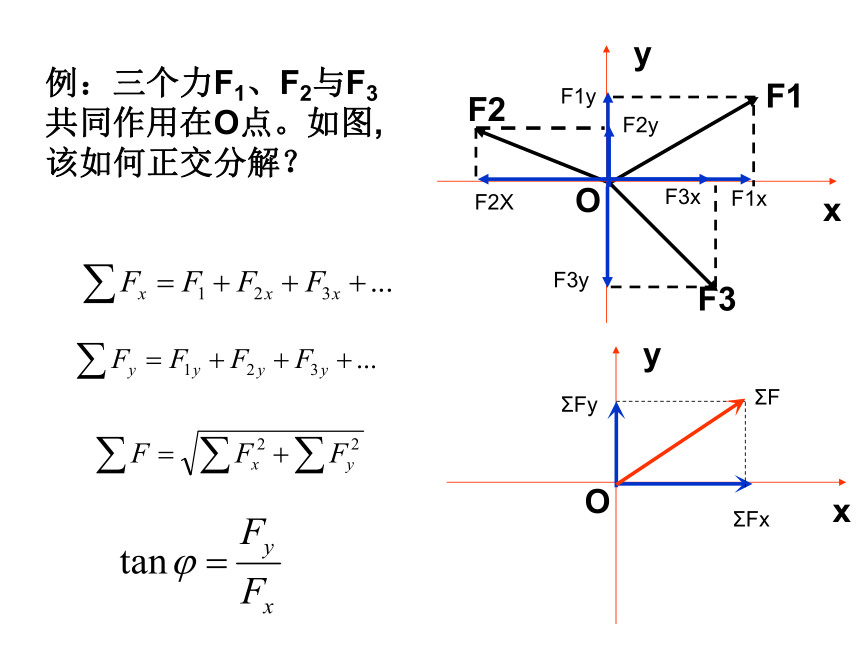
例:三个力F1、F2与F3共同作用在O点。如图, 该如何正交分解?
x
y
O
ΣFx
ΣFy
ΣF
G
F1
F2
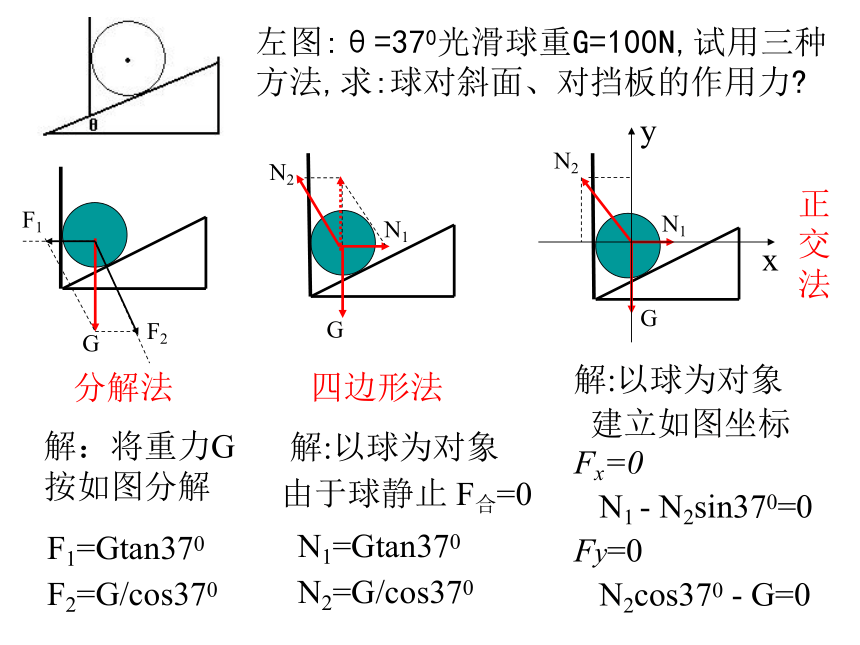
解:将重力G按如图分解
F1=Gtan370
F2=G/cos370
G
N1
N2
解:以球为对象
由于球静止 F合=0
N1=Gtan370
N2=G/cos370
解:以球为对象
建立如图坐标
Fx=0
N1 - N2sin370=0
Fy=0
N2cos370 - G=0
x
y
N1
N2
G
左图:θ=370光滑球重G=100N,试用三种方法,求:球对斜面、对挡板的作用力?
分解法
四边形法
正交法
目的:
基本思想:
正交分解法求合力,运用了“欲合先分”的策略,即为了合成而分解,降低了运算的难度,是一种重要思想方法。
是化复杂的矢量运算为普通的代数运算,将力的合成化简为同向或反向或垂直方向。便于运用普通代数运算公式来解决矢量的运算。
2、以力的作用点为坐标原点,恰当地建立直角坐标系,标出x轴和y轴。
步骤
3、将不在坐标轴上的各力分解为沿两坐标轴方向 的分力,并在图上标明。
4、将坐标轴上的力分别合成,按坐标轴规定的方向求代数和
即:Fx合=F1x+F2x+F3x+......?
?????? Fy合=F1y+F2y+F3y+......??
5、最后求再求合力F的大小和方向
1、先对物体进行受力分析,画出受力示意图。
注意:坐标轴方向的选择虽具有任意性,
但原则是:使坐标轴与尽量多的力重合,
使需要分解的力尽量少和容易分解。
例1:一个物体受到四个力的作用,已知F1=1N,方向正东;F2=2N,方向东偏北600,F3= N,方向西偏北300;F4=4N,方向东偏南600,求物体所受的合力。
F1
F2
F3
F4
x
y
F2x
F2y
F3y
F3x
F4x
F4y
600
300
600
F1
F2
F3
F4
x
y
F2x
F2y
F3y
F3x
F4x
F4y
600
300
600
Fy= N
Fx = -1/2 N
F =1N
x
y
例3 有五个力作用于一点O,这五个力构成一个正六边形的两邻边和三条对角线,如图所示,设F3=10N,则五个力的合力大小为多少?
正交分解
X轴: F1X=F5X=2.5N F2X=F4X=7.5N F3X=10N
Y轴: F1Y+F5Y=0 F2Y+F4Y=0 F3Y=0
F1X+F2X+F3X+F4X+F5X=30N
F1Y+F2Y+F3Y+F4Y+F5Y=0
F=30N
Y
X
把所有的力放在一个直角坐标系内沿轴方向分解,根据“同向相加,异向相减”的原则分别得出两坐标轴方向上的合力. 最后 (如果需要) ,再对两坐标轴上得出的合力进行合成得到最终的合力.
正交分解法则
Fx合=Fx-f= G ?sin?-f
Fy合=N-Fy= N-G?cos?
f
N
G
x
y
?
建立坐标轴x轴和y轴时应使尽量多的力落在坐标轴上,减少分解.
小窍门1
F合=
Fx合2+Fy合2
?
G
F
N
f
?
Fx合=Fx-f= F?cos?-f
Fy合=Fy+N-G= F?sin?+N-G.
F
?
放置在水平地面上的物块,受到一个与水平面夹角为?的力F.对物块受到的力进行正交分解.
Fx
Fy
F合=
Fx合2+Fy合2
解:木块受力分析如图所示以水平方向和竖直方向为x轴和y轴,将F分解在这两个方向上.则有:
小窍门2
------常见的物体情景的正交分解
1.斜面
------常将平行于斜面方向和垂直于斜面方向作为x轴和y轴,然后将其它力都分解在这两个方向上.
2.水平面(或竖直面),但可能存在与水平面(或竖直面)成一定夹角的力.
------常将水平面和竖直面作为x轴和y轴,然后将其它力都分解在这两个方向上.
f
N
G
x
y
?
解:木块受力分析如图所示以平行于斜面方向和垂直于斜面方向为x轴和y轴,将重力分解在这两个方向.则有:
F x合=Gx-f=G ?sin? - f
F y合=N- Gy= N - G ?cos?
一物块放置在斜面上,斜面和物块都静止.斜面的倾角为?,斜面质量为M,物块质量为m, 斜面与地面之间无摩擦.请画出物块和斜面的受力示意图,并对它们受到的力分别进行正交分解.
Gx
Gy
以水平方向和竖直方向为x轴和y轴,将木块对斜面的压力及木块与斜面之间的摩擦力分解在这两个方向上.则有:
F’x合=fx-N’x=fcos? - N’sin?
F’y合= N1-N’y-G-fy=N1 - fsin? - N’cos? - G1
解:斜面的受力情况如左图所示.
f
N’
G1
N1
x
y
一物块放置在斜面上,斜面和物块都静止.斜面的倾角为?,斜面质量为M,物块质量为m, 斜面与地面之间无摩擦.请画出物块和斜面的受力示意图,并对它们受到的力分别进行正交分解.
------正交分解法解决平衡问题
当运用正交分解法把所有的力放在一个直角坐标系内时,x轴上的合力和y轴上的合力均为0.
小窍门3
利用正交分解法解题的的一般步骤:
1、分析物体 的受力情况;
2、建立直角坐标系;
3、根据物体沿x轴或y轴的所处的状态列方程求解。
建立原则:
a、沿物体的运动方向和垂直于物体的运动方向;
b、沿力的方向,使尽量多的力在坐标轴上。
Gsin300 - f - Fcos300=0 N + Fsin300 - Gcos300=0
f
N
G
F
y
x
30°
f
N
G
F
30°
例:一物块在拉力F的作用下静止在倾角为30 °的斜面上,物块重40N, 拉力F与斜面成30°角,大小为10N.求物块所受支持力和摩擦力的大小.
F=10N
f = Gsin300 - Fcos300=[40× -10× ]N=11.34N
1
2
3
2
N=Gcos300-Fsin300=[40 × - 10 × ]N=29.64N
1
2
3
2
一物体放在水平桌面上,现对物体施加一个斜向上的拉力F,使物体在水平桌面上做匀速直线运动.下面说法正确的是:
A.物体不一定受摩擦力作用
B.物体所受的滑动摩擦力与F的合外力一定为0
C.物体所受的滑动摩擦力与F的合外力一定向前
D.物体所受的滑动摩擦力与F的合外力一定向上
物体运动方向
如图,重为G的光滑小球用细绳悬挂在墙壁上的O点,细绳与竖直方面的夹角为?.小球对细绳的拉力及对墙壁的压力有多大?如果加大细绳的长度,使悬挂点由O点上移到O’,小球对墙壁的压力和对细绳的拉力如何变化?
O
O’
O
O’
G
N
F
x
y
当将绳子加长,悬挂点上移到O’时, ?减小
因此,绳子拉力F减小,N减小
小球对绳子的拉力大小等于F,对墙壁的压力大小等于N.因此,变化情况同F和N一样.
N - Fsin? =0 Fcos? - G=0
F =G/ cos? N = Fsin? = Gtan?
如图,重为G的物块放置在倾角为?的斜面上,在水平外力F的作用下保持静止状态.若将水平外力增大一些(物块仍静止),则有:
A.物块所受摩擦力一定增大
B.物块所受摩擦力一定减小
C.物块所受最大静摩擦力一定增大
D.以上都不对
F
F
N
G
x
y
当Gsin?> Fcos?时,静摩擦力f方向应该沿斜面向上,大小为(Gsin? - Fcos?).
当Gsin?< Fcos?时,静摩擦力f方向应该沿斜面向下,大小为(Fcos? - Gsin?).
因此,当F增大时,f可能增大也可能减小.
在y轴有:
N - Gcos? - Fsin?=0
因此,N= Gcos? + Fsin?
当F增大时,压力N增大.因此,最大静摩擦力增大.
总结
力学相关计算题解题一般步骤:
1.对物体进行受力分析.
2.建立直角坐标系,将力沿两个坐标轴分解.根据“同向相加,异向相减”的原则分别得出两坐标轴方向上的合力.
3.根据物体的状态得出各坐标轴上合力的值.如果物体处于平衡状态,则两个坐标轴上的合力都为0.
4.根据列出的关系式求解未知量.
在上面的例题中,如果斜面重100N,求地面对斜面的支持力(假设地面与斜面间无摩擦).
以水平方向和竖直方向为x轴和y轴,将木块对斜面的压力及木块与斜面之间的摩擦力分解在这两个方向上.
X轴:fcos? - N’sin? =0
y轴: N - fsin? - N’cos? - G= 0
N = fsin? + N’cos? + G
f
N’
G
N
x
y
?
多个力的合力是唯一的
力的合成和分解
一个力的分解是不确定的
分解与合成的原则
三角形法
等效原则
平行四边形法则
F
F
F1
F2
F1
F2
a、已知合力和两个分力的方向,求两个分力的大小。
唯一解
b、已知合力和一个分力的大小、方向,求另一个分力的大小和方向。
唯一解
力的分解
F2
F1
F1
F2
F
θ
F
θ
c、已知合力、一个分力的方向和另一个分力的大小,求分力的大小和另一分力的方向
F2=Fmin=Fsin θ
唯一解
F> F2 > Fsin θ
两组解
F2 < Fsin θ
无解
F2 >= F
唯一解
F1
F2
F3
F4
F12
F123
F1234
先求出任意两个力的合力,再求出这个合力跟第三个力的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力
求合力的基本方法有作图法和计算法。
正交分解法
正交分解法的优点:
作图法原理简单易掌握,但结果误差较大。
定量计算多个共点力的合力时,如果连续运用平行四边
形定则求解,一般需要解多个任意三角形,一次接一次地求
部分合力的大小和方向,计算十分麻烦。而用正交分解法求
合力就显得十分简明方便。
正交分解法求合力,运用了“欲合先分”的策略,降低了
运算的难度,是解题中的一种重要思想方法。
F
x
y
O
Fy
Fx
力的正交分解
θ
定义:把力沿着两个选定的互相垂直的方向分解
正交——相互垂直的两个坐标轴
F1
F2
F3
x
y
O
F2y
F1y
F3y
F3x
F1x
F2X
例:三个力F1、F2与F3共同作用在O点。如图, 该如何正交分解?
x
y
O
ΣFx
ΣFy
ΣF
G
F1
F2
解:将重力G按如图分解
F1=Gtan370
F2=G/cos370
G
N1
N2
解:以球为对象
由于球静止 F合=0
N1=Gtan370
N2=G/cos370
解:以球为对象
建立如图坐标
Fx=0
N1 - N2sin370=0
Fy=0
N2cos370 - G=0
x
y
N1
N2
G
左图:θ=370光滑球重G=100N,试用三种方法,求:球对斜面、对挡板的作用力?
分解法
四边形法
正交法
目的:
基本思想:
正交分解法求合力,运用了“欲合先分”的策略,即为了合成而分解,降低了运算的难度,是一种重要思想方法。
是化复杂的矢量运算为普通的代数运算,将力的合成化简为同向或反向或垂直方向。便于运用普通代数运算公式来解决矢量的运算。
2、以力的作用点为坐标原点,恰当地建立直角坐标系,标出x轴和y轴。
步骤
3、将不在坐标轴上的各力分解为沿两坐标轴方向 的分力,并在图上标明。
4、将坐标轴上的力分别合成,按坐标轴规定的方向求代数和
即:Fx合=F1x+F2x+F3x+......?
?????? Fy合=F1y+F2y+F3y+......??
5、最后求再求合力F的大小和方向
1、先对物体进行受力分析,画出受力示意图。
注意:坐标轴方向的选择虽具有任意性,
但原则是:使坐标轴与尽量多的力重合,
使需要分解的力尽量少和容易分解。
例1:一个物体受到四个力的作用,已知F1=1N,方向正东;F2=2N,方向东偏北600,F3= N,方向西偏北300;F4=4N,方向东偏南600,求物体所受的合力。
F1
F2
F3
F4
x
y
F2x
F2y
F3y
F3x
F4x
F4y
600
300
600
F1
F2
F3
F4
x
y
F2x
F2y
F3y
F3x
F4x
F4y
600
300
600
Fy= N
Fx = -1/2 N
F =1N
x
y
例3 有五个力作用于一点O,这五个力构成一个正六边形的两邻边和三条对角线,如图所示,设F3=10N,则五个力的合力大小为多少?
正交分解
X轴: F1X=F5X=2.5N F2X=F4X=7.5N F3X=10N
Y轴: F1Y+F5Y=0 F2Y+F4Y=0 F3Y=0
F1X+F2X+F3X+F4X+F5X=30N
F1Y+F2Y+F3Y+F4Y+F5Y=0
F=30N
Y
X
把所有的力放在一个直角坐标系内沿轴方向分解,根据“同向相加,异向相减”的原则分别得出两坐标轴方向上的合力. 最后 (如果需要) ,再对两坐标轴上得出的合力进行合成得到最终的合力.
正交分解法则
Fx合=Fx-f= G ?sin?-f
Fy合=N-Fy= N-G?cos?
f
N
G
x
y
?
建立坐标轴x轴和y轴时应使尽量多的力落在坐标轴上,减少分解.
小窍门1
F合=
Fx合2+Fy合2
?
G
F
N
f
?
Fx合=Fx-f= F?cos?-f
Fy合=Fy+N-G= F?sin?+N-G.
F
?
放置在水平地面上的物块,受到一个与水平面夹角为?的力F.对物块受到的力进行正交分解.
Fx
Fy
F合=
Fx合2+Fy合2
解:木块受力分析如图所示以水平方向和竖直方向为x轴和y轴,将F分解在这两个方向上.则有:
小窍门2
------常见的物体情景的正交分解
1.斜面
------常将平行于斜面方向和垂直于斜面方向作为x轴和y轴,然后将其它力都分解在这两个方向上.
2.水平面(或竖直面),但可能存在与水平面(或竖直面)成一定夹角的力.
------常将水平面和竖直面作为x轴和y轴,然后将其它力都分解在这两个方向上.
f
N
G
x
y
?
解:木块受力分析如图所示以平行于斜面方向和垂直于斜面方向为x轴和y轴,将重力分解在这两个方向.则有:
F x合=Gx-f=G ?sin? - f
F y合=N- Gy= N - G ?cos?
一物块放置在斜面上,斜面和物块都静止.斜面的倾角为?,斜面质量为M,物块质量为m, 斜面与地面之间无摩擦.请画出物块和斜面的受力示意图,并对它们受到的力分别进行正交分解.
Gx
Gy
以水平方向和竖直方向为x轴和y轴,将木块对斜面的压力及木块与斜面之间的摩擦力分解在这两个方向上.则有:
F’x合=fx-N’x=fcos? - N’sin?
F’y合= N1-N’y-G-fy=N1 - fsin? - N’cos? - G1
解:斜面的受力情况如左图所示.
f
N’
G1
N1
x
y
一物块放置在斜面上,斜面和物块都静止.斜面的倾角为?,斜面质量为M,物块质量为m, 斜面与地面之间无摩擦.请画出物块和斜面的受力示意图,并对它们受到的力分别进行正交分解.
------正交分解法解决平衡问题
当运用正交分解法把所有的力放在一个直角坐标系内时,x轴上的合力和y轴上的合力均为0.
小窍门3
利用正交分解法解题的的一般步骤:
1、分析物体 的受力情况;
2、建立直角坐标系;
3、根据物体沿x轴或y轴的所处的状态列方程求解。
建立原则:
a、沿物体的运动方向和垂直于物体的运动方向;
b、沿力的方向,使尽量多的力在坐标轴上。
Gsin300 - f - Fcos300=0 N + Fsin300 - Gcos300=0
f
N
G
F
y
x
30°
f
N
G
F
30°
例:一物块在拉力F的作用下静止在倾角为30 °的斜面上,物块重40N, 拉力F与斜面成30°角,大小为10N.求物块所受支持力和摩擦力的大小.
F=10N
f = Gsin300 - Fcos300=[40× -10× ]N=11.34N
1
2
3
2
N=Gcos300-Fsin300=[40 × - 10 × ]N=29.64N
1
2
3
2
一物体放在水平桌面上,现对物体施加一个斜向上的拉力F,使物体在水平桌面上做匀速直线运动.下面说法正确的是:
A.物体不一定受摩擦力作用
B.物体所受的滑动摩擦力与F的合外力一定为0
C.物体所受的滑动摩擦力与F的合外力一定向前
D.物体所受的滑动摩擦力与F的合外力一定向上
物体运动方向
如图,重为G的光滑小球用细绳悬挂在墙壁上的O点,细绳与竖直方面的夹角为?.小球对细绳的拉力及对墙壁的压力有多大?如果加大细绳的长度,使悬挂点由O点上移到O’,小球对墙壁的压力和对细绳的拉力如何变化?
O
O’
O
O’
G
N
F
x
y
当将绳子加长,悬挂点上移到O’时, ?减小
因此,绳子拉力F减小,N减小
小球对绳子的拉力大小等于F,对墙壁的压力大小等于N.因此,变化情况同F和N一样.
N - Fsin? =0 Fcos? - G=0
F =G/ cos? N = Fsin? = Gtan?
如图,重为G的物块放置在倾角为?的斜面上,在水平外力F的作用下保持静止状态.若将水平外力增大一些(物块仍静止),则有:
A.物块所受摩擦力一定增大
B.物块所受摩擦力一定减小
C.物块所受最大静摩擦力一定增大
D.以上都不对
F
F
N
G
x
y
当Gsin?> Fcos?时,静摩擦力f方向应该沿斜面向上,大小为(Gsin? - Fcos?).
当Gsin?< Fcos?时,静摩擦力f方向应该沿斜面向下,大小为(Fcos? - Gsin?).
因此,当F增大时,f可能增大也可能减小.
在y轴有:
N - Gcos? - Fsin?=0
因此,N= Gcos? + Fsin?
当F增大时,压力N增大.因此,最大静摩擦力增大.
总结
力学相关计算题解题一般步骤:
1.对物体进行受力分析.
2.建立直角坐标系,将力沿两个坐标轴分解.根据“同向相加,异向相减”的原则分别得出两坐标轴方向上的合力.
3.根据物体的状态得出各坐标轴上合力的值.如果物体处于平衡状态,则两个坐标轴上的合力都为0.
4.根据列出的关系式求解未知量.
在上面的例题中,如果斜面重100N,求地面对斜面的支持力(假设地面与斜面间无摩擦).
以水平方向和竖直方向为x轴和y轴,将木块对斜面的压力及木块与斜面之间的摩擦力分解在这两个方向上.
X轴:fcos? - N’sin? =0
y轴: N - fsin? - N’cos? - G= 0
N = fsin? + N’cos? + G
f
N’
G
N
x
y
?
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
