乘法运算律 课件人教新课标 (共36张PPT)
文档属性
| 名称 | 乘法运算律 课件人教新课标 (共36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-26 00:00:00 | ||
图片预览










文档简介
课件36张PPT。【学习目标】1.引导学生探索和理解乘法交换律、结合律和分配律,能运用运算定律进行一些简便计算。
2.培养学生根据具体情况,选择算法的意识与能力,发展思维的灵活性。
3.使学生感受数学与现实生活的联系,能用所学知识解决简单的实际问题。一、复习引入问题:1. 我们已经学过了哪些运算定律?2. 我们是怎样研究加法运算定律的?(加法交换律和加法结合律。) 教师引领学生回忆学习加法运算定律的学习过程:
? 初步发现规律;
? 枚举中验证规律;
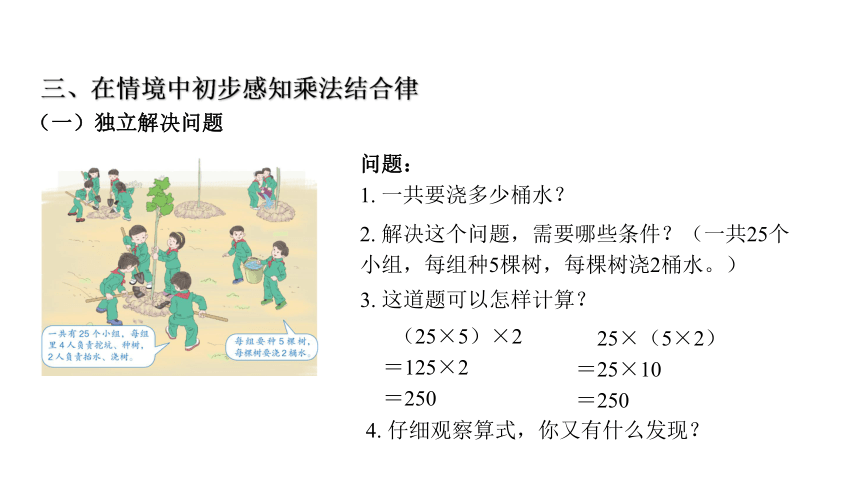
? 比较中概括规律。(一)收集信息,明确条件问题 问题:从图中你都知道了哪些信息?你是怎样理解这些信息的?预设① :每组4人负责挖坑、种树,2人负责抬水、浇树。(每组一共6人。)预设② :每组要种5棵树,每棵树要浇2桶水。(6人对应5棵树,每棵树要浇2桶水。)预设③ :一共有25个小组。二、在情境中初步感知乘法交换律问题:
1. 负责挖坑、种树的一共有多少人?2. 根据题意,你能列式解答吗?
(学生独立思考,解答问题两种不同的列式均板书)4×25=100 或 25×4=100(二)提出问题,独立尝试解决二、在情境中初步感知乘法交换律1. 你还能举出像这样的等式吗?(展示学生的举例,4~5组。)问题:我们已经学习过一些运算定律,借助以往的学习经验,你能继续研究吗?你有什么发现?(学生先独立思考,然后小组内交流自己的想法和发现。)3. 你能用自己喜欢的方式表示乘法交换律吗?
(展示大家的表示方法,让学生自己进行比较。)2. 观察这些算式,有什么特点?
(两个数相乘,交换两个因数的位置,积不变。这叫做乘法交换律)(三)枚举中验证规律,比较中概括规律二、在情境中初步感知乘法交换律问题: 1. 一共要浇多少桶水?3. 这道题可以怎样计算?2. 解决这个问题,需要哪些条件?(一共25个小组,每组种5棵树,每棵树浇2桶水。)4. 仔细观察算式,你又有什么发现? (25×5)×2
=125×2
=250 25×(5×2)
=25×10
=250(一)独立解决问题三、在情境中初步感知乘法结合律1. 你还能举出像这样的等式吗?(展示学生的举例, 4~5组。)问题:谁能把你的发现和大家交流一下?3. 你能用自己喜欢的方式表示乘法结合律吗?
(展示大家的表示方法,让学生自己进行比较。)2. 观察这些算式,有什么特点?
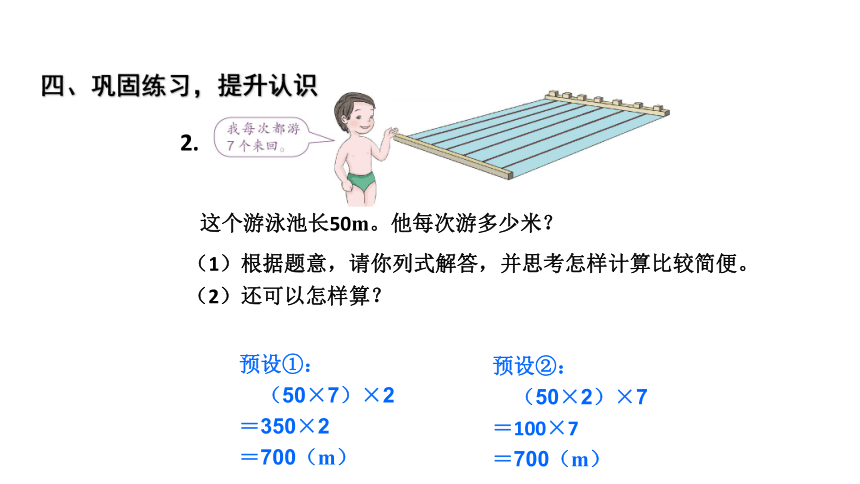
(三个数相乘,先乘前两个数,或者先乘后两个数,积不变这叫做乘法结合律)(二)迁移学习经验概括规律三、在情境中初步感知乘法结合律1. 根据乘法运算定律,在 里填上适当的数。1525482514858四、巩固练习,提升认识(1)根据题意,请你列式解答,并思考怎样计算比较简便。预设①:
(50×7)×2
=350×2
=700(m)(2)还可以怎样算?预设②:
(50×2)×7
=100×7
=700(m)这个游泳池长50m。他每次游多少米?2. 四、巩固练习,提升认识作业:第28页练习七,第10题。四、布置作业乘法分配律1. 我们已经研究了乘法的哪些运算定律?2. 对于运算定律的研究,我们已经积累了哪些经验?(教师引领学生回忆学习过程:
? 初步发现规律;
? 枚举中验证规律;
? 比较中概括规律。)一、复习引入问题:
1. 从图中你都知道了哪些信息?一共有多少名同学参加了这次植树活动?2. 要想解决问题,需要用到哪些条件? “一共有25个小组,每组里4人负责挖坑、种树,2人负责抬水、浇树。”(一)收集信息,明确条件问题三、在情境中初步感知乘法分配律1. 根据题意,你能列式解答吗?有没有不同的方法?2. 谁能说一说这样做的道理? (4+2)×25
=6×25
=150 4×25+2×25
=100+50
=1503. 有没有不同的做法?(先算出每一组植树的有6人,再乘25个组,就是一共植树的人数。)(分别算出25个小组挖坑、种树的人数和25个小组抬水、浇树的人数,把这两部分加在一起,就是一共植树的人数。)(二)独立解决,思考不同方法二、在情境中初步感知乘法分配律2. 你还能举出像这样的等式吗?(展示学生的举例,4~5组。)这两种做法有什么相同点和不同点?
(相同点:结果相等,(4+2)×25=4×25+2×25。)4. 你能用自己喜欢的方式表示乘法分配律吗? 3. 观察这些算式,有什么特点?(两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加这叫做乘法分配律)(三)枚举验证,比较概括规律二、在情境中初步感知乘法分配律1. 下面哪些算式是正确的?正确的画“√”,错误的 画“×”。56×(19+28)=56×19+28 ( )32×(7×3)=32×7+32×3 ( )64×64+36×64=(64+36)×64 ( )××√说一说你的判断理由。三、巩固练习,提升认识117×3+117×7=117×(3+7)24×(5+12)=24×174×a+a×5=(4+5)×a36×(4×6)=36×6×42. 下面哪些算式运用了乘法分配律?三、巩固练习,提升认识根据题意,你能列式计算吗?说一说你这样计算的理由。 (75+45)×60
=120×60
=7200(元)监控:75和45可以凑整,计算比较简便。3. 李阿姨购进了60套这种运动服,花了多少钱?三、巩固练习,提升认识运用了乘法分配律:
25×12=25×2+25×104. 观察下面的竖式,说一说在计算的过程中运用了什么运算定律。三、巩固练习,提升认识103×12问题:观察数据的特点,说一说怎样计算比较简便。=(100+3)×12
=100×12+3×12
=1200+36
=123620×55=20×(50+5)
=20×50+20×5
=1000+100
=11005. 用乘法分配律计算下面各题。三、巩固练习,提升认识作业:第28页练习七,第7题。四、布置作业解决问题(例8)说一说我们已经学过哪些运算定律,并用字母表示。加法交换律:a+b=b+a 加法结合律:(a+b)+c=a+(b+c)乘法交换律:a×b=b×a乘法结合律:(a×b)×c=a×(b×c)乘法分配律:a×(b+c)=a×b+a×c在解决问题时,灵活地运用这些运算定律,可以使计算变得简便。一、复习导入(5副羽毛球拍,共330元。25筒羽毛球,每筒32元。注意引导学生观察羽毛球的包装上的信息,“一打”是12个。)王老师一共买了多少个羽毛球?(一)收集信息,明确条件问题二、创设情境,灵活运用问题:解决这个问题,需要哪些信息?你能根据所选的信息,解决这个问题吗?(买了25筒羽毛球、“一打”装、“一打”是12个。)王老师一共买了多少个羽毛球?(二)独立思考,尝试解决问题二、创设情境,灵活运用问题:1. 你还有别的计算方法吗? 2. 谁能说一说你对这种解法的理解?预设②:3. 比较3种不同的解法,你喜欢哪种?说一说你的理由。(后两种方法都关注到了数字的特点,利用运算定律使计算变得简便。) 12×25
=(3×4)×25
=3×(4×25)
=3×100
=300 12×25
=(10+2)×25
=10×25+2×25
=250+50
=300预设①:预设③:(三)读懂过程,感悟不同方法二、创设情境,灵活运用2. 这些不同的算法中有什么相同点与不同点?问题:1. 怎样检验结果是否正确?3. 在解决实际问题时,我们要注意什么?
(关注数据的特点,灵活运用运算定律,使计算变得简便。)预设②: 12×25
=(3×4)×25
=3×(4×25)
=3×100
=300 12×25
=(10+2)×25
=10×25+2×25
=250+50
=300预设①:预设③:(四)回顾反思,沟通不同方法二、创设情境,灵活运用每支羽毛球拍多少钱?问题:解决这个问题,需要哪些信息?你能根据所选的信息,解决这个问题吗?(学生独立解决问题。)(一)独立尝试,解决问题三、自主探索,发现新知预设①:问题:1. 330÷5后,为什么还要÷2?2. 还有不同的计算方法吗?(要求每支羽毛球拍多少钱,330÷5求的是一副羽毛球拍的价格。) 330÷5÷2
=66÷2
=33(二)比较观察,发现规律三、自主探索,发现新知 330÷5÷2
=66÷2
=33预设②:问题:1. 你能理解这位同学的想法吗?2. 为什么330÷5÷2和330÷(5×2)之间可以用等号连接?3. 观察算式的特点,看看你能发现什么规律。 330÷5÷2
=330÷(5×2)
=330÷10
=33(先求一共有10支羽毛球拍,再求每支羽毛球拍的价格。)(①它们的结果相等。②都是求一支羽毛球拍的价格。)(一个数连续除以两个数,可以除以后两个数的乘积。)预设①:(二)比较观察,发现规律三、自主探索,发现新知1. 350÷14
=350÷(7×2)
=350÷7÷2
=50÷2
=25(册)
答:平均每个班可以分到25册。(2)观察数据,有什么特点?问题:
(1)你知道了什么?(3)怎样计算比较简便?四、巩固练习,提升认识问题:(1)你知道了什么?(3)谁读懂了他的意思?说一说。(4)谁的想法和他的不一样?能再说说吗?(2)你能解决这个问题吗?写出你的思考过程。(5)你做的正确吗?这学期一共有多少天?2. 四、巩固练习,提升认识 9×21+9×19
=9×(21+19)
=9×40
=360(m2 )答:这块菜地的面积有360 m2。3. 李大爷家有一块菜地(如右图),这块菜地的面积有多少平方米?四、巩固练习,提升认识作业:第30页练习八,第3题;
第31页练习八,第7题。五、布置任务
2.培养学生根据具体情况,选择算法的意识与能力,发展思维的灵活性。
3.使学生感受数学与现实生活的联系,能用所学知识解决简单的实际问题。一、复习引入问题:1. 我们已经学过了哪些运算定律?2. 我们是怎样研究加法运算定律的?(加法交换律和加法结合律。) 教师引领学生回忆学习加法运算定律的学习过程:
? 初步发现规律;
? 枚举中验证规律;
? 比较中概括规律。(一)收集信息,明确条件问题 问题:从图中你都知道了哪些信息?你是怎样理解这些信息的?预设① :每组4人负责挖坑、种树,2人负责抬水、浇树。(每组一共6人。)预设② :每组要种5棵树,每棵树要浇2桶水。(6人对应5棵树,每棵树要浇2桶水。)预设③ :一共有25个小组。二、在情境中初步感知乘法交换律问题:
1. 负责挖坑、种树的一共有多少人?2. 根据题意,你能列式解答吗?
(学生独立思考,解答问题两种不同的列式均板书)4×25=100 或 25×4=100(二)提出问题,独立尝试解决二、在情境中初步感知乘法交换律1. 你还能举出像这样的等式吗?(展示学生的举例,4~5组。)问题:我们已经学习过一些运算定律,借助以往的学习经验,你能继续研究吗?你有什么发现?(学生先独立思考,然后小组内交流自己的想法和发现。)3. 你能用自己喜欢的方式表示乘法交换律吗?
(展示大家的表示方法,让学生自己进行比较。)2. 观察这些算式,有什么特点?
(两个数相乘,交换两个因数的位置,积不变。这叫做乘法交换律)(三)枚举中验证规律,比较中概括规律二、在情境中初步感知乘法交换律问题: 1. 一共要浇多少桶水?3. 这道题可以怎样计算?2. 解决这个问题,需要哪些条件?(一共25个小组,每组种5棵树,每棵树浇2桶水。)4. 仔细观察算式,你又有什么发现? (25×5)×2
=125×2
=250 25×(5×2)
=25×10
=250(一)独立解决问题三、在情境中初步感知乘法结合律1. 你还能举出像这样的等式吗?(展示学生的举例, 4~5组。)问题:谁能把你的发现和大家交流一下?3. 你能用自己喜欢的方式表示乘法结合律吗?
(展示大家的表示方法,让学生自己进行比较。)2. 观察这些算式,有什么特点?
(三个数相乘,先乘前两个数,或者先乘后两个数,积不变这叫做乘法结合律)(二)迁移学习经验概括规律三、在情境中初步感知乘法结合律1. 根据乘法运算定律,在 里填上适当的数。1525482514858四、巩固练习,提升认识(1)根据题意,请你列式解答,并思考怎样计算比较简便。预设①:
(50×7)×2
=350×2
=700(m)(2)还可以怎样算?预设②:
(50×2)×7
=100×7
=700(m)这个游泳池长50m。他每次游多少米?2. 四、巩固练习,提升认识作业:第28页练习七,第10题。四、布置作业乘法分配律1. 我们已经研究了乘法的哪些运算定律?2. 对于运算定律的研究,我们已经积累了哪些经验?(教师引领学生回忆学习过程:
? 初步发现规律;
? 枚举中验证规律;
? 比较中概括规律。)一、复习引入问题:
1. 从图中你都知道了哪些信息?一共有多少名同学参加了这次植树活动?2. 要想解决问题,需要用到哪些条件? “一共有25个小组,每组里4人负责挖坑、种树,2人负责抬水、浇树。”(一)收集信息,明确条件问题三、在情境中初步感知乘法分配律1. 根据题意,你能列式解答吗?有没有不同的方法?2. 谁能说一说这样做的道理? (4+2)×25
=6×25
=150 4×25+2×25
=100+50
=1503. 有没有不同的做法?(先算出每一组植树的有6人,再乘25个组,就是一共植树的人数。)(分别算出25个小组挖坑、种树的人数和25个小组抬水、浇树的人数,把这两部分加在一起,就是一共植树的人数。)(二)独立解决,思考不同方法二、在情境中初步感知乘法分配律2. 你还能举出像这样的等式吗?(展示学生的举例,4~5组。)这两种做法有什么相同点和不同点?
(相同点:结果相等,(4+2)×25=4×25+2×25。)4. 你能用自己喜欢的方式表示乘法分配律吗? 3. 观察这些算式,有什么特点?(两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加这叫做乘法分配律)(三)枚举验证,比较概括规律二、在情境中初步感知乘法分配律1. 下面哪些算式是正确的?正确的画“√”,错误的 画“×”。56×(19+28)=56×19+28 ( )32×(7×3)=32×7+32×3 ( )64×64+36×64=(64+36)×64 ( )××√说一说你的判断理由。三、巩固练习,提升认识117×3+117×7=117×(3+7)24×(5+12)=24×174×a+a×5=(4+5)×a36×(4×6)=36×6×42. 下面哪些算式运用了乘法分配律?三、巩固练习,提升认识根据题意,你能列式计算吗?说一说你这样计算的理由。 (75+45)×60
=120×60
=7200(元)监控:75和45可以凑整,计算比较简便。3. 李阿姨购进了60套这种运动服,花了多少钱?三、巩固练习,提升认识运用了乘法分配律:
25×12=25×2+25×104. 观察下面的竖式,说一说在计算的过程中运用了什么运算定律。三、巩固练习,提升认识103×12问题:观察数据的特点,说一说怎样计算比较简便。=(100+3)×12
=100×12+3×12
=1200+36
=123620×55=20×(50+5)
=20×50+20×5
=1000+100
=11005. 用乘法分配律计算下面各题。三、巩固练习,提升认识作业:第28页练习七,第7题。四、布置作业解决问题(例8)说一说我们已经学过哪些运算定律,并用字母表示。加法交换律:a+b=b+a 加法结合律:(a+b)+c=a+(b+c)乘法交换律:a×b=b×a乘法结合律:(a×b)×c=a×(b×c)乘法分配律:a×(b+c)=a×b+a×c在解决问题时,灵活地运用这些运算定律,可以使计算变得简便。一、复习导入(5副羽毛球拍,共330元。25筒羽毛球,每筒32元。注意引导学生观察羽毛球的包装上的信息,“一打”是12个。)王老师一共买了多少个羽毛球?(一)收集信息,明确条件问题二、创设情境,灵活运用问题:解决这个问题,需要哪些信息?你能根据所选的信息,解决这个问题吗?(买了25筒羽毛球、“一打”装、“一打”是12个。)王老师一共买了多少个羽毛球?(二)独立思考,尝试解决问题二、创设情境,灵活运用问题:1. 你还有别的计算方法吗? 2. 谁能说一说你对这种解法的理解?预设②:3. 比较3种不同的解法,你喜欢哪种?说一说你的理由。(后两种方法都关注到了数字的特点,利用运算定律使计算变得简便。) 12×25
=(3×4)×25
=3×(4×25)
=3×100
=300 12×25
=(10+2)×25
=10×25+2×25
=250+50
=300预设①:预设③:(三)读懂过程,感悟不同方法二、创设情境,灵活运用2. 这些不同的算法中有什么相同点与不同点?问题:1. 怎样检验结果是否正确?3. 在解决实际问题时,我们要注意什么?
(关注数据的特点,灵活运用运算定律,使计算变得简便。)预设②: 12×25
=(3×4)×25
=3×(4×25)
=3×100
=300 12×25
=(10+2)×25
=10×25+2×25
=250+50
=300预设①:预设③:(四)回顾反思,沟通不同方法二、创设情境,灵活运用每支羽毛球拍多少钱?问题:解决这个问题,需要哪些信息?你能根据所选的信息,解决这个问题吗?(学生独立解决问题。)(一)独立尝试,解决问题三、自主探索,发现新知预设①:问题:1. 330÷5后,为什么还要÷2?2. 还有不同的计算方法吗?(要求每支羽毛球拍多少钱,330÷5求的是一副羽毛球拍的价格。) 330÷5÷2
=66÷2
=33(二)比较观察,发现规律三、自主探索,发现新知 330÷5÷2
=66÷2
=33预设②:问题:1. 你能理解这位同学的想法吗?2. 为什么330÷5÷2和330÷(5×2)之间可以用等号连接?3. 观察算式的特点,看看你能发现什么规律。 330÷5÷2
=330÷(5×2)
=330÷10
=33(先求一共有10支羽毛球拍,再求每支羽毛球拍的价格。)(①它们的结果相等。②都是求一支羽毛球拍的价格。)(一个数连续除以两个数,可以除以后两个数的乘积。)预设①:(二)比较观察,发现规律三、自主探索,发现新知1. 350÷14
=350÷(7×2)
=350÷7÷2
=50÷2
=25(册)
答:平均每个班可以分到25册。(2)观察数据,有什么特点?问题:
(1)你知道了什么?(3)怎样计算比较简便?四、巩固练习,提升认识问题:(1)你知道了什么?(3)谁读懂了他的意思?说一说。(4)谁的想法和他的不一样?能再说说吗?(2)你能解决这个问题吗?写出你的思考过程。(5)你做的正确吗?这学期一共有多少天?2. 四、巩固练习,提升认识 9×21+9×19
=9×(21+19)
=9×40
=360(m2 )答:这块菜地的面积有360 m2。3. 李大爷家有一块菜地(如右图),这块菜地的面积有多少平方米?四、巩固练习,提升认识作业:第30页练习八,第3题;
第31页练习八,第7题。五、布置任务
