五年级下册数学一课一练4.3长方体的体积北师大版(含答案)
文档属性
| 名称 | 五年级下册数学一课一练4.3长方体的体积北师大版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 72.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-27 10:08:18 | ||
图片预览



文档简介
五年级下册数学一课一练-4.3长方体的体积
一、单选题
1.如下图所示,用相同的小正方体搭成的两个长方体,它们的体积( ? ?? )。
A.一样大 B.第一个大 C.第二个大
2.表面积是96 的正方体,它的体积是(?? )
A.16 B.32 C.64
3.一个长方体的底面积是0.8m2 , 倒入水后,水面高为5cm,倒入了( ??)L水。
A.4 B.40 C.400
4.体积是(?? )
A.0.32 B.0.1 C.0.8 D.0.16
5.底面积和高均相等的正方体、长方体、圆柱相比较,它们的体积,(?? )。
A.正方体体积大 B.长方体体积大 C.圆柱体体积大 D.一样大
二、判断题
6.长方体、正方体、圆柱和圆锥的体积都可以用“底面积×高”计算。
7.棱长6厘米的正方体表面积与体积相等。
8.表面积相等的两个长方体,它们的体积一定相等。
9.棱长1分米的正方体的表面积比它的体积大。
10.一个底面积是5平方米,高1.5米的长方体的体积是7.5立方米。
三、填空题
11.爸爸收到一件礼物,这个长方体的礼物盒的长和宽都是25cm,高是8cm,它的体积是________cm3。
12.一个长方体长8厘米,宽5厘米,高2厘米.它的表面积是________平方厘米,体积是________立方厘米.
13.填表
________
14.一个正方体的棱长之和是48分米,它的表面积是________分米2 , 体积是________分米3 .
15.两个立方体的棱长之比是2∶3,那么它们的表面积比是________,体积比是________。
16.一个正方体,容积是216升,把这一箱油的 倒入一个长4分米,宽2.5分米的长方体油箱内,这个油箱内的油高________分米。
17.用一根长48厘米的铁丝焊接成一个正方体框架(接头处不计),其表面积是________? ,体积是________ .
四、解答题
18.一个长方体玻璃缸,底面长8dm、宽6dm。如果要向这个池子里注入3dm高的水,需要多少升水?
19.一个长方体木料的体积是600dm3 , 它的横截面的面积是12dm2 , 它的高是多少米?
五、综合题
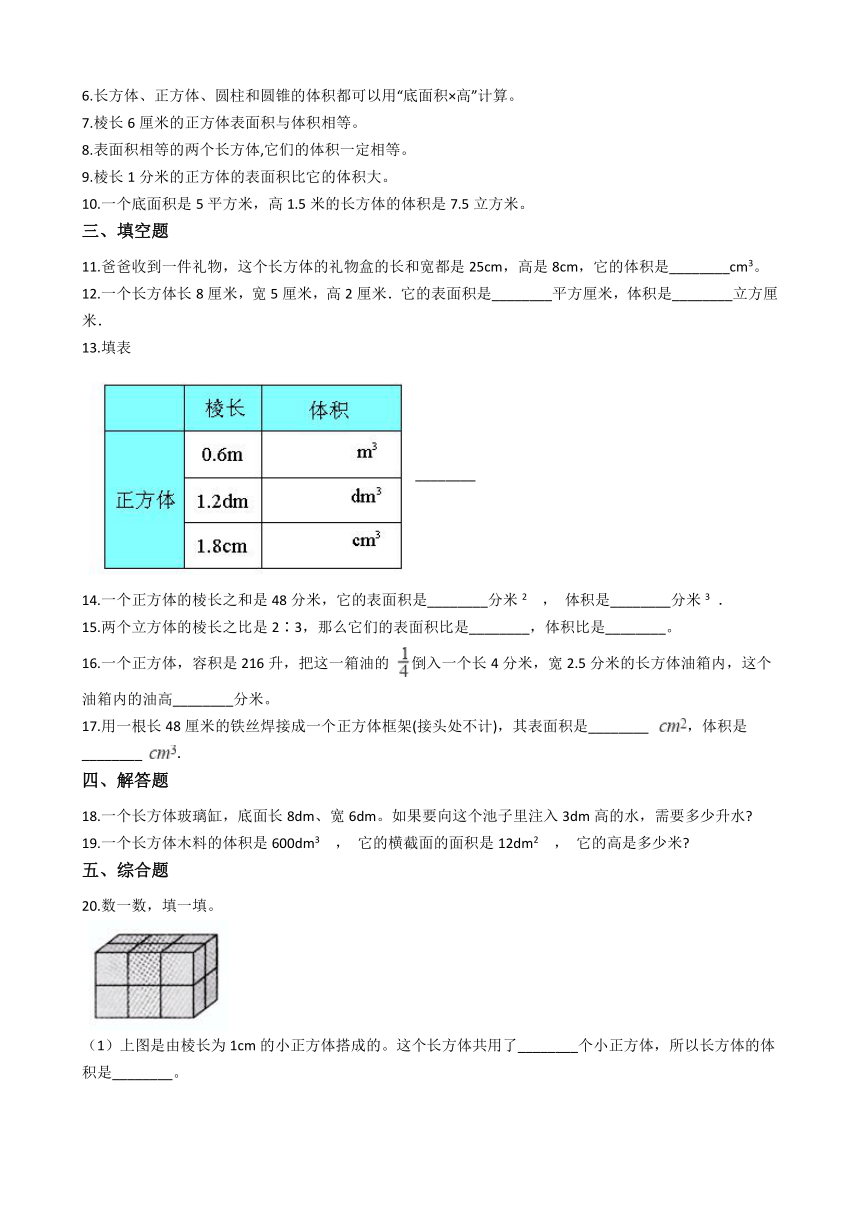
20.数一数,填一填。
(1)上图是由棱长为1cm的小正方体搭成的。这个长方体共用了________个小正方体,所以长方体的体积是________。
(2)通过观察发现:小正方体的总个数可以用长方体的________×________×________迅速求出,所以推得长方体的体积=________×________×________,用字母表示是________。
六、应用题
21.一个长方形水箱,长5分米,宽4分米,高3分米.装满水后倒入一个棱长是5分米的水箱内,水深多少分米?
22.个长方体水箱,从里面量长8分米,宽6分米,深5分米.里面装着水,水面距上口1.5分米.
①这个水箱的容积是多少升?
②水箱内水的体积是多少?
③如果用铁皮做这样一个水箱,至少需要铁皮多少平方分米?
答案解析部分
一、单选题
1.【答案】 C
【解析】【解答】数一数可知,图形1的体积是4,图形2的体积是6,4<6,第二个图形的体积大些. 故答案为:C 【分析】观察图可知,用相同的小正方体搭不同的长方体,数一数有几个小正方体,体积就是几,据此比较大小.
2.【答案】 C
【解析】【解答】正方体的一个面面积:96÷6=16(cm); 因为16=4×4,所以正方体的棱长是4cm, 正方体的体积: 4×4×4 =16×4 =64(cm3) 故答案为:C. 【分析】根据正方体的表面积=一个面的面积×6,已知正方体的表面积,求一个面的面积,用正方体的表面积÷6=一个面的面积,然后根据一个面的面积,求出正方体的棱长,最后根据正方体的体积=棱长×棱长×棱长,据此列式解答.
3.【答案】 B
【解析】【解答】0.8m2=0.8×100=80(dm2), 5cm=5÷10=0.5(dm), 80×0.5=40(dm3)=40(L). 故答案为:B. 【分析】根据题意可知,先把单位化统一,m2化成dm2 , 乘进率100,cm化成dm,除以进率10,然后用长方体的底面积×高=水的体积,根据1dm3=1L,将体积单位化成L,据此解答.
4.【答案】D
【解析】【解答】解:1.6×0.5×0.2=0.16(m3) 故答案为:D。
【分析】长方体体积=长×宽×高,由此根据公式计算即可。
5.【答案】 D
【解析】【解答】 底面积和高均相等的正方体、长方体、圆柱相比较,它们的体积一样大。 故答案为:D。
【分析】 对于底面积和高均相等的正方体、长方体、圆柱,它们的体积公式都可用 V=Sh 来表示,据此可得出答案。
二、判断题
6.【答案】 错误
【解析】【解答】解:长方体、正方体、圆柱可以用“底面积×高”计算,圆锥的体积=底面积×高×。原题说法错误。 故答案为:错误。
【分析】长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,长×宽是长方体的底面积,棱长×棱长是正方体的底面积;圆柱的体积=底面积×高,圆锥的体积=底面积×高×。
7.【答案】错误
【解析】【解答】解:棱长6厘米的正方体表面积和体积不相等,原题说法错误。 故答案为:错误。
【分析】表面积和体积的意义不同,无法比较大小,因此正方体表面积与体积是不可能相等的。
8.【答案】 错误
【解析】【解答】根据分析可得,例如:长宽高分别为4,8,12的长方体表面积为: (4×8+4×12+8×12)×2 =(32+48+96)×2 =176×2 =352, 体积为: 4×8×12 =32×12 =384; 长宽高分别为4,4,20的长方体表面积为: (4×4+4×20+4×20)×2 =(16+80+80)×2 =176×2 =352, 体积为: 4×4×20 =16×20 =320; 表面积相等的两个长方体,它们的体积不一定相等,原题说法错误. 故答案为:错误.
【分析】此题主要考查了长方体的表面积和体积的计算,可以用举例的方法,列举两个表面积相等的长方体,通过计算发现体积不相等,据此解答.
9.【答案】 错误
【解析】【解答】正方体的表面积和体积无法比较大小,原题说法错误. 故答案为:错误. 【分析】所有立体图形外面的面积之和叫做它的表面积,体积指物体所占空间的大小,表面积和体积无法比较大小,据此判断.
10.【答案】 正确
【解析】【解答】解:5×1.5=7.5(立方米),故“一个底面积是5平方米,高1.5米的长方体的体积是7.5立方米”这个说法是正确的。 ?故答案为:正确。 【分析】长方体体积=长×宽×高=底面积×高。
三、填空题
11.【答案】5000
【解析】【解答】25×25×8 =625×8 =5000(cm3) 故答案为:5000.【分析】已知长方体的长、宽、高,求长方体的体积,用公式:长方体的体积=长×宽×高,据此列式解答.
12.【答案】 132;80
【解析】【解答】长方体的表面积: (8×5+8×2+5×2)×2 =(40+16+10)×2 =66×2 =132(平方厘米) 长方体的体积: 8×5×2 =40×2 =80(立方厘米) 故答案为:132;80.
【分析】已知长方体的长、宽、高,求长方体的表面积,用公式:长方体的表面积=(长×宽+长×高+宽×高)×2,求长方体的体积,用公式:长方体的体积=长×宽×高,据此列式解答.
13.【答案】0.216,1.728,5.832
【解析】【解答】解:0.6×0.6×0.6=0.216(m3);1.2×1.2×1.2=1.728(dm3);1.8×1.8×1.8=5.832(cm3)。 故答案为:0.216;1.728;5.832。
【分析】正方体体积=棱长×棱长×棱长,由此根据公式分别计算即可。
14.【答案】 96;64
【解析】【解答】解:棱长:48÷12=4(分米),表面积:4×4×6=96(平方分米),体积:4×4×4=64(立方分米) 故答案为:96;64
【分析】用正方体棱长和除以12求出棱长,然后计算表面积和体积,正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长。
15.【答案】4:9;8:27
【解析】【解答】解:表面积的比是4:9,体积比是8:27。 故答案为:4:9;8:27
【分析】根据正方体表面积和体积公式可知,正方体的表面积的比是棱长的平方的比,体积比是棱长的立方的比。
16.【答案】 5.4
【解析】【解答】解:216×÷(4×2.5) =54÷10 =5.4(分米) 故答案为:5.4
【分析】用正方体的容积乘求出倒入油箱油的容积,然后除以长方体油箱的底面积即可求出油的高度。
17.【答案】 96;64
【解析】【解答】解:48÷12=4(厘米),表面积:4×4×6=96(立方厘米),体积:4×4×4=64(立方厘米) 故答案为:96;64 ???????????
【分析】铁丝的长度就是正方体的棱长和,用棱长和除以12求出棱长;正方体体积=棱长×棱长×棱长,正方体表面积=棱长×棱长×6,根据公式计算。
四、解答题
18.【答案】 解:8×6×3=144(dm3)=144(L)
答:需要144升水。
【解析】【分析】根据题意可知,用公式:长方体的体积=长×宽×高,据此列式计算,然后根据1立方分米=1升,将立方分米化成升即可.
19.【答案】 解:600÷12=50(dm)
50dm=5m
答:它的高是5米。
【解析】【分析】长方体体积=底面积×高,用长方体木料的体积除以横截面的面积即可求出木料的高。
五、综合题
20.【答案】 (1)12;12cm3 (2)长;宽;高;长;宽;高;V=abh
【解析】【解答】 ?
(1)上图是由棱长为1cm的小正方体搭成的。这个长方体共用了12个小正方体,所以长方体的体积是12cm3. (2) 通过观察发现:小正方体的总个数可以用长方体的长×宽×高迅速求出,所以推得长方体的体积=长×宽×高,用字母表示是:V=abh.
故答案为:(1)12;12cm3;(2)长;宽;高;长;宽;高;V=abh. 【分析】(1)观察图可知,图中的长方体是由棱长为1cm的小正方体搭成的,每个小正方体的体积是1cm3 , 数一数用了几个小正方体,这个长方体的体积就是几立方厘米; (2)观察可以发现:小正方体的总个数可以用长方体的长×宽×高迅速求出,所以推得长方体的体积=长×宽×高,用字母表示是:V=abh,据此解答.
六、应用题
21.【答案】 解:设水深为x分米.
5×5×x=5×4×3 ?? ???????? x=60÷25 ???????? x=2.4
或:5×4×3÷(5×5)=2.4(分米) 答:水深24分米。
【解析】【分析】长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,设水深x分米,根据水的体积相等列出方程,解方程求出水深;用水的体积除以水箱的底面积也可以求出水深。
22.【答案】解:①8×6×5=240(立方分米),240立方分米=240升
②8×6×(5-1.5)=48×3.5=168(立方分米)
或240-8×6×1.5=240-72=168(立方分米)
③(8×6+6×5+5×8)×2 =(48+30+40)×2 =118×2 =236(平方分米) 答:①这个水箱的容积是240升;②水箱内水的体积是168立方分米;③至少需要236平方分米的铁皮。
【解析】【分析】①用水箱的长乘宽乘高求出容积;②用长方体的底面积乘水面的高度求出水的体积;③长方体表面积=(长×宽+长×高+宽×高)×2,根据表面积公式计算。
一、单选题
1.如下图所示,用相同的小正方体搭成的两个长方体,它们的体积( ? ?? )。
A.一样大 B.第一个大 C.第二个大
2.表面积是96 的正方体,它的体积是(?? )
A.16 B.32 C.64
3.一个长方体的底面积是0.8m2 , 倒入水后,水面高为5cm,倒入了( ??)L水。
A.4 B.40 C.400
4.体积是(?? )
A.0.32 B.0.1 C.0.8 D.0.16
5.底面积和高均相等的正方体、长方体、圆柱相比较,它们的体积,(?? )。
A.正方体体积大 B.长方体体积大 C.圆柱体体积大 D.一样大
二、判断题
6.长方体、正方体、圆柱和圆锥的体积都可以用“底面积×高”计算。
7.棱长6厘米的正方体表面积与体积相等。
8.表面积相等的两个长方体,它们的体积一定相等。
9.棱长1分米的正方体的表面积比它的体积大。
10.一个底面积是5平方米,高1.5米的长方体的体积是7.5立方米。
三、填空题
11.爸爸收到一件礼物,这个长方体的礼物盒的长和宽都是25cm,高是8cm,它的体积是________cm3。
12.一个长方体长8厘米,宽5厘米,高2厘米.它的表面积是________平方厘米,体积是________立方厘米.
13.填表
________
14.一个正方体的棱长之和是48分米,它的表面积是________分米2 , 体积是________分米3 .
15.两个立方体的棱长之比是2∶3,那么它们的表面积比是________,体积比是________。
16.一个正方体,容积是216升,把这一箱油的 倒入一个长4分米,宽2.5分米的长方体油箱内,这个油箱内的油高________分米。
17.用一根长48厘米的铁丝焊接成一个正方体框架(接头处不计),其表面积是________? ,体积是________ .
四、解答题
18.一个长方体玻璃缸,底面长8dm、宽6dm。如果要向这个池子里注入3dm高的水,需要多少升水?
19.一个长方体木料的体积是600dm3 , 它的横截面的面积是12dm2 , 它的高是多少米?
五、综合题
20.数一数,填一填。
(1)上图是由棱长为1cm的小正方体搭成的。这个长方体共用了________个小正方体,所以长方体的体积是________。
(2)通过观察发现:小正方体的总个数可以用长方体的________×________×________迅速求出,所以推得长方体的体积=________×________×________,用字母表示是________。
六、应用题
21.一个长方形水箱,长5分米,宽4分米,高3分米.装满水后倒入一个棱长是5分米的水箱内,水深多少分米?
22.个长方体水箱,从里面量长8分米,宽6分米,深5分米.里面装着水,水面距上口1.5分米.
①这个水箱的容积是多少升?
②水箱内水的体积是多少?
③如果用铁皮做这样一个水箱,至少需要铁皮多少平方分米?
答案解析部分
一、单选题
1.【答案】 C
【解析】【解答】数一数可知,图形1的体积是4,图形2的体积是6,4<6,第二个图形的体积大些. 故答案为:C 【分析】观察图可知,用相同的小正方体搭不同的长方体,数一数有几个小正方体,体积就是几,据此比较大小.
2.【答案】 C
【解析】【解答】正方体的一个面面积:96÷6=16(cm); 因为16=4×4,所以正方体的棱长是4cm, 正方体的体积: 4×4×4 =16×4 =64(cm3) 故答案为:C. 【分析】根据正方体的表面积=一个面的面积×6,已知正方体的表面积,求一个面的面积,用正方体的表面积÷6=一个面的面积,然后根据一个面的面积,求出正方体的棱长,最后根据正方体的体积=棱长×棱长×棱长,据此列式解答.
3.【答案】 B
【解析】【解答】0.8m2=0.8×100=80(dm2), 5cm=5÷10=0.5(dm), 80×0.5=40(dm3)=40(L). 故答案为:B. 【分析】根据题意可知,先把单位化统一,m2化成dm2 , 乘进率100,cm化成dm,除以进率10,然后用长方体的底面积×高=水的体积,根据1dm3=1L,将体积单位化成L,据此解答.
4.【答案】D
【解析】【解答】解:1.6×0.5×0.2=0.16(m3) 故答案为:D。
【分析】长方体体积=长×宽×高,由此根据公式计算即可。
5.【答案】 D
【解析】【解答】 底面积和高均相等的正方体、长方体、圆柱相比较,它们的体积一样大。 故答案为:D。
【分析】 对于底面积和高均相等的正方体、长方体、圆柱,它们的体积公式都可用 V=Sh 来表示,据此可得出答案。
二、判断题
6.【答案】 错误
【解析】【解答】解:长方体、正方体、圆柱可以用“底面积×高”计算,圆锥的体积=底面积×高×。原题说法错误。 故答案为:错误。
【分析】长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,长×宽是长方体的底面积,棱长×棱长是正方体的底面积;圆柱的体积=底面积×高,圆锥的体积=底面积×高×。
7.【答案】错误
【解析】【解答】解:棱长6厘米的正方体表面积和体积不相等,原题说法错误。 故答案为:错误。
【分析】表面积和体积的意义不同,无法比较大小,因此正方体表面积与体积是不可能相等的。
8.【答案】 错误
【解析】【解答】根据分析可得,例如:长宽高分别为4,8,12的长方体表面积为: (4×8+4×12+8×12)×2 =(32+48+96)×2 =176×2 =352, 体积为: 4×8×12 =32×12 =384; 长宽高分别为4,4,20的长方体表面积为: (4×4+4×20+4×20)×2 =(16+80+80)×2 =176×2 =352, 体积为: 4×4×20 =16×20 =320; 表面积相等的两个长方体,它们的体积不一定相等,原题说法错误. 故答案为:错误.
【分析】此题主要考查了长方体的表面积和体积的计算,可以用举例的方法,列举两个表面积相等的长方体,通过计算发现体积不相等,据此解答.
9.【答案】 错误
【解析】【解答】正方体的表面积和体积无法比较大小,原题说法错误. 故答案为:错误. 【分析】所有立体图形外面的面积之和叫做它的表面积,体积指物体所占空间的大小,表面积和体积无法比较大小,据此判断.
10.【答案】 正确
【解析】【解答】解:5×1.5=7.5(立方米),故“一个底面积是5平方米,高1.5米的长方体的体积是7.5立方米”这个说法是正确的。 ?故答案为:正确。 【分析】长方体体积=长×宽×高=底面积×高。
三、填空题
11.【答案】5000
【解析】【解答】25×25×8 =625×8 =5000(cm3) 故答案为:5000.【分析】已知长方体的长、宽、高,求长方体的体积,用公式:长方体的体积=长×宽×高,据此列式解答.
12.【答案】 132;80
【解析】【解答】长方体的表面积: (8×5+8×2+5×2)×2 =(40+16+10)×2 =66×2 =132(平方厘米) 长方体的体积: 8×5×2 =40×2 =80(立方厘米) 故答案为:132;80.
【分析】已知长方体的长、宽、高,求长方体的表面积,用公式:长方体的表面积=(长×宽+长×高+宽×高)×2,求长方体的体积,用公式:长方体的体积=长×宽×高,据此列式解答.
13.【答案】0.216,1.728,5.832
【解析】【解答】解:0.6×0.6×0.6=0.216(m3);1.2×1.2×1.2=1.728(dm3);1.8×1.8×1.8=5.832(cm3)。 故答案为:0.216;1.728;5.832。
【分析】正方体体积=棱长×棱长×棱长,由此根据公式分别计算即可。
14.【答案】 96;64
【解析】【解答】解:棱长:48÷12=4(分米),表面积:4×4×6=96(平方分米),体积:4×4×4=64(立方分米) 故答案为:96;64
【分析】用正方体棱长和除以12求出棱长,然后计算表面积和体积,正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长。
15.【答案】4:9;8:27
【解析】【解答】解:表面积的比是4:9,体积比是8:27。 故答案为:4:9;8:27
【分析】根据正方体表面积和体积公式可知,正方体的表面积的比是棱长的平方的比,体积比是棱长的立方的比。
16.【答案】 5.4
【解析】【解答】解:216×÷(4×2.5) =54÷10 =5.4(分米) 故答案为:5.4
【分析】用正方体的容积乘求出倒入油箱油的容积,然后除以长方体油箱的底面积即可求出油的高度。
17.【答案】 96;64
【解析】【解答】解:48÷12=4(厘米),表面积:4×4×6=96(立方厘米),体积:4×4×4=64(立方厘米) 故答案为:96;64 ???????????
【分析】铁丝的长度就是正方体的棱长和,用棱长和除以12求出棱长;正方体体积=棱长×棱长×棱长,正方体表面积=棱长×棱长×6,根据公式计算。
四、解答题
18.【答案】 解:8×6×3=144(dm3)=144(L)
答:需要144升水。
【解析】【分析】根据题意可知,用公式:长方体的体积=长×宽×高,据此列式计算,然后根据1立方分米=1升,将立方分米化成升即可.
19.【答案】 解:600÷12=50(dm)
50dm=5m
答:它的高是5米。
【解析】【分析】长方体体积=底面积×高,用长方体木料的体积除以横截面的面积即可求出木料的高。
五、综合题
20.【答案】 (1)12;12cm3 (2)长;宽;高;长;宽;高;V=abh
【解析】【解答】 ?
(1)上图是由棱长为1cm的小正方体搭成的。这个长方体共用了12个小正方体,所以长方体的体积是12cm3. (2) 通过观察发现:小正方体的总个数可以用长方体的长×宽×高迅速求出,所以推得长方体的体积=长×宽×高,用字母表示是:V=abh.
故答案为:(1)12;12cm3;(2)长;宽;高;长;宽;高;V=abh. 【分析】(1)观察图可知,图中的长方体是由棱长为1cm的小正方体搭成的,每个小正方体的体积是1cm3 , 数一数用了几个小正方体,这个长方体的体积就是几立方厘米; (2)观察可以发现:小正方体的总个数可以用长方体的长×宽×高迅速求出,所以推得长方体的体积=长×宽×高,用字母表示是:V=abh,据此解答.
六、应用题
21.【答案】 解:设水深为x分米.
5×5×x=5×4×3 ?? ???????? x=60÷25 ???????? x=2.4
或:5×4×3÷(5×5)=2.4(分米) 答:水深24分米。
【解析】【分析】长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,设水深x分米,根据水的体积相等列出方程,解方程求出水深;用水的体积除以水箱的底面积也可以求出水深。
22.【答案】解:①8×6×5=240(立方分米),240立方分米=240升
②8×6×(5-1.5)=48×3.5=168(立方分米)
或240-8×6×1.5=240-72=168(立方分米)
③(8×6+6×5+5×8)×2 =(48+30+40)×2 =118×2 =236(平方分米) 答:①这个水箱的容积是240升;②水箱内水的体积是168立方分米;③至少需要236平方分米的铁皮。
【解析】【分析】①用水箱的长乘宽乘高求出容积;②用长方体的底面积乘水面的高度求出水的体积;③长方体表面积=(长×宽+长×高+宽×高)×2,根据表面积公式计算。
