五年级下册数学一课一练4.长方体(二)北师大版(含答案)
文档属性
| 名称 | 五年级下册数学一课一练4.长方体(二)北师大版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 59.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-27 12:37:15 | ||
图片预览


文档简介
五年级下册数学一课一练-4.长方体(二)
一、单选题
1.一个水壶能装多少水,是就它的以下哪个数据而言的(?? )。
A.?表面积????????????????????????????????????????B.?体积????????????????????????????????????????C.?容积
2.冰箱的体积( ????)它的容积。
A.大于 B.小于 C.等于
3.运动员领奖台所占空间的大小,就是这个领奖台的(?? )
A.?体积????????????????????????????????????????B.?容积????????????????????????????????????????C.?表面积
4.一个正方体的表面积是24平方厘米,它的体积是(?? )
A.?64平方厘米??????????????????????????????B.?216立方厘米??????????????????????????????C.?8立方厘米
5.底面周长和高分别相等的长方体、正方体和圆柱体,体积最大的是(??? )
A.?长方体??????????????????????????????????????B.?正方体??????????????????????????????????????C.?圆柱体
6.把1升的水倒入容量为200毫升的纸杯中,可以倒(???? )杯。
A.?1?????????????????????????????????????????????B.?5?????????????????????????????????????????????C.?200
二、判断题
7.水杯中装了半杯牛奶,牛奶的体积就是水杯的容积。( ??)
8.判断棱长之和相等的两个正方体,它们的体积相等.
9.体积相等的两个长方体,表面积也一定相等。
10.体积相同的两个长方体,它们的表面积一定也相同。(??? )
11.一个正方体的木箱,体积等于容积.
三、填空题
12.0.4立方米=________立方分米 1.2立方分米=________立方厘米
13.长方体体积计算的字母公式是________,正方体体积计算的字母公式是________.
14.把4个边长是1dm的正方体拼成一个长方体(如图),长方体的表面积是________dm2 , 体积是________dm3。
15.一个长方体的体积是73.2cm3 , 底面积是30cm2 , 高是________cm。
16.0.05L=________cm3;320mL=________dm3
17.一种长方体的砖,长25厘米,宽12.5厘米,厚5厘米。200块这样的砖体积是________立方厘米,合________立方分米。
18.?????
(1)4.2 =________?
(2)1.7 =________?
四、计算题
19.如果我们每人每次在洗漱时浪费1ml水,那么按我国13亿人计算,每人每天洗漱两次,一天可浪费多少水?
五、解答题
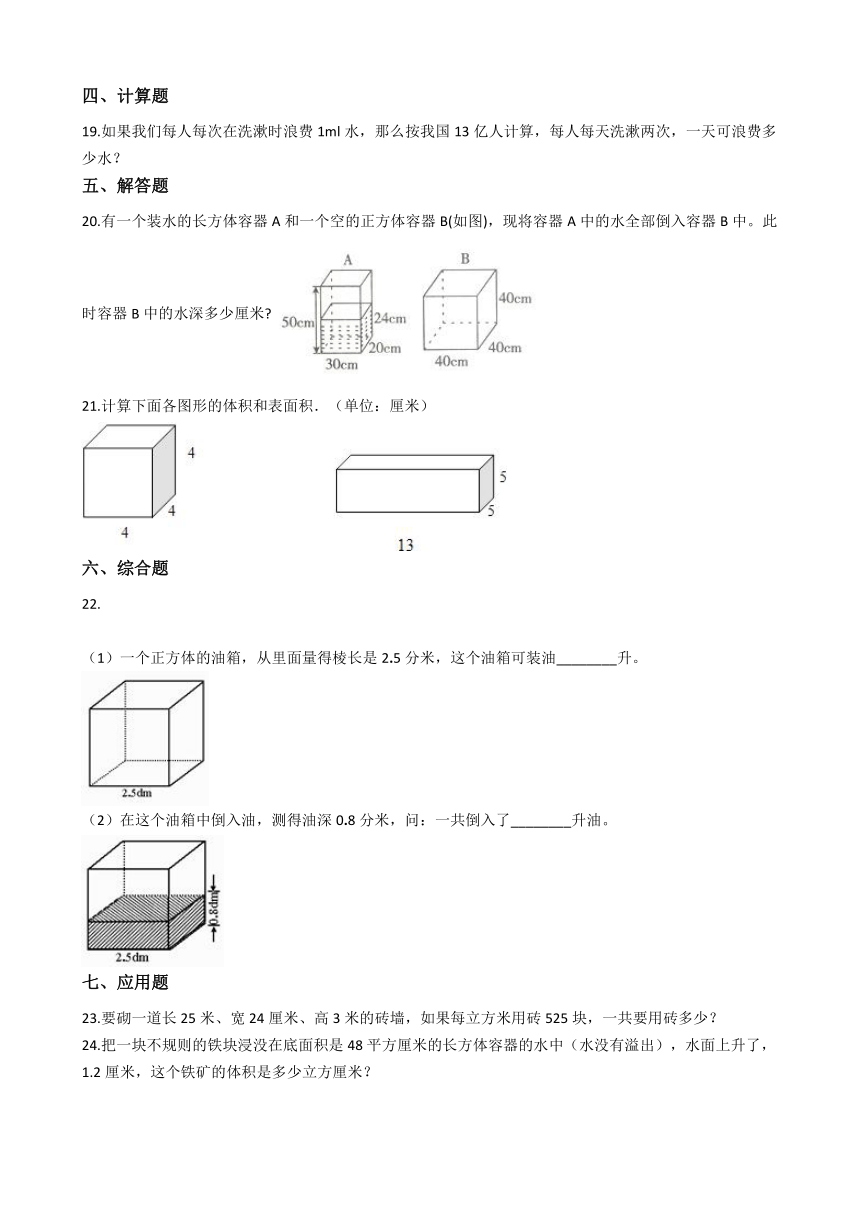
20.有一个装水的长方体容器A和一个空的正方体容器B(如图),现将容器A中的水全部倒入容器B中。此时容器B中的水深多少厘米?
21.计算下面各图形的体积和表面积.(单位:厘米)
六、综合题
22.???????????????????
(1)一个正方体的油箱,从里面量得棱长是2.5分米,这个油箱可装油________升。
(2)在这个油箱中倒入油,测得油深0.8分米,问:一共倒入了________升油。
七、应用题
23.要砌一道长25米、宽24厘米、高3米的砖墙,如果每立方米用砖525块,一共要用砖多少?
24.把一块不规则的铁块浸没在底面积是48平方厘米的长方体容器的水中(水没有溢出),水面上升了,1.2厘米,这个铁矿的体积是多少立方厘米?
答案解析部分
一、单选题
1.【答案】 C
【解析】【解答】水壶能装多少水,算的是水壶所能容纳物体的体积,叫做它的容积,容积是不计算容器的厚度;
【分析】箱子、油桶、仓库等所能容纳物体的体积,通常叫做它们的容积。
2.【答案】 A
【解析】【解答】 冰箱的体积大于它的容积. 故答案为:A. 【分析】物体所占空间的大小叫它的体积,容器所能容纳物体的多少叫它的容积,体积从外面测量数据,容积从里面测量数据,通常一个容器的体积大于它的容积,据此解答.
3.【答案】 A
【解析】【解答】运动员领奖台所占空间的大小,是其所占空间的部分,故选A。
【分析】虽然不同运动会的领奖台的形状可能多种多样,但都是求其所占空间。
4.【答案】 C
【解析】【解答】24÷6=4(平方厘米) 因为2×2=4,所以正方体的棱长是2厘米, 2×2×2 =4×2 =8(立方厘米) 故答案为:C.
【分析】已知正方体的表面积,用正方体的表面积÷6=正方体一个面的面积,然后求出正方体的棱长,最后用公式:正方体的体积=棱长×棱长×棱长,据此列式解答.
5.【答案】 C
【解析】【解答】解:因为圆柱的底面周长=长方体的底面周长=正方体的底面周长,
所以圆柱的底面积>正方体的底面积>长方体的底面积,
又知它们的高相等,所以圆柱的体积>正方体的体积>长方体的体积.
答:底面周长和高分别相等的长方体、正方体和圆柱体,体积最大的是圆柱.
故选:C.
【分析】根据底面周长相等的长方形、正方形、圆形,其中圆的面积最大,因为底面周长和高分别相等的长方体、正方体和圆柱体,而圆柱体的底面积最大,根据圆柱、长方体、正方体的体积=底面积×高,所以圆柱的体积最大.据此解答.
6.【答案】 B
【解析】【解答】解:1L=1000mL,1000÷200=5(杯) 故答案为:B
【分析】1L=1000mL,用1000除以200即可求出可以倒的杯子数.
二、判断题
7.【答案】 错误
【解析】【解答】 水杯中装了半杯牛奶,牛奶的体积小于水杯的容积,原题说法错误. 故答案为:错误. 【分析】箱子、油桶、仓库等所能容纳物体的体积,通常叫做它们的容积,因为水杯里的牛奶没有装满,所以牛奶的体积小于水杯的容积,据此判断.
8.【答案】正确
【解析】【解答】根据分析可知,棱长之和相等的两个正方体,它们的体积相等,原题说法正确. 故答案为:正确. 【分析】正方体的棱长总和=棱长×12,棱长之和相等的两个正方体,它们的棱长相等,由正方体的体积=棱长×棱长×棱长,则它们的体积也相等.
9.【答案】错误
【解析】【解答】假设两个长方体的体积都是24立方厘米,一个长方体的长是6厘米,宽是4厘米,高是1厘米,另一个长方体的的长是8厘米,宽是3厘米,高是1厘米,两个长方体的表面积分别是:642+412+612=68平方厘米,832+812+312=70平方厘米,两个长方体的表面积不相等。 故答案为:错误【分析】假设两个长方体的体积都是24立方厘米,根据两个长方体的体积分别算出两个长方体的长、宽、高分别是多少,再根据长方体的表面积计算公式分别算出两个长方体的表面积,再进行比较即可得到答案。
10.【答案】错误
【解析】【解答】解:如长宽高分别为2、4、6的长方体体积为48,表面积为88;长宽高分别为2、2、12的长方体体积为48,表面积为104. 故表面积相等的两个长方体,它们的体积不一定相等,题干的说法是正确的. 故答案为:错误。【分析】可以举出体积相等的两个长方体,但表面积不相等的反例,继而得出结论.
11.【答案】错误
【解析】【解答】一个正方体的木箱,体积大于容积,原题说法错误. 故答案为:错误. 【分析】正方体木箱的体积是从外面量它的长、宽、高,正方体木箱的容积是从里面量它的长、宽、高,据此解答.
三、填空题
12.【答案】400;1200
【解析】【解答】0.4立方米=0.4×1000=400立方分米 1.2立方分米=1.2×1000=1200立方厘米 故答案为:400;1200. 【分析】1立方分米=1000立方厘米,1立方米=1000立方分米,根据高级单位的数×进率=低级单位的数,低级单位的数÷进率=高级单位的数,据此列式解答.
13.【答案】V=bh;
【解析】【解答】解:长方体体积计算的字母公式是V=abh,正方体体积计算的字母公式是:V=a3。 故答案为:V=abh;V=a3。
【分析】长方体体积=长×宽×高,长用字母a表示,宽用b表示,高用h表示,V表示体积;正方体体积=棱长×棱长×棱长,棱长用字母a表示。
14.【答案】18;4
【解析】【解答】解:4×1×4+1×1×2 =16+2 =18(dm2) 体积:4×1×1=4(dm3)。 故答案为:18;4【分析】先判断拼成的长方体的长,然后根据长方体表面积公式计算表面积,用长乘宽乘高求出体积即可。
15.【答案】2.44
【解析】【解答】解:73.2÷30=2.44(cm) 故答案为:2.44【分析】长方体的体积=底面积×高,由此用长方体的体积除以底面积即可求出高。
16.【答案】50;0.32
【解析】【解答】解:0.05×1000=50,所以0.05L=50cm3; 320÷1000=0.32,所以320mL=0.32dm3 故答案为:50;0.32
【分析】1L=1000cm3,1dm3=1000mL,把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率.
17.【答案】312500;312.5
【解析】【解答】解:25×12.5×5×200 =312.5×1000 =312500(立方厘米) 312500立方厘米=312.5立方分米 故答案为:312500;312.5 【分析】长方体体积=长×宽×高,根据长方体体积公式计算一块砖的体积,再乘200就是总体积,然后换算单位,1立方分米=1000立方厘米.
18.【答案】 (1)420 (2)170
【解析】【解答】解:(1)4.2×100=420,所以4.2m2=420dm2; (2)1.7×1000=1700,所以1.7m3=1700dm3。 故答案为:(1)420;(2)1700。
【分析】(1)1m2=100dm2,把m2换算成dm2要乘进率100; (2)1m3=1000dm3,把m3换算成dm3要乘进率1000。
四、计算题
19.【答案】 解:1300000000×1×2=2600000000(ml)
2600000000ml=2600m3 答:一天可浪费2600m3水。
【解析】【解答】 1300000000×1×2 =1300000000×2 =2600000000(ml) 2600000000ml=2600m3 答:一天可浪费2600m3水。
【分析】13亿=1300000000,先用乘法求出13亿人每次洗漱浪费水的体积,然后乘2即可得到13亿人一天洗漱两次浪费的水的体积,然后把体积单位毫升化成立方米,除以进率1000000,据此解答即可.
五、解答题
20.【答案】解:30×20×24÷(40×40) =14400÷1600 =9(厘米) 答:此时容器B中的水深9厘米.
【解析】【分析】长方体体积=长×宽×高,根据长方体体积计算出A容器中水的体积,然后除以B容器的底面积即可求出水深.
21.【答案】解:1)正方体的体积:4×4×4 =16×4 =64(立方厘米) 表面积:6×4×4 =24×4 =96(平方厘米) 答:正方体的体积是64平方厘米,表面积是96平方厘米. 2)长方体的体积:13×5×5 =65×5 =325(立方厘米) 表面积:(13×5+13×5+5×5)×2 =(65+65+25)×2 =155×2 =310(平方厘米) 答:长方体的体积是325立方厘米,表面积是310平方厘米
【解析】【分析】(1)正方体的体积V=a3 , 表面积S=6a2 , 正方体的棱长已知,代入公式即可求解;(2)长方体的体积V=abh,表面积S=(ab+bh+ah)×2,代入公式即可求解.
六、综合题
22.【答案】(1)15.625 (2)5
【解析】【解答】解:(1)2.5×2.5×2.5=15.625(升) (2)2.5×2.5×0.8 =6.25×0.8 =5(升) 故答案为:15.625;5
【分析】(1)根据正方体体积公式计算容积即可;(2)用油箱的底面积乘油的高度即可求出油的体积.
七、应用题
23.【答案】525×(25×0.24×3) =525×(6×3) =525×18 =9450(块) 答:一共要用砖9450块.
【解析】【分析】根据题意可知,先求出这个长方体砖墙的体积,用长×宽×高=长方体砖墙的体积,然后用每立方米用砖数量×长方体砖墙的体积=用砖总数量,据此解答.
24.【答案】解:48×1.2=57.6(立方厘米) 答:这个铁矿的体积是57.6立方厘米.
【解析】【分析】水面上升部分水的体积就是铁矿的体积,由此用底面积乘水面上升的高度就是铁矿的体积.
一、单选题
1.一个水壶能装多少水,是就它的以下哪个数据而言的(?? )。
A.?表面积????????????????????????????????????????B.?体积????????????????????????????????????????C.?容积
2.冰箱的体积( ????)它的容积。
A.大于 B.小于 C.等于
3.运动员领奖台所占空间的大小,就是这个领奖台的(?? )
A.?体积????????????????????????????????????????B.?容积????????????????????????????????????????C.?表面积
4.一个正方体的表面积是24平方厘米,它的体积是(?? )
A.?64平方厘米??????????????????????????????B.?216立方厘米??????????????????????????????C.?8立方厘米
5.底面周长和高分别相等的长方体、正方体和圆柱体,体积最大的是(??? )
A.?长方体??????????????????????????????????????B.?正方体??????????????????????????????????????C.?圆柱体
6.把1升的水倒入容量为200毫升的纸杯中,可以倒(???? )杯。
A.?1?????????????????????????????????????????????B.?5?????????????????????????????????????????????C.?200
二、判断题
7.水杯中装了半杯牛奶,牛奶的体积就是水杯的容积。( ??)
8.判断棱长之和相等的两个正方体,它们的体积相等.
9.体积相等的两个长方体,表面积也一定相等。
10.体积相同的两个长方体,它们的表面积一定也相同。(??? )
11.一个正方体的木箱,体积等于容积.
三、填空题
12.0.4立方米=________立方分米 1.2立方分米=________立方厘米
13.长方体体积计算的字母公式是________,正方体体积计算的字母公式是________.
14.把4个边长是1dm的正方体拼成一个长方体(如图),长方体的表面积是________dm2 , 体积是________dm3。
15.一个长方体的体积是73.2cm3 , 底面积是30cm2 , 高是________cm。
16.0.05L=________cm3;320mL=________dm3
17.一种长方体的砖,长25厘米,宽12.5厘米,厚5厘米。200块这样的砖体积是________立方厘米,合________立方分米。
18.?????
(1)4.2 =________?
(2)1.7 =________?
四、计算题
19.如果我们每人每次在洗漱时浪费1ml水,那么按我国13亿人计算,每人每天洗漱两次,一天可浪费多少水?
五、解答题
20.有一个装水的长方体容器A和一个空的正方体容器B(如图),现将容器A中的水全部倒入容器B中。此时容器B中的水深多少厘米?
21.计算下面各图形的体积和表面积.(单位:厘米)
六、综合题
22.???????????????????
(1)一个正方体的油箱,从里面量得棱长是2.5分米,这个油箱可装油________升。
(2)在这个油箱中倒入油,测得油深0.8分米,问:一共倒入了________升油。
七、应用题
23.要砌一道长25米、宽24厘米、高3米的砖墙,如果每立方米用砖525块,一共要用砖多少?
24.把一块不规则的铁块浸没在底面积是48平方厘米的长方体容器的水中(水没有溢出),水面上升了,1.2厘米,这个铁矿的体积是多少立方厘米?
答案解析部分
一、单选题
1.【答案】 C
【解析】【解答】水壶能装多少水,算的是水壶所能容纳物体的体积,叫做它的容积,容积是不计算容器的厚度;
【分析】箱子、油桶、仓库等所能容纳物体的体积,通常叫做它们的容积。
2.【答案】 A
【解析】【解答】 冰箱的体积大于它的容积. 故答案为:A. 【分析】物体所占空间的大小叫它的体积,容器所能容纳物体的多少叫它的容积,体积从外面测量数据,容积从里面测量数据,通常一个容器的体积大于它的容积,据此解答.
3.【答案】 A
【解析】【解答】运动员领奖台所占空间的大小,是其所占空间的部分,故选A。
【分析】虽然不同运动会的领奖台的形状可能多种多样,但都是求其所占空间。
4.【答案】 C
【解析】【解答】24÷6=4(平方厘米) 因为2×2=4,所以正方体的棱长是2厘米, 2×2×2 =4×2 =8(立方厘米) 故答案为:C.
【分析】已知正方体的表面积,用正方体的表面积÷6=正方体一个面的面积,然后求出正方体的棱长,最后用公式:正方体的体积=棱长×棱长×棱长,据此列式解答.
5.【答案】 C
【解析】【解答】解:因为圆柱的底面周长=长方体的底面周长=正方体的底面周长,
所以圆柱的底面积>正方体的底面积>长方体的底面积,
又知它们的高相等,所以圆柱的体积>正方体的体积>长方体的体积.
答:底面周长和高分别相等的长方体、正方体和圆柱体,体积最大的是圆柱.
故选:C.
【分析】根据底面周长相等的长方形、正方形、圆形,其中圆的面积最大,因为底面周长和高分别相等的长方体、正方体和圆柱体,而圆柱体的底面积最大,根据圆柱、长方体、正方体的体积=底面积×高,所以圆柱的体积最大.据此解答.
6.【答案】 B
【解析】【解答】解:1L=1000mL,1000÷200=5(杯) 故答案为:B
【分析】1L=1000mL,用1000除以200即可求出可以倒的杯子数.
二、判断题
7.【答案】 错误
【解析】【解答】 水杯中装了半杯牛奶,牛奶的体积小于水杯的容积,原题说法错误. 故答案为:错误. 【分析】箱子、油桶、仓库等所能容纳物体的体积,通常叫做它们的容积,因为水杯里的牛奶没有装满,所以牛奶的体积小于水杯的容积,据此判断.
8.【答案】正确
【解析】【解答】根据分析可知,棱长之和相等的两个正方体,它们的体积相等,原题说法正确. 故答案为:正确. 【分析】正方体的棱长总和=棱长×12,棱长之和相等的两个正方体,它们的棱长相等,由正方体的体积=棱长×棱长×棱长,则它们的体积也相等.
9.【答案】错误
【解析】【解答】假设两个长方体的体积都是24立方厘米,一个长方体的长是6厘米,宽是4厘米,高是1厘米,另一个长方体的的长是8厘米,宽是3厘米,高是1厘米,两个长方体的表面积分别是:642+412+612=68平方厘米,832+812+312=70平方厘米,两个长方体的表面积不相等。 故答案为:错误【分析】假设两个长方体的体积都是24立方厘米,根据两个长方体的体积分别算出两个长方体的长、宽、高分别是多少,再根据长方体的表面积计算公式分别算出两个长方体的表面积,再进行比较即可得到答案。
10.【答案】错误
【解析】【解答】解:如长宽高分别为2、4、6的长方体体积为48,表面积为88;长宽高分别为2、2、12的长方体体积为48,表面积为104. 故表面积相等的两个长方体,它们的体积不一定相等,题干的说法是正确的. 故答案为:错误。【分析】可以举出体积相等的两个长方体,但表面积不相等的反例,继而得出结论.
11.【答案】错误
【解析】【解答】一个正方体的木箱,体积大于容积,原题说法错误. 故答案为:错误. 【分析】正方体木箱的体积是从外面量它的长、宽、高,正方体木箱的容积是从里面量它的长、宽、高,据此解答.
三、填空题
12.【答案】400;1200
【解析】【解答】0.4立方米=0.4×1000=400立方分米 1.2立方分米=1.2×1000=1200立方厘米 故答案为:400;1200. 【分析】1立方分米=1000立方厘米,1立方米=1000立方分米,根据高级单位的数×进率=低级单位的数,低级单位的数÷进率=高级单位的数,据此列式解答.
13.【答案】V=bh;
【解析】【解答】解:长方体体积计算的字母公式是V=abh,正方体体积计算的字母公式是:V=a3。 故答案为:V=abh;V=a3。
【分析】长方体体积=长×宽×高,长用字母a表示,宽用b表示,高用h表示,V表示体积;正方体体积=棱长×棱长×棱长,棱长用字母a表示。
14.【答案】18;4
【解析】【解答】解:4×1×4+1×1×2 =16+2 =18(dm2) 体积:4×1×1=4(dm3)。 故答案为:18;4【分析】先判断拼成的长方体的长,然后根据长方体表面积公式计算表面积,用长乘宽乘高求出体积即可。
15.【答案】2.44
【解析】【解答】解:73.2÷30=2.44(cm) 故答案为:2.44【分析】长方体的体积=底面积×高,由此用长方体的体积除以底面积即可求出高。
16.【答案】50;0.32
【解析】【解答】解:0.05×1000=50,所以0.05L=50cm3; 320÷1000=0.32,所以320mL=0.32dm3 故答案为:50;0.32
【分析】1L=1000cm3,1dm3=1000mL,把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率.
17.【答案】312500;312.5
【解析】【解答】解:25×12.5×5×200 =312.5×1000 =312500(立方厘米) 312500立方厘米=312.5立方分米 故答案为:312500;312.5 【分析】长方体体积=长×宽×高,根据长方体体积公式计算一块砖的体积,再乘200就是总体积,然后换算单位,1立方分米=1000立方厘米.
18.【答案】 (1)420 (2)170
【解析】【解答】解:(1)4.2×100=420,所以4.2m2=420dm2; (2)1.7×1000=1700,所以1.7m3=1700dm3。 故答案为:(1)420;(2)1700。
【分析】(1)1m2=100dm2,把m2换算成dm2要乘进率100; (2)1m3=1000dm3,把m3换算成dm3要乘进率1000。
四、计算题
19.【答案】 解:1300000000×1×2=2600000000(ml)
2600000000ml=2600m3 答:一天可浪费2600m3水。
【解析】【解答】 1300000000×1×2 =1300000000×2 =2600000000(ml) 2600000000ml=2600m3 答:一天可浪费2600m3水。
【分析】13亿=1300000000,先用乘法求出13亿人每次洗漱浪费水的体积,然后乘2即可得到13亿人一天洗漱两次浪费的水的体积,然后把体积单位毫升化成立方米,除以进率1000000,据此解答即可.
五、解答题
20.【答案】解:30×20×24÷(40×40) =14400÷1600 =9(厘米) 答:此时容器B中的水深9厘米.
【解析】【分析】长方体体积=长×宽×高,根据长方体体积计算出A容器中水的体积,然后除以B容器的底面积即可求出水深.
21.【答案】解:1)正方体的体积:4×4×4 =16×4 =64(立方厘米) 表面积:6×4×4 =24×4 =96(平方厘米) 答:正方体的体积是64平方厘米,表面积是96平方厘米. 2)长方体的体积:13×5×5 =65×5 =325(立方厘米) 表面积:(13×5+13×5+5×5)×2 =(65+65+25)×2 =155×2 =310(平方厘米) 答:长方体的体积是325立方厘米,表面积是310平方厘米
【解析】【分析】(1)正方体的体积V=a3 , 表面积S=6a2 , 正方体的棱长已知,代入公式即可求解;(2)长方体的体积V=abh,表面积S=(ab+bh+ah)×2,代入公式即可求解.
六、综合题
22.【答案】(1)15.625 (2)5
【解析】【解答】解:(1)2.5×2.5×2.5=15.625(升) (2)2.5×2.5×0.8 =6.25×0.8 =5(升) 故答案为:15.625;5
【分析】(1)根据正方体体积公式计算容积即可;(2)用油箱的底面积乘油的高度即可求出油的体积.
七、应用题
23.【答案】525×(25×0.24×3) =525×(6×3) =525×18 =9450(块) 答:一共要用砖9450块.
【解析】【分析】根据题意可知,先求出这个长方体砖墙的体积,用长×宽×高=长方体砖墙的体积,然后用每立方米用砖数量×长方体砖墙的体积=用砖总数量,据此解答.
24.【答案】解:48×1.2=57.6(立方厘米) 答:这个铁矿的体积是57.6立方厘米.
【解析】【分析】水面上升部分水的体积就是铁矿的体积,由此用底面积乘水面上升的高度就是铁矿的体积.
