2018_2019学年高中数学第二章数列2.4等比数列第1课时等比数列的概念与通项公式课件新人教A版必修5(35张PPT)
文档属性
| 名称 | 2018_2019学年高中数学第二章数列2.4等比数列第1课时等比数列的概念与通项公式课件新人教A版必修5(35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-26 20:49:35 | ||
图片预览









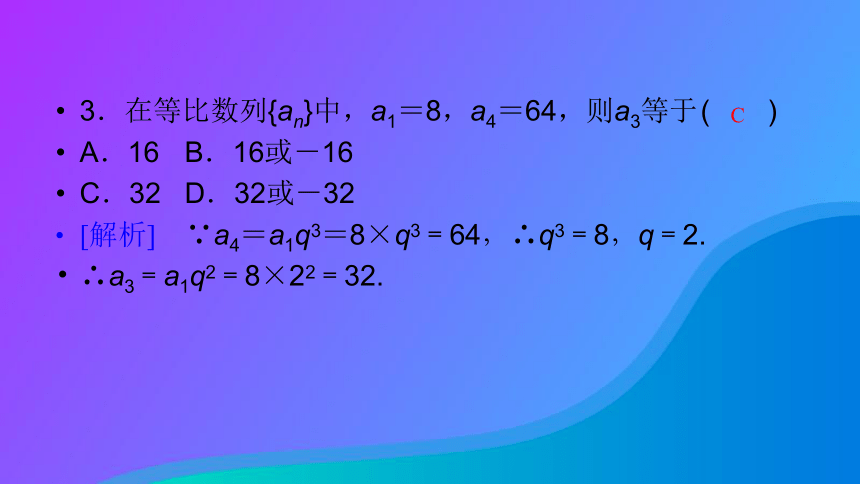
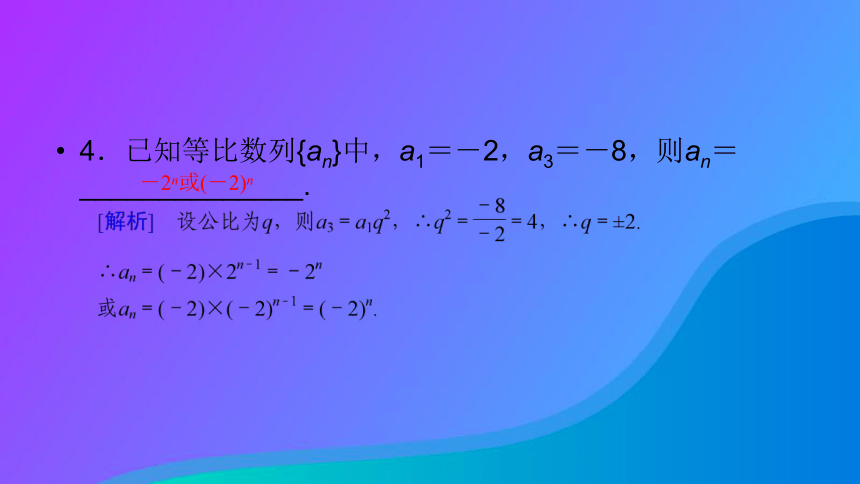

文档简介
课件35张PPT。第 二 章数列2.4 等比数列第1课时 等比数列的概念与通项公式自主预习学案我们古代数学名著《孙子算经》中有一个有趣的问题叫“出门望九堤”:“今有出门望九堤,堤有九木,木有九枝,枝有九巢,巢有九禽,禽有九雏,雏有九毛,毛有九色,问各有几何?”上述问题中的各种东西的数量构成了怎样的数列?
1.等比数列的定义
如果一个数列从_________起,每一项与它的前一项的比都等于______________,那么这个数列叫做等比数列,这个常数叫做等比数列的________,公比通常用字母______表示.
第2项 同一个常数 公比 q 2.等比数列的递推公式与通项公式
已知等比数列{an}的首项为a1,公比为 q(q≠0),
填表:3.等比中项
(1)如果三个数x,G,y组成____________,则G叫做x和y的等比中项.
(2)如果G是x和y的等比中项,那么___________,即____________.q a1qn-1 等比数列 G2=xy B
2.下列说法:①公差为0的等差数列是等比数列;②b2=ac,则a,b,c成等比数列;③2b=a+c,则a,b,c成等差数列;④任意两项都有等比中项.正确的有 ( )
A.① B.③
C.①③ D.②④
[解析] 公差为0的非零数列是等比数列,故①不正确,②中只有a,b,c都不为0才正确,④只有同号的两项才有等比中项,∴只有③正确.
B
3.在等比数列{an}中,a1=8,a4=64,则a3等于 ( )
A.16 B.16或-16
C.32 D.32或-32
[解析] ∵a4=a1q3=8×q3=64,∴q3=8,q=2.
∴a3=a1q2=8×22=32.
C 4.已知等比数列{an}中,a1=-2,a3=-8,则an=______________.-2n或(-2)n 5.若等比数列{an}满足anan+1=16n,求公比q的值.互动探究学案命题方向1 ?等比数列的通项公式 已知等比数列{an},若a1+a2+a3=7,a1a2a3=8,求an.
[分析] (1)在等比数列的通项公式中含有两个待定系数a1和q,故需建立a1与q的两个方程,组成方程组求解,因此只需将已知条件改写成a1与q的关系式即可.
(2)由等比中项的定义知,a2是a1与a3的等比中项,故可先由a1a2a3=8求得a2,再解关于a1与a3的方程组,即可获解.例题 1『规律总结』 求等比数列的通项公式与求等差数列的通项公式一样,运用方程的思想,建立基本量的方程(或方程组)求解,在a1,an,n,q四个量中,已知三个可求另一个.〔跟踪练习1〕
在等比数列{an}中,
(1)a4=2,a7=8,求an;
(2)a2+a5=18,a3+a6=9,an=1,求n.命题方向2 ?等比数列的判定与证明 已知数列{an}满足a1=1,an+1=2an+1,bn=an+1(n∈N*).
(1)求证{bn}是等比数列;
(2)求{an}的通项公式.例题 2
〔跟踪练习2〕
数列{an}满足a1=-1,且an=3an-1-2n+3(n∈N*,且n≥2).
(1)求a2,a3,并证明数列{an-n}是等比数列;
(2)求数列{an}的通项公式.命题方向3 ?等比中项 等差数列{an}的公差不为零,首项a1=1,a2是a1和a5的等比中项,则数列{an}的前10项之和是 ( )
A.90 B.100
C.145 D.190例题 3B 『规律总结』 等比中项的应用主要有两点:①计算,与其它性质综合应用,起到简化计算、提高解题速度的作用.②用来判断或证明等比数列.〔跟踪练习3〕
在等比数列{an}中,a5,a9是方程7x2-18x+7=0的两个根,则a7=_____.1 等比数列{an}的前三项的和为168,a2-a5=42,求a5、a7的等比中项.例题 4忽视等比中项的符号致错 [辨析] 错误的原因在于认为a5,a7的等比中项是a6,忽略了同号两数的等比中项有两个且互为相反数. 某人买了一辆价值13.5万元的新车,专家预测这种车每年按10%的速度贬值.
(1)用一个式子表示第n(n∈N+)年这辆车的价值;
(2)如果他打算用满4年时卖掉这辆车,他大概能得到多少钱?
[分析] 根据题意,每年车的价值存在倍数关系,所以能建立等比数列模型来解决.例题 5数列的实际应用问题 [解析] (1)从第一年起,每年车的价值(万元)依次设为:a1,a2,a3,…,an,
由题意,得a1=13.5,a2=13.5(1-10%),a3=13.5(1-10%)2,….
由等比数列定义知数列{an}是等比数列,首项a1=13.5,公比q=(1-10%)=0.9,
∴an=a1·qn-1=13.5×(0.9)n-1.∴第n年车的价值为an=13.5×(0.9)n-1万元.
(2)当他用满4年时,车的价值为a5=13.5×(0.9)5-1=8.857.
∴用满4年卖掉时,他大概能得8.857万元.『规律总结』 解答数列实际应用问题的一般思路
(1)建模:根据题设条件,建立数列模型:①分析实际问题的结构特征;②找出所含元素的数量关系;③确定为何种数列模型;
(2)解模:利用相关的数列知识加以解决:①分清首项、公差、项数等;②分清是an还是Sn问题;③选用适当的方法求解;
(3)还原:把数学问题的解还原为实际问题,针对实际问题的约束条件合理修正,使其成为实际问题的解.
1.已知等比数列{an}满足a1+a2=3,a2+a3=6,则a7等于 ( )
A.64 B.81
C.128 D.243
[解析] 设等比数列的公比为q,
∵a1+a2=3,a2+a3=q(a1+a2)=6,∴q=2.
又a1+a2=a1+a1q=3,∴3a1=3.∴a1=1,∴a7=26=64.A
2.在等比数列{an}中,a3+a4=4,a2=2,则公比q等于 ( )
A.-2 B.1或-2
C.1 D.1或2
[解析] ∵在等比数列{an}中,a3+a4=4,a2=2,∴a3+a4=a2q+a2q2=2q+2q2=4,即q2+q-2=0.解得q=1或q=-2.故选B.B 4
1.等比数列的定义
如果一个数列从_________起,每一项与它的前一项的比都等于______________,那么这个数列叫做等比数列,这个常数叫做等比数列的________,公比通常用字母______表示.
第2项 同一个常数 公比 q 2.等比数列的递推公式与通项公式
已知等比数列{an}的首项为a1,公比为 q(q≠0),
填表:3.等比中项
(1)如果三个数x,G,y组成____________,则G叫做x和y的等比中项.
(2)如果G是x和y的等比中项,那么___________,即____________.q a1qn-1 等比数列 G2=xy B
2.下列说法:①公差为0的等差数列是等比数列;②b2=ac,则a,b,c成等比数列;③2b=a+c,则a,b,c成等差数列;④任意两项都有等比中项.正确的有 ( )
A.① B.③
C.①③ D.②④
[解析] 公差为0的非零数列是等比数列,故①不正确,②中只有a,b,c都不为0才正确,④只有同号的两项才有等比中项,∴只有③正确.
B
3.在等比数列{an}中,a1=8,a4=64,则a3等于 ( )
A.16 B.16或-16
C.32 D.32或-32
[解析] ∵a4=a1q3=8×q3=64,∴q3=8,q=2.
∴a3=a1q2=8×22=32.
C 4.已知等比数列{an}中,a1=-2,a3=-8,则an=______________.-2n或(-2)n 5.若等比数列{an}满足anan+1=16n,求公比q的值.互动探究学案命题方向1 ?等比数列的通项公式 已知等比数列{an},若a1+a2+a3=7,a1a2a3=8,求an.
[分析] (1)在等比数列的通项公式中含有两个待定系数a1和q,故需建立a1与q的两个方程,组成方程组求解,因此只需将已知条件改写成a1与q的关系式即可.
(2)由等比中项的定义知,a2是a1与a3的等比中项,故可先由a1a2a3=8求得a2,再解关于a1与a3的方程组,即可获解.例题 1『规律总结』 求等比数列的通项公式与求等差数列的通项公式一样,运用方程的思想,建立基本量的方程(或方程组)求解,在a1,an,n,q四个量中,已知三个可求另一个.〔跟踪练习1〕
在等比数列{an}中,
(1)a4=2,a7=8,求an;
(2)a2+a5=18,a3+a6=9,an=1,求n.命题方向2 ?等比数列的判定与证明 已知数列{an}满足a1=1,an+1=2an+1,bn=an+1(n∈N*).
(1)求证{bn}是等比数列;
(2)求{an}的通项公式.例题 2
〔跟踪练习2〕
数列{an}满足a1=-1,且an=3an-1-2n+3(n∈N*,且n≥2).
(1)求a2,a3,并证明数列{an-n}是等比数列;
(2)求数列{an}的通项公式.命题方向3 ?等比中项 等差数列{an}的公差不为零,首项a1=1,a2是a1和a5的等比中项,则数列{an}的前10项之和是 ( )
A.90 B.100
C.145 D.190例题 3B 『规律总结』 等比中项的应用主要有两点:①计算,与其它性质综合应用,起到简化计算、提高解题速度的作用.②用来判断或证明等比数列.〔跟踪练习3〕
在等比数列{an}中,a5,a9是方程7x2-18x+7=0的两个根,则a7=_____.1 等比数列{an}的前三项的和为168,a2-a5=42,求a5、a7的等比中项.例题 4忽视等比中项的符号致错 [辨析] 错误的原因在于认为a5,a7的等比中项是a6,忽略了同号两数的等比中项有两个且互为相反数. 某人买了一辆价值13.5万元的新车,专家预测这种车每年按10%的速度贬值.
(1)用一个式子表示第n(n∈N+)年这辆车的价值;
(2)如果他打算用满4年时卖掉这辆车,他大概能得到多少钱?
[分析] 根据题意,每年车的价值存在倍数关系,所以能建立等比数列模型来解决.例题 5数列的实际应用问题 [解析] (1)从第一年起,每年车的价值(万元)依次设为:a1,a2,a3,…,an,
由题意,得a1=13.5,a2=13.5(1-10%),a3=13.5(1-10%)2,….
由等比数列定义知数列{an}是等比数列,首项a1=13.5,公比q=(1-10%)=0.9,
∴an=a1·qn-1=13.5×(0.9)n-1.∴第n年车的价值为an=13.5×(0.9)n-1万元.
(2)当他用满4年时,车的价值为a5=13.5×(0.9)5-1=8.857.
∴用满4年卖掉时,他大概能得8.857万元.『规律总结』 解答数列实际应用问题的一般思路
(1)建模:根据题设条件,建立数列模型:①分析实际问题的结构特征;②找出所含元素的数量关系;③确定为何种数列模型;
(2)解模:利用相关的数列知识加以解决:①分清首项、公差、项数等;②分清是an还是Sn问题;③选用适当的方法求解;
(3)还原:把数学问题的解还原为实际问题,针对实际问题的约束条件合理修正,使其成为实际问题的解.
1.已知等比数列{an}满足a1+a2=3,a2+a3=6,则a7等于 ( )
A.64 B.81
C.128 D.243
[解析] 设等比数列的公比为q,
∵a1+a2=3,a2+a3=q(a1+a2)=6,∴q=2.
又a1+a2=a1+a1q=3,∴3a1=3.∴a1=1,∴a7=26=64.A
2.在等比数列{an}中,a3+a4=4,a2=2,则公比q等于 ( )
A.-2 B.1或-2
C.1 D.1或2
[解析] ∵在等比数列{an}中,a3+a4=4,a2=2,∴a3+a4=a2q+a2q2=2q+2q2=4,即q2+q-2=0.解得q=1或q=-2.故选B.B 4
