2018_2019学年高中数学第二章数列2.4等比数列第2课时等比数列的性质课件新人教A版必修5(40张PPT)
文档属性
| 名称 | 2018_2019学年高中数学第二章数列2.4等比数列第2课时等比数列的性质课件新人教A版必修5(40张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 963.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-26 20:50:51 | ||
图片预览






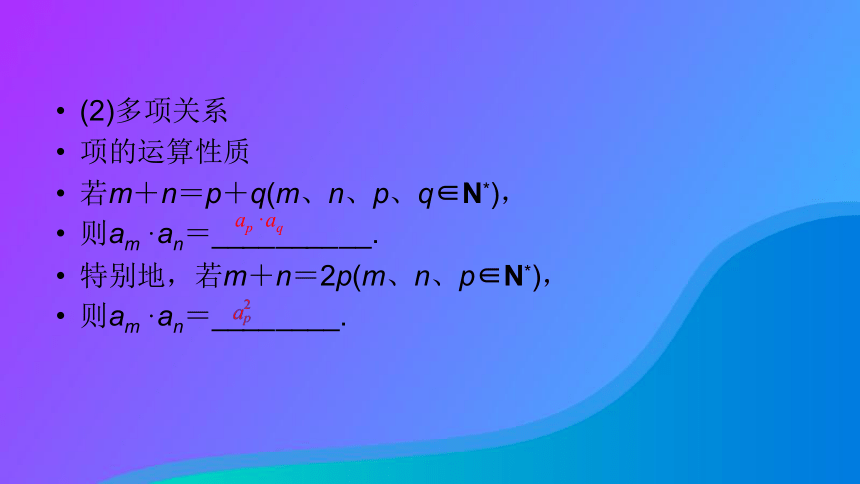





文档简介
课件40张PPT。第 二 章数列2.4 等比数列第2课时 等比数列的性质自主预习学案1915年,波兰数学家谢尔宾斯基(W.Sierpinski)创造了一个美妙的“艺术品”,被人们称为谢尔宾斯基三角形,如图所示.如果我们来看一看图中那些白色三角形的个数,并把它们按面积大小,从小到大依次排列起来,可以得到一列数:1,3,9,27,81,……我们知道,这些数构成等比数列,那么等比数列具有哪些独特的性质呢?
1.等比数列的项与序号的关系
(1)两项关系
通项公式的推广:
an=am·______(m、n∈N*).
qn-m
(2)多项关系
项的运算性质
若m+n=p+q(m、n、p、q∈N*),
则am·an=__________.
特别地,若m+n=2p(m、n、p∈N*),
则am·an=________.ap·aq an-1 an-k+1 cq |q| q1·q2
4.等比数列的单调性
(1)当a1>0,q>1或a1<0,0(2)当a1>0,01时,等比数列{an}为递______数列;
(3)当q=1时,数列{an}是常数列;
(4)当q<0时,数列{an}是摆动数列.增 减
1.等比数列{an}中,a4=4,则a2·a6等于 ( )
A.4 B.8
C.16 D.32
[解析] ∵{an}是等比数列,
∴a2a6=a=42=16.C B 3.已知{an}是等比数列,且an>0,a2a4+2a3a5+a4a6=25,那么a3+a5= ( )
A.5 B.10
C.15 D.20A
4.等比数列{an}中,a1=1,a9=9,则a5=_____.3 互动探究学案命题方向1 ?等比数列的性质 在等比数列{an}中,已知a4a7=-512,a3+a8=124,且公比为整数,则a10=_______.例题 1512
〔跟踪练习1〕
(1)在等比数列{an}中,已知a7a12=5,则a8a9a10a11=______;
(2){an}为等比数列,且a1a9=64,a3+a7=20,则a11=_________;
(3)在等比数列{an}中,若a2·a8=36,a3+a7=15,则公比q值的个数可能为 ( )
A.1个 B.2个
C.3个 D.4个25 1或64 D 命题方向2 ?等比数列的设项技巧 已知四个数前三个成等差,后三个成等比,中间两数之积为16,首尾两个数之积为-128,求这四个数.
[分析] 求四个数,给出四个条件,若列四个方程组成方程组虽可解,但较麻烦,因此可依据条件减少未知数的个数.设未知数时,可以根据前三个数成等差来设,也可以依据后三个数成等比来设,还可以依据中间(或首尾)两数之积来设,关键是要把握住未知量要尽量少,下一步运算要简捷.例题 2
〔跟踪练习2〕
(1)有四个数成等比数列,将这四个数分别减去1,1,4,13,则成等差数列,则这四个数为________________.
(2)三个互不相等的数成等差数列,如果适当排列三个数,又可成为等比数列,这三个数的和为6,则这三个数为_____________.
[分析] (1)四个数成等比数列,可用第一个数与公比q表示各数,然后按所给条件列方程组求解.
(2)三个数适当排列,不同的排列方法有6种,但这里不必分成6种,因为若以三个数中哪一个数为等比中项分类,则只有三种情况,因此对于分类讨论问题,恰当的分类是解决问题的关键.3,6,12,24 -4,2,8 (2)由已知,可设这三个数为a-d,a,a+d,则a-d+a+a+d=6,∴a=2,
这三个数可表示为2-d,2,2+d,
①若2-d为等比中项,则有(2-d)2=2(2+d),解之得d=6,或d=0(舍去).此时三个数为-4,2,8.
②若2+d是等比中项,则有(2+d)2=2(2-d),解之得d=-6,或d=0(舍去).此时三个数为8,2,-4.
③若2为等比中项,则22=(2+d)·(2-d),∴d=0(舍去).
综上可知此三数为-4,2,8.例题 3忽视等比数列中奇数项符号相同、偶数项符号相同而致错 例题 4方程思想在等比数列中的应用 1.已知{an},{bn}都是等比数列,那么 ( )
A.{an+bn},{an·bn}都一定是等比数列
B.{an+bn}一定是等比数列,但{an·bn}不一定是等比数列
C.{an+bn}不一定是等比数列,但{an·bn}一定是等比数列
D.{an+bn},{an·bn}都不一定是等比数列
[解析] 当两个数列都是等比数列时,这两个数列的和不一定是等比数列,比如取两个数列是互为相反数的数列,两者的和就不是等比数列.两个等比数列的积一定是等比数列.C B 3.(2018-2019学年度山东荣成六中高二月考)已知等比数列{an}中,a2+a5=18,a3·a4=32,若an=128,q>1,则n= ( )
A.8 B.7
C.6 D.5A 4.已知等比数列{an}中,a4=7,a6=21,则a12=_______.567 5.已知三个数成等比数列,它们的积为27,它们的平方和为91,求这三个数.
1.等比数列的项与序号的关系
(1)两项关系
通项公式的推广:
an=am·______(m、n∈N*).
qn-m
(2)多项关系
项的运算性质
若m+n=p+q(m、n、p、q∈N*),
则am·an=__________.
特别地,若m+n=2p(m、n、p∈N*),
则am·an=________.ap·aq an-1 an-k+1 cq |q| q1·q2
4.等比数列的单调性
(1)当a1>0,q>1或a1<0,0
(3)当q=1时,数列{an}是常数列;
(4)当q<0时,数列{an}是摆动数列.增 减
1.等比数列{an}中,a4=4,则a2·a6等于 ( )
A.4 B.8
C.16 D.32
[解析] ∵{an}是等比数列,
∴a2a6=a=42=16.C B 3.已知{an}是等比数列,且an>0,a2a4+2a3a5+a4a6=25,那么a3+a5= ( )
A.5 B.10
C.15 D.20A
4.等比数列{an}中,a1=1,a9=9,则a5=_____.3 互动探究学案命题方向1 ?等比数列的性质 在等比数列{an}中,已知a4a7=-512,a3+a8=124,且公比为整数,则a10=_______.例题 1512
〔跟踪练习1〕
(1)在等比数列{an}中,已知a7a12=5,则a8a9a10a11=______;
(2){an}为等比数列,且a1a9=64,a3+a7=20,则a11=_________;
(3)在等比数列{an}中,若a2·a8=36,a3+a7=15,则公比q值的个数可能为 ( )
A.1个 B.2个
C.3个 D.4个25 1或64 D 命题方向2 ?等比数列的设项技巧 已知四个数前三个成等差,后三个成等比,中间两数之积为16,首尾两个数之积为-128,求这四个数.
[分析] 求四个数,给出四个条件,若列四个方程组成方程组虽可解,但较麻烦,因此可依据条件减少未知数的个数.设未知数时,可以根据前三个数成等差来设,也可以依据后三个数成等比来设,还可以依据中间(或首尾)两数之积来设,关键是要把握住未知量要尽量少,下一步运算要简捷.例题 2
〔跟踪练习2〕
(1)有四个数成等比数列,将这四个数分别减去1,1,4,13,则成等差数列,则这四个数为________________.
(2)三个互不相等的数成等差数列,如果适当排列三个数,又可成为等比数列,这三个数的和为6,则这三个数为_____________.
[分析] (1)四个数成等比数列,可用第一个数与公比q表示各数,然后按所给条件列方程组求解.
(2)三个数适当排列,不同的排列方法有6种,但这里不必分成6种,因为若以三个数中哪一个数为等比中项分类,则只有三种情况,因此对于分类讨论问题,恰当的分类是解决问题的关键.3,6,12,24 -4,2,8 (2)由已知,可设这三个数为a-d,a,a+d,则a-d+a+a+d=6,∴a=2,
这三个数可表示为2-d,2,2+d,
①若2-d为等比中项,则有(2-d)2=2(2+d),解之得d=6,或d=0(舍去).此时三个数为-4,2,8.
②若2+d是等比中项,则有(2+d)2=2(2-d),解之得d=-6,或d=0(舍去).此时三个数为8,2,-4.
③若2为等比中项,则22=(2+d)·(2-d),∴d=0(舍去).
综上可知此三数为-4,2,8.例题 3忽视等比数列中奇数项符号相同、偶数项符号相同而致错 例题 4方程思想在等比数列中的应用 1.已知{an},{bn}都是等比数列,那么 ( )
A.{an+bn},{an·bn}都一定是等比数列
B.{an+bn}一定是等比数列,但{an·bn}不一定是等比数列
C.{an+bn}不一定是等比数列,但{an·bn}一定是等比数列
D.{an+bn},{an·bn}都不一定是等比数列
[解析] 当两个数列都是等比数列时,这两个数列的和不一定是等比数列,比如取两个数列是互为相反数的数列,两者的和就不是等比数列.两个等比数列的积一定是等比数列.C B 3.(2018-2019学年度山东荣成六中高二月考)已知等比数列{an}中,a2+a5=18,a3·a4=32,若an=128,q>1,则n= ( )
A.8 B.7
C.6 D.5A 4.已知等比数列{an}中,a4=7,a6=21,则a12=_______.567 5.已知三个数成等比数列,它们的积为27,它们的平方和为91,求这三个数.
