2018_2019学年高中数学第二章数列2.5等比数列的前n项和第2课时数列求和课件新人教A版必修5(41张PPT)
文档属性
| 名称 | 2018_2019学年高中数学第二章数列2.5等比数列的前n项和第2课时数列求和课件新人教A版必修5(41张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-26 20:52:25 | ||
图片预览











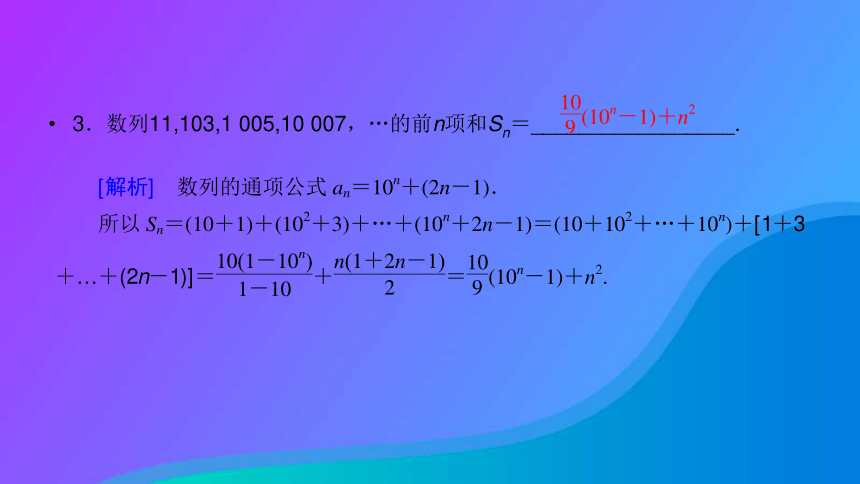
文档简介
课件41张PPT。第 二 章数列2.5 等比数列的前n项和第2课时 数列求和自主预习学案中世纪,意大利数学家斐波那契(1170~1250)在1202年发表《算盘全书》一书,书中有这样一题:“今有7老妇人共往罗马,每人有7骡,每骡负7袋,每袋盛有7个面包,每个面包有7把小刀随之,问列举之物全数共几何?”
1.回顾学过数列知识填空:
(1)首项为a1,公差为d的等差数列{an}前n项和Sn=__________=________________,推导方法为______________.
(2)首项为a1,公比为q(q≠1)的等比数列{an}前n项和Sn=_______=_______.推导方法为______________.倒序相加法 错位相减法 1.设等比数列{an}的前n项和为Sn,若S10?S5=1?2,则S15?S5= ( )
A.3?4 B.2?3
C.1?2 D.1?3A C
3.数列11,103,1 005,10 007,…的前n项和Sn=_________________.
4.若an=(-1)n-1·n,数列{an}的前n项和为Sn,则S50+S101=______.
[解析] ∵S50=(1-2)+(3-4)+(5-6)+…+(49-50)=-25.
S101=1+(3-2)+(5-4)+(7-6)+…+(101-100)=51,
∴S50+S101=-25+51=26.26 互动探究学案命题方向1 ?分组转化求和 已知数列1,1+2,1+2+22,…,1+2+22+…+2n,….
(1)求其通项公式an;
(2)求这个数列的前n项和Sn.
[分析] 注意观察数列的每一项可以发现,数列的第1,2,…n项依次为等比数列{an}的前n项和,其中an=2n-1.求该数列各项的和可先求通项an,再依an的特征选择求和方法.例题 1『规律总结』 分组转化求和法
如果一个数列的每一项是由几个独立的项组合而成,并且各独立项也可组成等差或等比数列,则该数列的前n项和可考虑拆项后利用公式求解.命题方向2 ?裂项相消求和例题 2
命题方向3 ?错位相减法求和例题 3『规律总结』 错位相减法
若数列{an}为等差数列,数列{bn}是等比数列,由这两个数列的对应项乘积组成的新数列为{anbn},当求该数列的前n项的和时,常常采用将{anbn}的各项乘以公比q,然后错位一项与{anbn}的同次项对应相减,即可转化为特殊数列的求和,所以这种数列求和的方法称为错位相减法.[解析] (1)由条件知an-an+1+2=0,
∴an+1-an=2.
∴数列{an}是以1为首项,以2为公差的等差数列.
∴an=1+2(n-1)=2n-1. 求数列1,a,a2,…的前n项和Sn.例题 4对于通项中含字母的数列求和,忽略对字母进行分类讨论而致误 [辨析] 错误的原因在于忽略了对a的取值进行分类讨论. 已知等差数列{an}前三项的和为-3,前三项的积为8.
(1)求等差数列{an}的通项公式;
(2)若a2,a3,a1成等比数列,求数列{|an|}的前n项和.例题 5分类讨论思想在数列求和中的应用 A C 3.(2018-2019学年度山东菏泽一中高二月考)已知数列{an}的前n项和为Sn,若Sn=1+2an,且a1=2,则S20= ( )
A.219-1 B.221-2
C.219+1 D.221+2B 4.已知等比数列{an}的前n项和Sn=2n-1,则a+a+…+a等于____________.
1.回顾学过数列知识填空:
(1)首项为a1,公差为d的等差数列{an}前n项和Sn=__________=________________,推导方法为______________.
(2)首项为a1,公比为q(q≠1)的等比数列{an}前n项和Sn=_______=_______.推导方法为______________.倒序相加法 错位相减法 1.设等比数列{an}的前n项和为Sn,若S10?S5=1?2,则S15?S5= ( )
A.3?4 B.2?3
C.1?2 D.1?3A C
3.数列11,103,1 005,10 007,…的前n项和Sn=_________________.
4.若an=(-1)n-1·n,数列{an}的前n项和为Sn,则S50+S101=______.
[解析] ∵S50=(1-2)+(3-4)+(5-6)+…+(49-50)=-25.
S101=1+(3-2)+(5-4)+(7-6)+…+(101-100)=51,
∴S50+S101=-25+51=26.26 互动探究学案命题方向1 ?分组转化求和 已知数列1,1+2,1+2+22,…,1+2+22+…+2n,….
(1)求其通项公式an;
(2)求这个数列的前n项和Sn.
[分析] 注意观察数列的每一项可以发现,数列的第1,2,…n项依次为等比数列{an}的前n项和,其中an=2n-1.求该数列各项的和可先求通项an,再依an的特征选择求和方法.例题 1『规律总结』 分组转化求和法
如果一个数列的每一项是由几个独立的项组合而成,并且各独立项也可组成等差或等比数列,则该数列的前n项和可考虑拆项后利用公式求解.命题方向2 ?裂项相消求和例题 2
命题方向3 ?错位相减法求和例题 3『规律总结』 错位相减法
若数列{an}为等差数列,数列{bn}是等比数列,由这两个数列的对应项乘积组成的新数列为{anbn},当求该数列的前n项的和时,常常采用将{anbn}的各项乘以公比q,然后错位一项与{anbn}的同次项对应相减,即可转化为特殊数列的求和,所以这种数列求和的方法称为错位相减法.[解析] (1)由条件知an-an+1+2=0,
∴an+1-an=2.
∴数列{an}是以1为首项,以2为公差的等差数列.
∴an=1+2(n-1)=2n-1. 求数列1,a,a2,…的前n项和Sn.例题 4对于通项中含字母的数列求和,忽略对字母进行分类讨论而致误 [辨析] 错误的原因在于忽略了对a的取值进行分类讨论. 已知等差数列{an}前三项的和为-3,前三项的积为8.
(1)求等差数列{an}的通项公式;
(2)若a2,a3,a1成等比数列,求数列{|an|}的前n项和.例题 5分类讨论思想在数列求和中的应用 A C 3.(2018-2019学年度山东菏泽一中高二月考)已知数列{an}的前n项和为Sn,若Sn=1+2an,且a1=2,则S20= ( )
A.219-1 B.221-2
C.219+1 D.221+2B 4.已知等比数列{an}的前n项和Sn=2n-1,则a+a+…+a等于____________.
