7.1.1平面直角坐标系-有序数对 课件(共22张PPT)
文档属性
| 名称 | 7.1.1平面直角坐标系-有序数对 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-27 00:00:00 | ||
图片预览








文档简介
课件22张PPT。请跟我一起走进数学的这里埋藏着丰富的乐园宝藏殿堂这是一个数字的 天安门广场上出现了壮观的背景图案,你知道它是怎么组成的吗? 参加图案表演的每个人都根据图案设计要求,按排号、列号站在一个确定的位置.随着信号举起不同颜色的花束,整个方阵就组成了绚丽的背景图案.类似于用“第几排第几列”来确定同学的位置,在数学中通常建立平面直角坐标系,用具有特定含义的两个数来刻画点的位置.本章学习平面直角坐标系这一重要工具后,同学们会发现,运用数学解决问题的能力又有提高了.比如,同学们学习有序数对后,就会设计一些简单漂亮的图案了. 7.1.1有序数对
第七章 平面直角坐标系学校:乌鲁木齐市第97中学
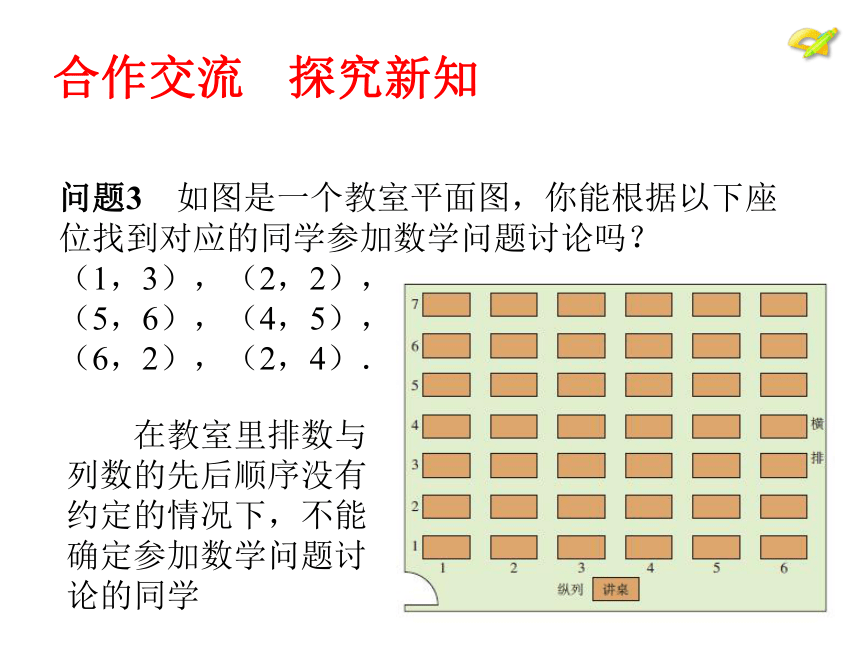
问题1 同学们都有去影剧院看电影的经历,你怎么找到自己的座位? 根据入场券上的“排数”和“号数”便可以准确地“对号入座”.问题2 你若发现一本书某页有一处印刷错误,怎样告诉其他同学这一处的位置? 说明该页上“第几行”和“第几个字”,同学就可以快速找到错误的位置了.独立思考问题3 如图是一个教室平面图,你能根据以下座位找到对应的同学参加数学问题讨论吗?
(1,3),(2,2),
(5,6),(4,5),
(6,2),(2,4).合作交流 探究新知 在教室里排数与列数的先后顺序没有约定的情况下,不能确定参加数学问题讨论的同学合作交流 探究新知追问1 假设在问题4中约定“列数在前,排数在后”,你能在图中标出参加数学问题讨论的同学的座位吗?问题3 如图是一个教室平面图,你能根据以下座位找到对应的
同学参加数学问题讨论吗?
(1,3),(2,2),(5,6),(4,5),(6,2),(2,4).追问2 由上面可知,“第1列第3排”简记为(1,3)(约定列在前,排在后),那么“第3列第5排”能简记成什么?(6,7)表示的含义是什么?追问3 同样约定“列数在前,排数在后”。(2,4)和(4,2)在同一个位置吗?追问4 假设在问题4中约定“排数在前,列数在后”,你能在图中标出参加数学问题讨论的同学的座位吗?追问5 你认为需要几个数据能确定一个位置? 有顺序的两个数 a与 b 组成的数对叫做有序数对。 记作( a,b )有序数对:认识新定义有序数对两个数字,有顺序两边用括号,中间用逗号姓名特征写法(1)数对中的两个数所表示的含义是有顺序的,数对中的两个数字是有序的.
(2)若将(a,b) 两数颠倒位置(b,a), 则点也会改变位置.注 意规则:
老师随机指定同学,这位同学要马上站起来并大声说出自己的位置。我们约定“列数在前,排数在后”。如XXX:“我叫XXX,我在第几列第几排。” 你能举出一些用有序数对来表示位置的例子吗? 3排8号3排6号3排4号4排4号4排8号5排8号5排6号6排
3号 在地球上有横线和竖线,连接两极点的竖线叫经线,垂直于经线的横线圈为纬线。根据经纬线可以确定地球上任何一点的正确位置,如北京在北纬40°,东经116° 1. 这是某同学写出来的几个有序数对,哪些写对了?A (5、9)B (x,y)E (b,9)C 4,6D (a b)×××√慧眼识英雄学以致用√2、下列语句中不能确定具体位置的是( )
A 11排7号 B 北偏东30o
C 复兴路105号 D 东经118o,北纬40oBD4.填空
如果用(7,3)表示七年级三班,则(3,7)可以表示是_____________.
三年级七班5、根据下列条件,说出能确定位置的有哪几个?
(1)座位是2排4号
(2)确山二中在东经114023ˊ37〞北纬32010ˊ7〞
(3)甲地距我市29km
√√如右图,方块中有25个汉字,用C3表示“天”那么按下列要求排列会组成一句什么话,把它读出来。读一读(1)A5 A3 C4 E5 B1 C2 B4
(2)B4 C2 D4 C5 A1 D3 E1可 爱 的 女 孩 是 我我 是 一 个 小 帅 哥A B C D E 1 2 3 4 5(1)(1,5)(1,3)(3,4)(5,5)(2,1)(3,2)(2,4)
(2)(2,4)(3,2)(4,4)(3,5)(1,1)(4,3)(5,1) 1.表格中的汉字,按顺序读出来,恰好是唐代诗人李白的《静夜思》中的两句诗,表中“句”的位置记作( 2, 1 ),请用有序数对表示出正确的读法,并写出来。拓展延伸 如图是一台雷达探测相关目标得到的结果,如果记图中目标A的位置为(2,90°),你能帮侦察员把其余各目标的位置上报给总部?B(5, 30°)C(4,240°)D(3,300°)E(6,120°)挑战自我1.有序数对的概念,表示方法说说你的收获2.平面内某个点的位置可用有序数对 来表示;3.通过本课的学习,体会数学来源于
生活,又应用于生活。有序数对谢谢大家再 见再 见再 见再 见再 见
第七章 平面直角坐标系学校:乌鲁木齐市第97中学
问题1 同学们都有去影剧院看电影的经历,你怎么找到自己的座位? 根据入场券上的“排数”和“号数”便可以准确地“对号入座”.问题2 你若发现一本书某页有一处印刷错误,怎样告诉其他同学这一处的位置? 说明该页上“第几行”和“第几个字”,同学就可以快速找到错误的位置了.独立思考问题3 如图是一个教室平面图,你能根据以下座位找到对应的同学参加数学问题讨论吗?
(1,3),(2,2),
(5,6),(4,5),
(6,2),(2,4).合作交流 探究新知 在教室里排数与列数的先后顺序没有约定的情况下,不能确定参加数学问题讨论的同学合作交流 探究新知追问1 假设在问题4中约定“列数在前,排数在后”,你能在图中标出参加数学问题讨论的同学的座位吗?问题3 如图是一个教室平面图,你能根据以下座位找到对应的
同学参加数学问题讨论吗?
(1,3),(2,2),(5,6),(4,5),(6,2),(2,4).追问2 由上面可知,“第1列第3排”简记为(1,3)(约定列在前,排在后),那么“第3列第5排”能简记成什么?(6,7)表示的含义是什么?追问3 同样约定“列数在前,排数在后”。(2,4)和(4,2)在同一个位置吗?追问4 假设在问题4中约定“排数在前,列数在后”,你能在图中标出参加数学问题讨论的同学的座位吗?追问5 你认为需要几个数据能确定一个位置? 有顺序的两个数 a与 b 组成的数对叫做有序数对。 记作( a,b )有序数对:认识新定义有序数对两个数字,有顺序两边用括号,中间用逗号姓名特征写法(1)数对中的两个数所表示的含义是有顺序的,数对中的两个数字是有序的.
(2)若将(a,b) 两数颠倒位置(b,a), 则点也会改变位置.注 意规则:
老师随机指定同学,这位同学要马上站起来并大声说出自己的位置。我们约定“列数在前,排数在后”。如XXX:“我叫XXX,我在第几列第几排。” 你能举出一些用有序数对来表示位置的例子吗? 3排8号3排6号3排4号4排4号4排8号5排8号5排6号6排
3号 在地球上有横线和竖线,连接两极点的竖线叫经线,垂直于经线的横线圈为纬线。根据经纬线可以确定地球上任何一点的正确位置,如北京在北纬40°,东经116° 1. 这是某同学写出来的几个有序数对,哪些写对了?A (5、9)B (x,y)E (b,9)C 4,6D (a b)×××√慧眼识英雄学以致用√2、下列语句中不能确定具体位置的是( )
A 11排7号 B 北偏东30o
C 复兴路105号 D 东经118o,北纬40oBD4.填空
如果用(7,3)表示七年级三班,则(3,7)可以表示是_____________.
三年级七班5、根据下列条件,说出能确定位置的有哪几个?
(1)座位是2排4号
(2)确山二中在东经114023ˊ37〞北纬32010ˊ7〞
(3)甲地距我市29km
√√如右图,方块中有25个汉字,用C3表示“天”那么按下列要求排列会组成一句什么话,把它读出来。读一读(1)A5 A3 C4 E5 B1 C2 B4
(2)B4 C2 D4 C5 A1 D3 E1可 爱 的 女 孩 是 我我 是 一 个 小 帅 哥A B C D E 1 2 3 4 5(1)(1,5)(1,3)(3,4)(5,5)(2,1)(3,2)(2,4)
(2)(2,4)(3,2)(4,4)(3,5)(1,1)(4,3)(5,1) 1.表格中的汉字,按顺序读出来,恰好是唐代诗人李白的《静夜思》中的两句诗,表中“句”的位置记作( 2, 1 ),请用有序数对表示出正确的读法,并写出来。拓展延伸 如图是一台雷达探测相关目标得到的结果,如果记图中目标A的位置为(2,90°),你能帮侦察员把其余各目标的位置上报给总部?B(5, 30°)C(4,240°)D(3,300°)E(6,120°)挑战自我1.有序数对的概念,表示方法说说你的收获2.平面内某个点的位置可用有序数对 来表示;3.通过本课的学习,体会数学来源于
生活,又应用于生活。有序数对谢谢大家再 见再 见再 见再 见再 见
