2018_2019学年高中数学第三章不等式3.2一元二次不等式及其解法第1课时一元二次不等式及其解法课件新人教A版必修5(36张PPT)
文档属性
| 名称 | 2018_2019学年高中数学第三章不等式3.2一元二次不等式及其解法第1课时一元二次不等式及其解法课件新人教A版必修5(36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-27 08:29:42 | ||
图片预览











文档简介
课件36张PPT。第 三 章不等式3.2 一元二次不等式及其解法第1课时 一元二次不等式及其解法自主预习学案在2010年温哥华冬奥会跳台滑雪比赛中,一位跳台滑雪运动员在90 m级跳台滑雪时,想使自己的飞行距离超过68 m.他若以自身体重从起滑台起滑,经助滑道于台端飞起时的初速度最快为110 km/h.
那么他能实现自己的目标吗?1.一元二次不等式的概念及形式
(1)概念:我们把只含有________未知数,并且知数的最高次数是_____的不等式,称为一元二次不等式.
(2)形式:
①ax2+bx+c>0(a≠0);
②ax2+bx+c≥0(a≠0);
③ax2+bx+c<0(a≠0);
④ax2+bx+c≤0(a≠0).一个 2 2.一元二次不等式的解集的概念及三个“二次”之间的关系
(1)一元二次不等式的解集的概念:
一般地,使某个一元二次不等式________的x的______叫做这个不等式的解,一元二次不等式的__________组成的集合叫做这个一元二次不等式的________.
(2)关于x的一元二次不等式ax2+bx+c>0(a≠0)或ax2+bx+c<0(a≠0)的解集;
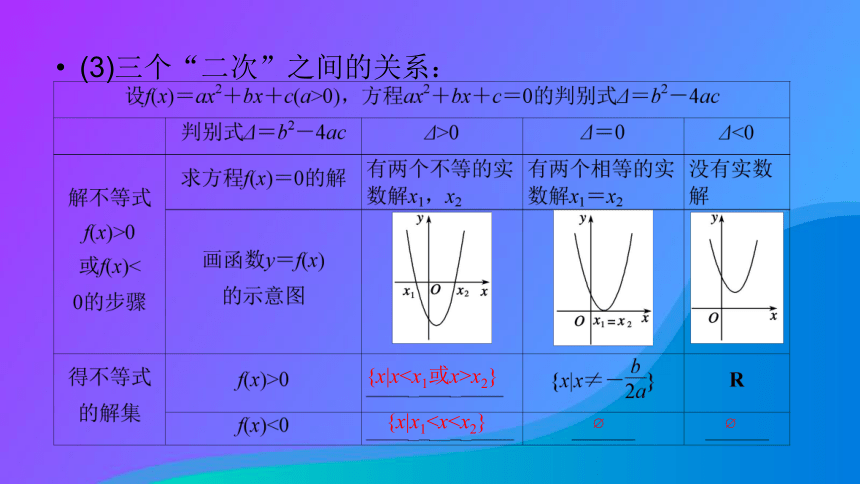
若二次函数为f(x)=ax2+bx+c(a≠0),则一元二次不等式f(x)>0或f(x)<0的解集,就是分别使二次函数f(x)的__________为正值或负值时___________的取值的集合.成立 值 所有解 解集 函数值 自变量x (3)三个“二次”之间的关系:{x|xx2} {x|x13.不等式-x2-5x+6≤0的解集为 ( )
A.{x|x≥6或x≤-1} B.{x|x≤2或x≥3}
C.{x|-6≤x≤1} D.{x|x≤-6或x≥1}
[解析] 不等式-x2-5x+6≤0可化为x2+5x-6≥0,
∴(x+6)(x-1)≥0,
∴x≤-6或x≥1,故选D.
D
4.画出函数y=x2-2x-3的图象,根据图象填空.
(1)x∈______________时,y=0,方程x2-2x-3=0的根为________________;
(2)x∈______________________时,y>0,∴不等式x2-2x-3>0的解集为______________________;
(3)x∈___________________时,y<0,∴不等式x2-2x-3<0的解集为___________________.{-1,3} x1=-1,x2=3 {x|x<-1或x>3} {x|x<-1或x>3} {x|-1由图象可知,当x∈{-1,3}时,y=0,方程x2-2x-3=0的根为x1=-1,x2=3.
当x∈{x|x<-1或x>3}时,y>0,
∴不等式x2-2x-3>0的解集为{x|x<-1或x>3}.
当x∈{x|-1(1)2x2-3x-2>0;
(2)-3x2+6x>2.互动探究学案命题方向1 ?一元二次不等式的解法 解下列不等式:
(1)x2-3x+5>0; (2)-6x2-x+2≥0;
(3)-4x2≥1-4x; (4)2x2-4x+7<0.
[解析] (1)∵Δ=(-3)2-4×5=9-20<0,
∴x2-3x+5>0的解集为R.例题 1『规律总结』 解一元二次不等式的一般步骤:
第一步,将一元二次不等式化为一端为0的形式(习惯上二次项系数大于0).
第二步,求出相应一元二次方程的根,或判断出方程没有实根.
第三步,画出相应二次函数示意草图,方程有根的将根标在图中.
第四步,观察图象中位于x轴上方或下方的部分,对比不等式中不等号的方向,写出解集.〔跟踪练习1〕
解下列不等式:
(1)3x2+5x-2≤0;
(2)x2-4x+5>0.命题方向2 ?“三个二次”关系的应用例题 2『规律总结』 1.一元二次不等式ax2+bx+c>0(a≠0)的解集的端点值是一元二次方程ax2+bx+c=0的根,也是函数y=ax2+bx+c的图象与x轴交点的横坐标.
2.注意灵活运用根与系数的关系解决问题. 解关于x的不等式-x2+5x-4>0.
[错解] ∵方程-x2+5x-4=0的两根分别为x1=1,x2=4,∴原不等式的解集为{x|x<1或x>4}.
[辨析] 由于二次项系数为负数,所以在求解时需将二次项系数转化为正数,化为正数可以同乘-1,也可以移项,具体解题时,一定要注意不等号的方向.
[正解] 原不等式等价于x2-5x+4<0,∵方程x2-5x+4=0的两根分别为x1=1,x2=4,
∴原不等式的解集为{x|10},则S∩T= ( )
A.[2,3]
B.(-∞,2]∪[3,+∞)
C.[3,+∞)
D.(0,2]∪[3,+∞)
[解析] 集合S=(-∞,2]∪[3,+∞),结合数轴,可得S∩T=(0,2]∪[3,+∞).D
3.若9-x2≤0,则 ( )
A.0≤x≤3 B.-3≤x≤0
C.-3≤x≤3 D.x≤-3或x≥3
[解析] 9-x2≤0?x2≥9?x≥3或x≤-3,故选D.D
4.二次函数y=ax2+bx+c(x∈R)的部分对应值如下表:
则不等式ax2+bx+c>0的解集为______________________.
[解析] 由表可知方程ax2+bx+c=0的两根分别为-2,3且开口向上,
∴ax2+bx+c>0的解集为{x|x<-2或x>3}.{x|x<-2或x>3}
那么他能实现自己的目标吗?1.一元二次不等式的概念及形式
(1)概念:我们把只含有________未知数,并且知数的最高次数是_____的不等式,称为一元二次不等式.
(2)形式:
①ax2+bx+c>0(a≠0);
②ax2+bx+c≥0(a≠0);
③ax2+bx+c<0(a≠0);
④ax2+bx+c≤0(a≠0).一个 2 2.一元二次不等式的解集的概念及三个“二次”之间的关系
(1)一元二次不等式的解集的概念:
一般地,使某个一元二次不等式________的x的______叫做这个不等式的解,一元二次不等式的__________组成的集合叫做这个一元二次不等式的________.
(2)关于x的一元二次不等式ax2+bx+c>0(a≠0)或ax2+bx+c<0(a≠0)的解集;
若二次函数为f(x)=ax2+bx+c(a≠0),则一元二次不等式f(x)>0或f(x)<0的解集,就是分别使二次函数f(x)的__________为正值或负值时___________的取值的集合.成立 值 所有解 解集 函数值 自变量x (3)三个“二次”之间的关系:{x|x
A.{x|x≥6或x≤-1} B.{x|x≤2或x≥3}
C.{x|-6≤x≤1} D.{x|x≤-6或x≥1}
[解析] 不等式-x2-5x+6≤0可化为x2+5x-6≥0,
∴(x+6)(x-1)≥0,
∴x≤-6或x≥1,故选D.
D
4.画出函数y=x2-2x-3的图象,根据图象填空.
(1)x∈______________时,y=0,方程x2-2x-3=0的根为________________;
(2)x∈______________________时,y>0,∴不等式x2-2x-3>0的解集为______________________;
(3)x∈___________________时,y<0,∴不等式x2-2x-3<0的解集为___________________.{-1,3} x1=-1,x2=3 {x|x<-1或x>3} {x|x<-1或x>3} {x|-1
当x∈{x|x<-1或x>3}时,y>0,
∴不等式x2-2x-3>0的解集为{x|x<-1或x>3}.
当x∈{x|-1
(2)-3x2+6x>2.互动探究学案命题方向1 ?一元二次不等式的解法 解下列不等式:
(1)x2-3x+5>0; (2)-6x2-x+2≥0;
(3)-4x2≥1-4x; (4)2x2-4x+7<0.
[解析] (1)∵Δ=(-3)2-4×5=9-20<0,
∴x2-3x+5>0的解集为R.例题 1『规律总结』 解一元二次不等式的一般步骤:
第一步,将一元二次不等式化为一端为0的形式(习惯上二次项系数大于0).
第二步,求出相应一元二次方程的根,或判断出方程没有实根.
第三步,画出相应二次函数示意草图,方程有根的将根标在图中.
第四步,观察图象中位于x轴上方或下方的部分,对比不等式中不等号的方向,写出解集.〔跟踪练习1〕
解下列不等式:
(1)3x2+5x-2≤0;
(2)x2-4x+5>0.命题方向2 ?“三个二次”关系的应用例题 2『规律总结』 1.一元二次不等式ax2+bx+c>0(a≠0)的解集的端点值是一元二次方程ax2+bx+c=0的根,也是函数y=ax2+bx+c的图象与x轴交点的横坐标.
2.注意灵活运用根与系数的关系解决问题. 解关于x的不等式-x2+5x-4>0.
[错解] ∵方程-x2+5x-4=0的两根分别为x1=1,x2=4,∴原不等式的解集为{x|x<1或x>4}.
[辨析] 由于二次项系数为负数,所以在求解时需将二次项系数转化为正数,化为正数可以同乘-1,也可以移项,具体解题时,一定要注意不等号的方向.
[正解] 原不等式等价于x2-5x+4<0,∵方程x2-5x+4=0的两根分别为x1=1,x2=4,
∴原不等式的解集为{x|1
A.[2,3]
B.(-∞,2]∪[3,+∞)
C.[3,+∞)
D.(0,2]∪[3,+∞)
[解析] 集合S=(-∞,2]∪[3,+∞),结合数轴,可得S∩T=(0,2]∪[3,+∞).D
3.若9-x2≤0,则 ( )
A.0≤x≤3 B.-3≤x≤0
C.-3≤x≤3 D.x≤-3或x≥3
[解析] 9-x2≤0?x2≥9?x≥3或x≤-3,故选D.D
4.二次函数y=ax2+bx+c(x∈R)的部分对应值如下表:
则不等式ax2+bx+c>0的解集为______________________.
[解析] 由表可知方程ax2+bx+c=0的两根分别为-2,3且开口向上,
∴ax2+bx+c>0的解集为{x|x<-2或x>3}.{x|x<-2或x>3}
