2018_2019学年高中数学第三章不等式3.3二元一次不等式(组)与简单的线性规划问题第2课时线性规划的概念课件新人教A版必修5(43张PPT)
文档属性
| 名称 | 2018_2019学年高中数学第三章不等式3.3二元一次不等式(组)与简单的线性规划问题第2课时线性规划的概念课件新人教A版必修5(43张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-27 08:32:32 | ||
图片预览










文档简介
课件43张PPT。第 三 章不等式3.3 二元一次不等式(组)与简单的线性规划问题第2课时 线性规划的概念自主预习学案战国时期的齐国大臣田忌与国王赛马,用自己的下等马对国王的上等马,用自己的上等马对国王的中等马,用自己的中等马对国王的下等马,这样田忌以2∶1取得了胜利,这个故事讲述了规划的威力.实际生产生活中,我们常常希望以最少的投入获得最大的回报.线性规划提供了解决优化问题的有效工具.线性规划中的基本概念二元一次 一次函数 解 集合 可行解 D [解析] 根据题意作出可行域,如图阴影部分所示,由z=x+y得y=-x+z.
作出直线y=-x,并平移该直线,
当直线y=-x+z过点A时,目标函数取最大值.
由图知A(3,0),
故zmax=3+0=3.
故选D.A A 3 [解析] 不等式组表示的平面区域如图所示.
作直线l0:2x+y=0,平移直线l0,当直线l0经过平面区域内的点A(2,-1)时,z取最大值2×2-1=3.互动探究学案命题方向1 ?求线性目标函数的最值问题例题 1[分析] 由于所给约束条件及目标函数均为关于x、y的一次式,所以此问题是简单线性规划问题,使用图解法求解.
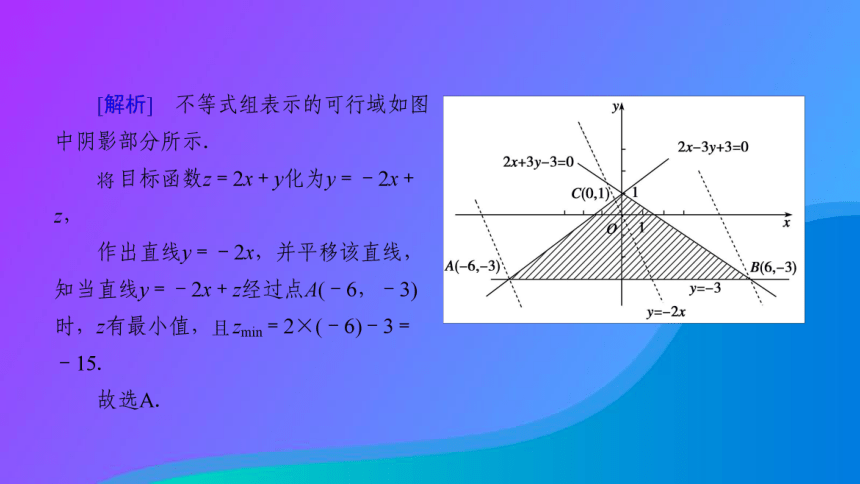
[解析] 作出不等式组表示的平面区域(即可行域),如图所示.
把z=2x+y变形为y=-2x+z,得到斜率为-2,在y轴上的截距为z,随z变化的一族平行直线.
由图可看出,当直线z=2x+y经过可行域上的点A时,截距z最大,经过点B时,截距z最小.『规律总结』 (1)解线性规划问题的关键是准确地作出可行域,正确理解z的几何意义,对一个封闭图形而言,最优解一般在可行域的边界线交点处或边界线上取得.在解题中也可由此快速找到最大值点或最小值点.
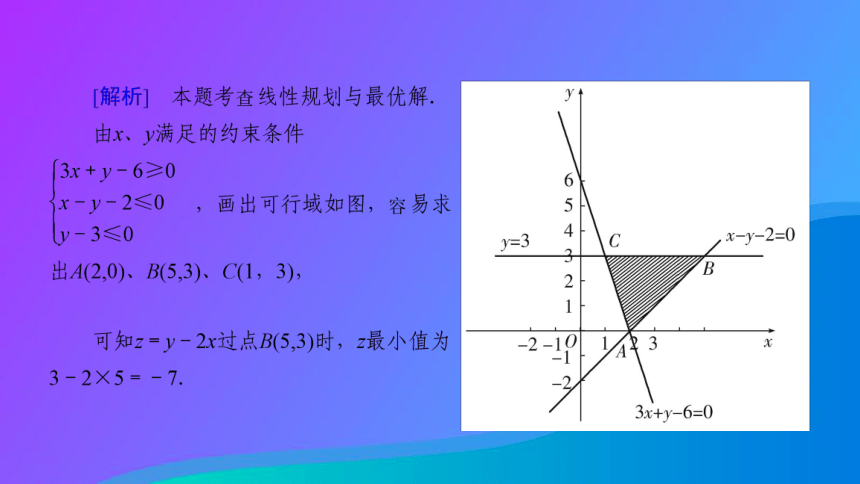
(2)要注意直线斜率的大小.D 命题方向2 ?简单的线性规划中的整数解[分析] 先作出不等式组所表示的可行域,需要注意的是这里的x、y是整数,故只是可行域内的整数点,然后作出与直线7x+5y=0平行的直线再进行观察.例题 2『规律总结』 在求解最优解为整数点的题型时,若最优解不在直线的交点处,应考虑可行域中距离邻近最优解的边界线附近的整点,比较后作出正确的解答.D 命题方向3 ?非线性目标函数的最值问题例题 3『规律总结』 求非线性目标函数的最值,要注意分析充分利用目标函数所表示的几何意义,通常与截距、斜率、距离等联系.C D 例题 4[错解] 由题意,作出可行域如图所示.[辨析] 作图不准确.目标函数变形后对应的直线画的方向不准确,导致求最优解时,对应点的位置找错.[警示] 在求目标函数的最优解时,必须准确地作出可行域以及目标函数对应的直线,最为关键的是弄清楚这些直线斜率之间的关系.例题 5已知目标函数的最值求参数 D B D [解析] 画出可行域,如图中阴影所示.
又目标函数z=x+y,
结合图象易知y=-x+z过(0,3)点时z取得最大值,
即zmax=0+3=3.
故选D.A [5,7)
作出直线y=-x,并平移该直线,
当直线y=-x+z过点A时,目标函数取最大值.
由图知A(3,0),
故zmax=3+0=3.
故选D.A A 3 [解析] 不等式组表示的平面区域如图所示.
作直线l0:2x+y=0,平移直线l0,当直线l0经过平面区域内的点A(2,-1)时,z取最大值2×2-1=3.互动探究学案命题方向1 ?求线性目标函数的最值问题例题 1[分析] 由于所给约束条件及目标函数均为关于x、y的一次式,所以此问题是简单线性规划问题,使用图解法求解.
[解析] 作出不等式组表示的平面区域(即可行域),如图所示.
把z=2x+y变形为y=-2x+z,得到斜率为-2,在y轴上的截距为z,随z变化的一族平行直线.
由图可看出,当直线z=2x+y经过可行域上的点A时,截距z最大,经过点B时,截距z最小.『规律总结』 (1)解线性规划问题的关键是准确地作出可行域,正确理解z的几何意义,对一个封闭图形而言,最优解一般在可行域的边界线交点处或边界线上取得.在解题中也可由此快速找到最大值点或最小值点.
(2)要注意直线斜率的大小.D 命题方向2 ?简单的线性规划中的整数解[分析] 先作出不等式组所表示的可行域,需要注意的是这里的x、y是整数,故只是可行域内的整数点,然后作出与直线7x+5y=0平行的直线再进行观察.例题 2『规律总结』 在求解最优解为整数点的题型时,若最优解不在直线的交点处,应考虑可行域中距离邻近最优解的边界线附近的整点,比较后作出正确的解答.D 命题方向3 ?非线性目标函数的最值问题例题 3『规律总结』 求非线性目标函数的最值,要注意分析充分利用目标函数所表示的几何意义,通常与截距、斜率、距离等联系.C D 例题 4[错解] 由题意,作出可行域如图所示.[辨析] 作图不准确.目标函数变形后对应的直线画的方向不准确,导致求最优解时,对应点的位置找错.[警示] 在求目标函数的最优解时,必须准确地作出可行域以及目标函数对应的直线,最为关键的是弄清楚这些直线斜率之间的关系.例题 5已知目标函数的最值求参数 D B D [解析] 画出可行域,如图中阴影所示.
又目标函数z=x+y,
结合图象易知y=-x+z过(0,3)点时z取得最大值,
即zmax=0+3=3.
故选D.A [5,7)
