2018_2019学年高中数学第三章不等式3.3二元一次不等式(组)与简单的线性规划问题第3课时线性规划的应用课件新人教A版必修5(55张PPT)
文档属性
| 名称 | 2018_2019学年高中数学第三章不等式3.3二元一次不等式(组)与简单的线性规划问题第3课时线性规划的应用课件新人教A版必修5(55张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-27 08:34:53 | ||
图片预览










文档简介
课件55张PPT。第 三 章不等式3.3 二元一次不等式(组)与简单的线性规划问题第3课时 线性规划的应用自主预习学案
1.线性规划常用来解决下列问题:
(1)给定一定数量的人力、物力、资金等资源,怎样安排运用这些资源,才能使完成的任务量最______,收到的效益最______.
(2)给定一项任务,怎样统筹安排,才能使完成这项任务的人力、资金、物力资源最______.常见问题有:物资________、产品________、下料等问题.
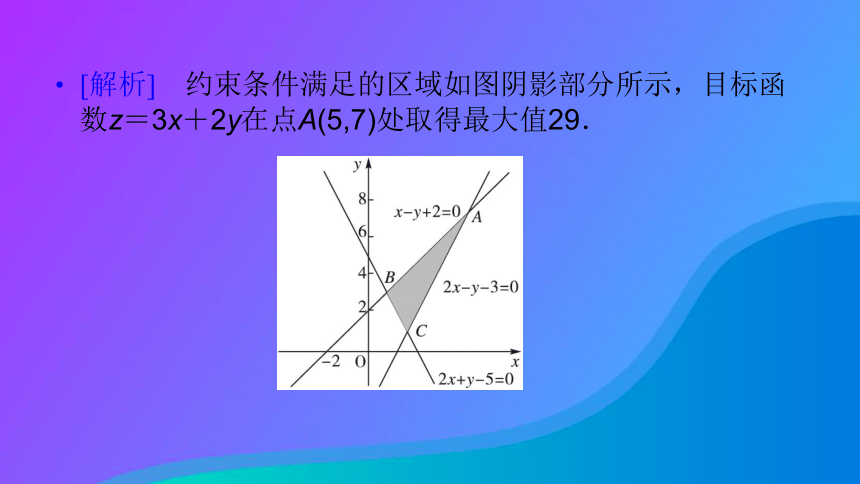
2.最优解常转化为由目标函数得到的直线到________距离的最值来考虑.(到原点距离最大(小),一般等价于纵截距最大(小))大 大 小 调运 安排 原点 D [解析] 约束条件满足的区域如图阴影部分所示,目标函数z=3x+2y在点A(5,7)处取得最大值29.
2.(2016·全国卷Ⅰ文,16)某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为____________元.216 000
目标函数为z=2100x+900y.
其可行域为四边形OMNC及其内部区域中的整点,其中点O(0,0),M(0,200),N(60,100),C(90,0),当直线z=2 100x+900y经过点N(60,100)时,z取得最大值,zmax=2100×60+900×100=216 000,即生产产品A、产品B的利润之和的最大值为216 000元.已知电视台每周安排的甲、乙连续剧的总播放时间不多于600 min,广告的总播放时间不少于30 min,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用x、y表示每周计划 ((1)用x、y列出满足题目条件的数学关系式,并画出相应的平面区域;
(2)问电视台每周播出甲、乙两套连续剧各多少次,才能使总收视人次最多?该二元一次不等式组所表示的平面区域为图①中的阴影部分中的整数点.互动探究学案命题方向1 ?收益最大问题(利润、收入、产量等) 某工厂计划生产甲、乙两种产品,这两种产品都需要两种原料.生产甲产品1工时需要A种原料3 kg,B种原料1 kg;生产乙产品1工时需要A种原料2 kg,B种原料2 kg.现有A种原料1 200 kg,B种原料800 kg.如果生产甲产品每工时的平均利润是30元,生产乙产品每工时的平均利润是40元,问甲、乙两种产品各生产多少工时能使利润的总额最大?最大利润是多少?例题 1于是问题转化为,在x、y满足条件②的情况下,求t=30x+40y的最大值.
画出不等式组②表示的平面区域OABC如图.问题又可以转化为,在不等式组②表示的平面区域内找一点,把它的坐标代入式子30x+40y时,使该式取最大值.『规律总结』 解答线性规划应用题的一般步骤:
(1)审题——仔细阅读,准确理解题意,明确有哪些限制条件,起关键作用的变量有哪些.由于线性规划应用题中的量较多,为了理顺题目中量与量之间的关系,有时可借助表格来处理.
(2)转化——设出未知量,由条件列出约束条件确立目标函数,从而将实际问题转化为线性规划问题.
(3)作图——作出可行域,求出可行域边界点的坐标.(4)求解——利用图形法求出最优解和最值.
(5)作答——就应用题提出的问题作出回答.
几个注意点:(1)列不等式组时,要特别注意表达不等关系的词语(如不超过,不大于,最少等);(2)平移直线时,特别注意斜率大小与直线的倾斜程度,准确找出最优解对应直线的位置;(3)将求解得到数学结论转化为实际问题的结论.〔跟踪练习1〕
某厂计划生产甲、乙两种产品,甲产品售价50千元/件,乙产品售价30千元/件,生产这两种产品需要A、B两种原料,生产甲产品需要A种原料4 t/件,B种原料2 t/件,生产乙产品需要A种原料3 t/件,B种原料1 t/件,该厂能获得A种原料120 t,B种原料50 t.问生产甲、乙两种产品各多少件时,能使销售总收入最大?最大总收入为多少?画出不等式组表示的平面区域即可行域如图.
易知直线z=50x+30y过点(15,20)时,取得最大值.
zmax=50×15+30×20=1 350.
答:生产甲、乙两种产品分别为15件、20件,总收入最大是1 350千元.命题方向2 ?耗费资源(人力、物力、资金等)最少问题 某公司的仓库A存有货物12 t,仓库B存有货物8 t.现按7 t、8 t和5 t把货物分别调运给甲、乙、丙三个商店,从仓库A运货物到商店甲、乙、丙,每吨货物的运费分别为8元、6元、9元、从仓库B运货物到商店甲、乙、丙,每吨货物的运费分别为3元、4元、5元.则应如何安排调运方案,才能使得从两个仓库运货物到三个商店的总运费最少?
[解析] 设仓库A运给甲、乙商店的货物分别为x t、y t.
则仓库A运给丙商店的货物为(12-x-y)t.
仓库B运给甲、乙、丙商店的货物分别为(7-x)t,(8-y)t,[5-(12-x-y)]t,例题 2作直线l:x-2y=0,把直线l平行移动,
当直线过A(0,8)时,z=x-2y+126取得最小值,
zmin=0-2×8+126=110,
即x=0,y=8时,总运费最少.
即仓库A运给甲、乙、丙商店的货物分别为0 t、8 t、4 t,仓库B运给甲、乙、丙商店的货物分别为7 t、0 t、1 t,此时可使得从两个仓库运货物到三个商店的总运费最少.
『规律总结』 求最优解时,常常要考虑直线的位置,精确作图又比较麻烦,这时可通过比较直线的斜率来判断其位置.〔跟踪练习2〕
某公司租赁甲、乙两种设备生产A、B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件与B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元.现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为__________元.
2 300 命题方向3 ?整数最优解不是边界点的问题 某人有楼房一幢,室内面积共计180 m2,拟分割成两类房间作为旅游客房.大房间每间面积为18 m2,可住游客5名,每名旅客每天住宿费40 元;小房间每间面积为15 m2,可以住游客3名,每名游客每天住宿费为50元;装修大房间每间需要1 000元,装修小房间每间需600元.如果他只能筹款8 000元用于装修,且游客能住满客房,他应隔出大房间和小房间各多少间,能获得最大收益?例题 3作出可行域,如图所示.当直线z=200x+150y经过可行域上的点M时,z最大.『规律总结』 整数最优解不是边界点时,要取可行域内距离最优解最近的点检验找出整数最优解,或者利用格点法(即过x轴与y轴上的整点作与坐标轴平行的直线,从网格交点中找位于可行域内使z取最值的点.)例题 4忽视线性目标函数的几何意义而致误 B
[辨析] 因为没有弄清目标函数z=2x-y的几何意义,由z=2x-y得y=2x-z,当z取最大值时,-z应取最小值,故当直线y=2x-z在y轴上截距最大时,符合题意,另外画图不够准确致错.
[警示] ①线性规划的求解是在图上进行的,因此做图是否准确直接影响到结论的正误;②要注意目标函数最值的几何意义;③要注意线性目标函数直线与围成可行域的直线的位置关系.数形结合的主要解题策略是:数?形?问题的解决;或:形?数?问题的解决.数与形结合的基本思路是:根据数的结构特征构造出与之相应的几何图形,并利用直观特征去解决的问题;或者将要解决的形的问题转化为数量关系去解决.本节中利用线性规划解决实际问题是典型的数形结合问题.线性规划中的数形结合思想 在平面直角坐标系中,点A、B、C的坐标分别为(0,1)、(4,2)、(2,6).如果P(x,y)是△ABC围成的区域(含边界)上的点,那么当w=xy取得最大
[解析] 点A、B、C围成的区域(含边界)如图所示:因为w=xy表示矩形OP1PP2的面积,例题 5值时,点P的坐标是___________.1.某旅行社租用A、B两种型号的客车安排900名客人旅行,A、B两种车辆的载客量分别为36人和60人,租金分别为1 600元/辆和2 400元/辆,旅行社要求租车总数不超过21辆,且B型车不多于A型车7辆.则租金最少为 ( )
A.31 200元 B.36 800元
C.36 000元 D.38 400元B 画出可行域,如图.
当目标函数z=1 600x+2 400y经过点A(5,12)时,zmin=1 600×5+2 400×12=36 800(元).故选B.2.某公司计划2017年在甲、乙两个电视台做总时间不超过300 min的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为500元/min和200元/min,已知甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.该公司要想获得最大收益,应分配在甲电视台_______min广告时间,乙电视台_______min广告时间,获得的最大收益为______万元.100 200 70 3.(2016·天津文,16)某化肥厂生产甲、乙两种混合肥料,需要A、B、C三种主要原料.生产1车皮甲种肥料和生产1车皮乙中肥料所需三种原料的吨数如下表所示:
现有A种原料200 t,B种原料360 t,C种原料300 t,在此基础上生产甲乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x、y表示计划生产甲、乙两种肥料的车皮数.
(1)用x、y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?并求出此最大利润.
1.线性规划常用来解决下列问题:
(1)给定一定数量的人力、物力、资金等资源,怎样安排运用这些资源,才能使完成的任务量最______,收到的效益最______.
(2)给定一项任务,怎样统筹安排,才能使完成这项任务的人力、资金、物力资源最______.常见问题有:物资________、产品________、下料等问题.
2.最优解常转化为由目标函数得到的直线到________距离的最值来考虑.(到原点距离最大(小),一般等价于纵截距最大(小))大 大 小 调运 安排 原点 D [解析] 约束条件满足的区域如图阴影部分所示,目标函数z=3x+2y在点A(5,7)处取得最大值29.
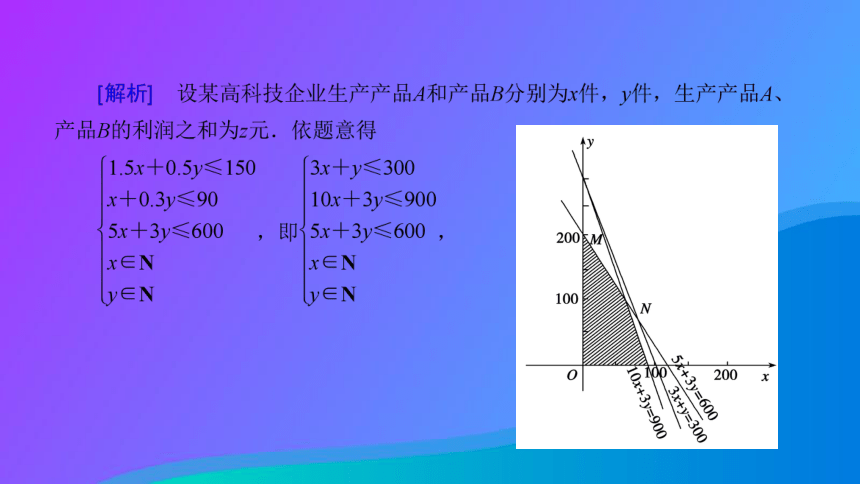
2.(2016·全国卷Ⅰ文,16)某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为____________元.216 000
目标函数为z=2100x+900y.
其可行域为四边形OMNC及其内部区域中的整点,其中点O(0,0),M(0,200),N(60,100),C(90,0),当直线z=2 100x+900y经过点N(60,100)时,z取得最大值,zmax=2100×60+900×100=216 000,即生产产品A、产品B的利润之和的最大值为216 000元.已知电视台每周安排的甲、乙连续剧的总播放时间不多于600 min,广告的总播放时间不少于30 min,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用x、y表示每周计划 ((1)用x、y列出满足题目条件的数学关系式,并画出相应的平面区域;
(2)问电视台每周播出甲、乙两套连续剧各多少次,才能使总收视人次最多?该二元一次不等式组所表示的平面区域为图①中的阴影部分中的整数点.互动探究学案命题方向1 ?收益最大问题(利润、收入、产量等) 某工厂计划生产甲、乙两种产品,这两种产品都需要两种原料.生产甲产品1工时需要A种原料3 kg,B种原料1 kg;生产乙产品1工时需要A种原料2 kg,B种原料2 kg.现有A种原料1 200 kg,B种原料800 kg.如果生产甲产品每工时的平均利润是30元,生产乙产品每工时的平均利润是40元,问甲、乙两种产品各生产多少工时能使利润的总额最大?最大利润是多少?例题 1于是问题转化为,在x、y满足条件②的情况下,求t=30x+40y的最大值.
画出不等式组②表示的平面区域OABC如图.问题又可以转化为,在不等式组②表示的平面区域内找一点,把它的坐标代入式子30x+40y时,使该式取最大值.『规律总结』 解答线性规划应用题的一般步骤:
(1)审题——仔细阅读,准确理解题意,明确有哪些限制条件,起关键作用的变量有哪些.由于线性规划应用题中的量较多,为了理顺题目中量与量之间的关系,有时可借助表格来处理.
(2)转化——设出未知量,由条件列出约束条件确立目标函数,从而将实际问题转化为线性规划问题.
(3)作图——作出可行域,求出可行域边界点的坐标.(4)求解——利用图形法求出最优解和最值.
(5)作答——就应用题提出的问题作出回答.
几个注意点:(1)列不等式组时,要特别注意表达不等关系的词语(如不超过,不大于,最少等);(2)平移直线时,特别注意斜率大小与直线的倾斜程度,准确找出最优解对应直线的位置;(3)将求解得到数学结论转化为实际问题的结论.〔跟踪练习1〕
某厂计划生产甲、乙两种产品,甲产品售价50千元/件,乙产品售价30千元/件,生产这两种产品需要A、B两种原料,生产甲产品需要A种原料4 t/件,B种原料2 t/件,生产乙产品需要A种原料3 t/件,B种原料1 t/件,该厂能获得A种原料120 t,B种原料50 t.问生产甲、乙两种产品各多少件时,能使销售总收入最大?最大总收入为多少?画出不等式组表示的平面区域即可行域如图.
易知直线z=50x+30y过点(15,20)时,取得最大值.
zmax=50×15+30×20=1 350.
答:生产甲、乙两种产品分别为15件、20件,总收入最大是1 350千元.命题方向2 ?耗费资源(人力、物力、资金等)最少问题 某公司的仓库A存有货物12 t,仓库B存有货物8 t.现按7 t、8 t和5 t把货物分别调运给甲、乙、丙三个商店,从仓库A运货物到商店甲、乙、丙,每吨货物的运费分别为8元、6元、9元、从仓库B运货物到商店甲、乙、丙,每吨货物的运费分别为3元、4元、5元.则应如何安排调运方案,才能使得从两个仓库运货物到三个商店的总运费最少?
[解析] 设仓库A运给甲、乙商店的货物分别为x t、y t.
则仓库A运给丙商店的货物为(12-x-y)t.
仓库B运给甲、乙、丙商店的货物分别为(7-x)t,(8-y)t,[5-(12-x-y)]t,例题 2作直线l:x-2y=0,把直线l平行移动,
当直线过A(0,8)时,z=x-2y+126取得最小值,
zmin=0-2×8+126=110,
即x=0,y=8时,总运费最少.
即仓库A运给甲、乙、丙商店的货物分别为0 t、8 t、4 t,仓库B运给甲、乙、丙商店的货物分别为7 t、0 t、1 t,此时可使得从两个仓库运货物到三个商店的总运费最少.
『规律总结』 求最优解时,常常要考虑直线的位置,精确作图又比较麻烦,这时可通过比较直线的斜率来判断其位置.〔跟踪练习2〕
某公司租赁甲、乙两种设备生产A、B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件与B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元.现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为__________元.
2 300 命题方向3 ?整数最优解不是边界点的问题 某人有楼房一幢,室内面积共计180 m2,拟分割成两类房间作为旅游客房.大房间每间面积为18 m2,可住游客5名,每名旅客每天住宿费40 元;小房间每间面积为15 m2,可以住游客3名,每名游客每天住宿费为50元;装修大房间每间需要1 000元,装修小房间每间需600元.如果他只能筹款8 000元用于装修,且游客能住满客房,他应隔出大房间和小房间各多少间,能获得最大收益?例题 3作出可行域,如图所示.当直线z=200x+150y经过可行域上的点M时,z最大.『规律总结』 整数最优解不是边界点时,要取可行域内距离最优解最近的点检验找出整数最优解,或者利用格点法(即过x轴与y轴上的整点作与坐标轴平行的直线,从网格交点中找位于可行域内使z取最值的点.)例题 4忽视线性目标函数的几何意义而致误 B
[辨析] 因为没有弄清目标函数z=2x-y的几何意义,由z=2x-y得y=2x-z,当z取最大值时,-z应取最小值,故当直线y=2x-z在y轴上截距最大时,符合题意,另外画图不够准确致错.
[警示] ①线性规划的求解是在图上进行的,因此做图是否准确直接影响到结论的正误;②要注意目标函数最值的几何意义;③要注意线性目标函数直线与围成可行域的直线的位置关系.数形结合的主要解题策略是:数?形?问题的解决;或:形?数?问题的解决.数与形结合的基本思路是:根据数的结构特征构造出与之相应的几何图形,并利用直观特征去解决的问题;或者将要解决的形的问题转化为数量关系去解决.本节中利用线性规划解决实际问题是典型的数形结合问题.线性规划中的数形结合思想 在平面直角坐标系中,点A、B、C的坐标分别为(0,1)、(4,2)、(2,6).如果P(x,y)是△ABC围成的区域(含边界)上的点,那么当w=xy取得最大
[解析] 点A、B、C围成的区域(含边界)如图所示:因为w=xy表示矩形OP1PP2的面积,例题 5值时,点P的坐标是___________.1.某旅行社租用A、B两种型号的客车安排900名客人旅行,A、B两种车辆的载客量分别为36人和60人,租金分别为1 600元/辆和2 400元/辆,旅行社要求租车总数不超过21辆,且B型车不多于A型车7辆.则租金最少为 ( )
A.31 200元 B.36 800元
C.36 000元 D.38 400元B 画出可行域,如图.
当目标函数z=1 600x+2 400y经过点A(5,12)时,zmin=1 600×5+2 400×12=36 800(元).故选B.2.某公司计划2017年在甲、乙两个电视台做总时间不超过300 min的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为500元/min和200元/min,已知甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.该公司要想获得最大收益,应分配在甲电视台_______min广告时间,乙电视台_______min广告时间,获得的最大收益为______万元.100 200 70 3.(2016·天津文,16)某化肥厂生产甲、乙两种混合肥料,需要A、B、C三种主要原料.生产1车皮甲种肥料和生产1车皮乙中肥料所需三种原料的吨数如下表所示:
现有A种原料200 t,B种原料360 t,C种原料300 t,在此基础上生产甲乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x、y表示计划生产甲、乙两种肥料的车皮数.
(1)用x、y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?并求出此最大利润.
