2018_2019学年高中数学第三章不等式3.4基本不等式第2课时基本不等式的应用_证明与最值问题课件新人教A版必修5(31张PPT)
文档属性
| 名称 | 2018_2019学年高中数学第三章不等式3.4基本不等式第2课时基本不等式的应用_证明与最值问题课件新人教A版必修5(31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-27 08:36:37 | ||
图片预览









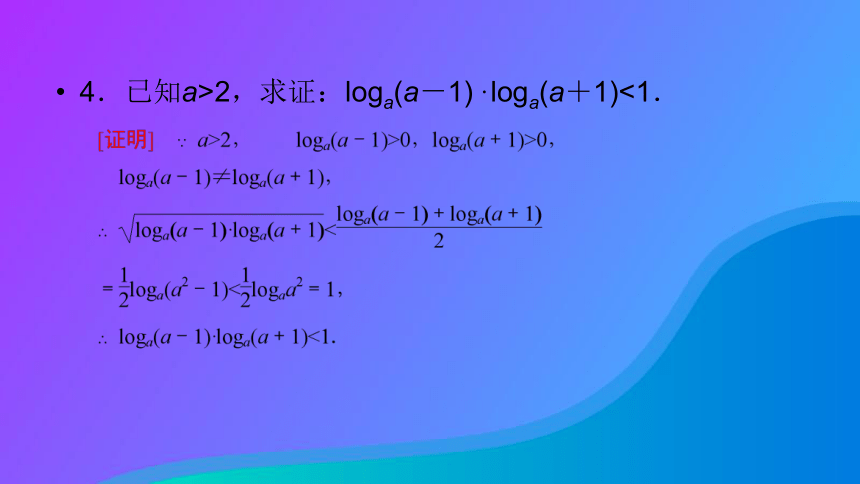

文档简介
课件31张PPT。第 三 章不等式第2课时 基本不等式的应用—证明与最值问题自主预习学案一养殖场想用栅栏围成一个长、宽分别为a、b的矩形牧场,现在已有材料能做成l km的栅栏,那么如何设计才能使围成的矩形牧场面积最大?
C B
3.已知正数a、b满足a+b=8,则+的最大值为_____.4 4.已知a>2,求证:loga(a-1)·loga(a+1)<1.互动探究学案命题方向1 ?不等式的证明技巧—字母轮换不等式的证法 求证:a4+b4+c4≥a2b2+b2c2+c2a2≥abc(a+b+c).
[分析] 本题中的表达式具有轮换对称关系,将表达式中字母轮换a→b→c→a后表达式不变,这类问题证明一般变为几个表达式(通常几个字母就需几个表达式)迭加(乘),从而获解.例题 1[证明] 先证a4+b4+c4≥a2b2+b2c2+c2a2,
∵a2+b2≥2ab(a,b∈R),
∴a4+b4≥2a2b2,b4+c4≥2b2c2,c4+a4≥2c2a2,
∴2(a4+b4+c4)≥2a2b2+2b2c2+2c2a2,
∴a4+b4+c2≥a2b2+b2c2+c2a2,
再证a2b2+b2c2+c2a2≥abc(a+b+c),
∵a2b2+b2c2=b2(a2+c2)≥2ab2c(等号在a=c时成立).
同理a2b2+a2c2≥2a2bc,(等号在b=c时成立).
b2c2+a2c2≥2abc2,(等号在a=b时成立).
三式相加得:a2b2+b2c2+c2a2≥abc(a+b+c),(等号在a=b=c时成立).『规律总结』 证明不等式时,要注意观察分析其结构特征选取相应的证明方法.若不等式中字母具有轮换对称关系,则常常连用几个形式相同字母不同的不等式迭加获证.[点评] 不能直接应用基本不等式证明的不等式和连续两次使用基本不等式等号不能同时成立的情形,要通过合理的变形,“重新组合”或者“1的代换”等技巧.构造能够运用基本不等式的条件.命题方向2 ?求参数的取值范围问题例题 2『规律总结』 1.恒成立问题求参数的取值范围,常用“分离参数”转化为函数最值问题求解;2.解题思路来源于细致的观察,丰富的联想和充分的知识、技能的储备,要注意总结记忆.例题 4忽视等号成立的条件而致误 [辨析] 误解中忽视了判定等号是否成立.例题 4均值不等式在实际问题中的应用 D A
3.已知m、n∈R,m2+n2=100,则mn的最大值是 ( )
A.100 B.50
C.20 D.10B 36
C B
3.已知正数a、b满足a+b=8,则+的最大值为_____.4 4.已知a>2,求证:loga(a-1)·loga(a+1)<1.互动探究学案命题方向1 ?不等式的证明技巧—字母轮换不等式的证法 求证:a4+b4+c4≥a2b2+b2c2+c2a2≥abc(a+b+c).
[分析] 本题中的表达式具有轮换对称关系,将表达式中字母轮换a→b→c→a后表达式不变,这类问题证明一般变为几个表达式(通常几个字母就需几个表达式)迭加(乘),从而获解.例题 1[证明] 先证a4+b4+c4≥a2b2+b2c2+c2a2,
∵a2+b2≥2ab(a,b∈R),
∴a4+b4≥2a2b2,b4+c4≥2b2c2,c4+a4≥2c2a2,
∴2(a4+b4+c4)≥2a2b2+2b2c2+2c2a2,
∴a4+b4+c2≥a2b2+b2c2+c2a2,
再证a2b2+b2c2+c2a2≥abc(a+b+c),
∵a2b2+b2c2=b2(a2+c2)≥2ab2c(等号在a=c时成立).
同理a2b2+a2c2≥2a2bc,(等号在b=c时成立).
b2c2+a2c2≥2abc2,(等号在a=b时成立).
三式相加得:a2b2+b2c2+c2a2≥abc(a+b+c),(等号在a=b=c时成立).『规律总结』 证明不等式时,要注意观察分析其结构特征选取相应的证明方法.若不等式中字母具有轮换对称关系,则常常连用几个形式相同字母不同的不等式迭加获证.[点评] 不能直接应用基本不等式证明的不等式和连续两次使用基本不等式等号不能同时成立的情形,要通过合理的变形,“重新组合”或者“1的代换”等技巧.构造能够运用基本不等式的条件.命题方向2 ?求参数的取值范围问题例题 2『规律总结』 1.恒成立问题求参数的取值范围,常用“分离参数”转化为函数最值问题求解;2.解题思路来源于细致的观察,丰富的联想和充分的知识、技能的储备,要注意总结记忆.例题 4忽视等号成立的条件而致误 [辨析] 误解中忽视了判定等号是否成立.例题 4均值不等式在实际问题中的应用 D A
3.已知m、n∈R,m2+n2=100,则mn的最大值是 ( )
A.100 B.50
C.20 D.10B 36
