2018_2019学年高中数学第一章解三角形1.2应用举例第2课时高度角度问题课件新人教A版必修5(44张PPT)
文档属性
| 名称 | 2018_2019学年高中数学第一章解三角形1.2应用举例第2课时高度角度问题课件新人教A版必修5(44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-27 08:38:59 | ||
图片预览










文档简介
课件44张PPT。第 一 章解三角形1.2 应用举例第2课时 高度、角度问题自主预习学案“遥不可及的月亮离我们地球究竟有多远呢?”在古代,天文学家没有先进的仪器就已经估算出了两者的距离,是什么神奇的方法探索到这个奥秘的呢?
现实生活中,人们是怎样测量底部不可到达的建筑物高度的呢?又怎样在水平飞行的飞机上测量飞机下方山顶的海拔高度呢?在浩瀚无垠的海面上,航海人如何确保轮船不迷失方向,保持一定的航速和航向呢?1.仰角和俯角
与目标视线在同一铅垂平面内的水平线和目标视线的夹角,目标视线在水平线上方时叫________,目标视线在水平线下方时叫________,如图所示.仰角 俯角 2.视角
观察物体的两端视线张开的角度,叫做________.
3.坡角、坡比
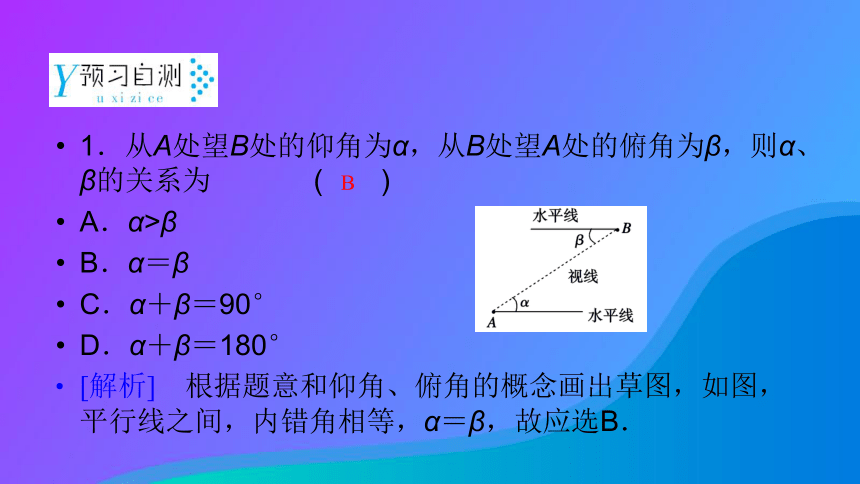
(1)坡角:坡面与__________的夹角.如下图中的角α.视角 水平面 1.从A处望B处的仰角为α,从B处望A处的俯角为β,则α、β的关系为 ( )
A.α>β
B.α=β
C.α+β=90°
D.α+β=180°
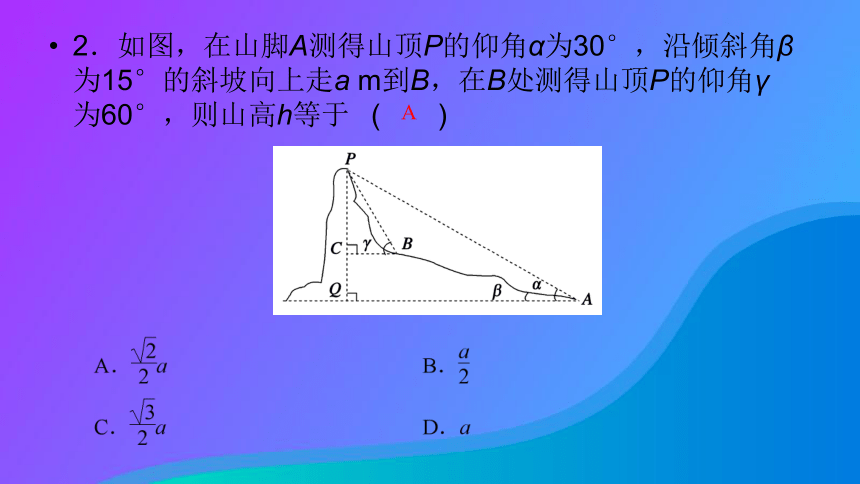
[解析] 根据题意和仰角、俯角的概念画出草图,如图,平行线之间,内错角相等,α=β,故应选B.B 2.如图,在山脚A测得山顶P的仰角α为30°,沿倾斜角β为15°的斜坡向上走a m到B,在B处测得山顶P的仰角γ为60°,则山高h等于 ( )A 30° 10 m 4.在点A处观察一物体的视角为50°,请画出示意图.互动探究学案命题方向1 ?利用仰角测量高度[分析] 如图所示,求角θ,必须把角θ、2θ、4θ和边长30、10尽量集中在一个三角形中,利用方程求解.例题 1『规律总结』 测量高度的方法
对于底部不可到达的建筑物的高度测量问题,由于不能直接通过解直角三角形解答,可通过构造含建筑物高度的三角形用正、余弦定理解答.构造三角形的方法常见的有:(1)取经过建筑物底部O的基线上两点A、B与顶部P构成Rt△PAO,Rt△PBO.(2)取与建筑物PD垂直,经过建筑物底部D的地平面上两点A、B与顶部P,底部D构成三角形,通过测量仰角及∠ADB,AB求解.D 命题方向2 ?利用俯角测量高度 如图所示,在山顶铁塔上B处测得地面上一点A的俯角为α,在塔底C处测得A处的俯角为β.已知铁塔BC部分的高为h,求出山高CD.
[分析] 为求山高CD,可解Rt△CAD,其中已知∠CAD=β,故只需再求出一条边长.由于已知BC=h,结合条件知可解△ABC,求得AC.例题 2『规律总结』 解决实际问题时,通常是从实际问题中抽象出一个或几个三角形,先解满足条件的三角形,再利用所得结果解其他三角形.2 km 命题方向3 ?测量角度问题 如图所示,当甲船位于A处时,获悉在其正东方向相距20 n mile的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10 n mile的C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到1°)?例题 3[点评] 为什么作辅助线CM?∠ACB并不是要求的结果,题目要求的方位角是北偏东多少度,需要作出正北方向线.在点C正北方向线与CB所成的角才是要求的角,即∠BCM.『规律总结』 航海问题是解三角形应用问题中的一类很重要的问题,解决这类问题一定要搞清所给的角,画出符合题意的图形,将所给距离和角度标在图中,然后分析可解的三角形及其与待求角问题的关系,确定解题步骤.〔跟踪练习3〕
我缉私巡逻艇在一小岛A南偏西50°的方向,距小岛A 12 n mile的B处,发现隐藏在小岛边上的一走私船正开始向岛北偏西10°方向行驶,测得其速度为每小时10 n mile,问我巡逻艇需用多大的速度朝什么方向航行才能恰在两个小时后截获该走私船?(参考数据:sin38°≈0.62)[解析] 如下图所示,AC所在射线即为走私船航行路线,假设我巡逻艇在C处截获走私船,我巡逻艇的速度为每小时x n mile,则BC=2x,AC=20.
依题意∠BAC=180°-50°-10°=120°, 已知A船在灯塔C北偏东80°处,距离灯塔C 2 km,B船在灯塔C北偏西40°,A、B两船的距离为3 km,求B到C的距离.例题 4[错解] 如图所示,
由题意知AB=3 km,AC=2 km,∠ACB=120°.[辨析] 错解中忽视了边AB为最大边,故BC[分析] 本题中所涉及的路程在不断变化,但舰艇和渔轮相遇时所用时间相等,先设出所用时间t,找出等量关系,然后解三角形.例题 5不确定航向的角度问题1.如图,在离地面高400 m的热气球上,观测到山顶C处的仰角为15°,山脚A处的俯角为45°.已知∠BAC=60°,则山的高度BC为 ( )
A.700 m
B.640 m
C.600 m
D.560 mC 2.如图,从气球A测得济南全运会东荷、西柳两个场馆B、C的俯角分别为α、β,此时气球的高度为h,则两个场馆B、C间的距离为 ( )B 4.A、B是水平面上的两个点,相距800 m,在A点测得山顶C的仰角为45°,∠BAD=120°,又在B点测得∠ABD=45°,其中点D是点C在水平面的垂足,求山高CD.
[解析] 如图,因为CD⊥平面ABD,∠CAD=45°,所以CD=AD.
现实生活中,人们是怎样测量底部不可到达的建筑物高度的呢?又怎样在水平飞行的飞机上测量飞机下方山顶的海拔高度呢?在浩瀚无垠的海面上,航海人如何确保轮船不迷失方向,保持一定的航速和航向呢?1.仰角和俯角
与目标视线在同一铅垂平面内的水平线和目标视线的夹角,目标视线在水平线上方时叫________,目标视线在水平线下方时叫________,如图所示.仰角 俯角 2.视角
观察物体的两端视线张开的角度,叫做________.
3.坡角、坡比
(1)坡角:坡面与__________的夹角.如下图中的角α.视角 水平面 1.从A处望B处的仰角为α,从B处望A处的俯角为β,则α、β的关系为 ( )
A.α>β
B.α=β
C.α+β=90°
D.α+β=180°
[解析] 根据题意和仰角、俯角的概念画出草图,如图,平行线之间,内错角相等,α=β,故应选B.B 2.如图,在山脚A测得山顶P的仰角α为30°,沿倾斜角β为15°的斜坡向上走a m到B,在B处测得山顶P的仰角γ为60°,则山高h等于 ( )A 30° 10 m 4.在点A处观察一物体的视角为50°,请画出示意图.互动探究学案命题方向1 ?利用仰角测量高度[分析] 如图所示,求角θ,必须把角θ、2θ、4θ和边长30、10尽量集中在一个三角形中,利用方程求解.例题 1『规律总结』 测量高度的方法
对于底部不可到达的建筑物的高度测量问题,由于不能直接通过解直角三角形解答,可通过构造含建筑物高度的三角形用正、余弦定理解答.构造三角形的方法常见的有:(1)取经过建筑物底部O的基线上两点A、B与顶部P构成Rt△PAO,Rt△PBO.(2)取与建筑物PD垂直,经过建筑物底部D的地平面上两点A、B与顶部P,底部D构成三角形,通过测量仰角及∠ADB,AB求解.D 命题方向2 ?利用俯角测量高度 如图所示,在山顶铁塔上B处测得地面上一点A的俯角为α,在塔底C处测得A处的俯角为β.已知铁塔BC部分的高为h,求出山高CD.
[分析] 为求山高CD,可解Rt△CAD,其中已知∠CAD=β,故只需再求出一条边长.由于已知BC=h,结合条件知可解△ABC,求得AC.例题 2『规律总结』 解决实际问题时,通常是从实际问题中抽象出一个或几个三角形,先解满足条件的三角形,再利用所得结果解其他三角形.2 km 命题方向3 ?测量角度问题 如图所示,当甲船位于A处时,获悉在其正东方向相距20 n mile的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10 n mile的C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到1°)?例题 3[点评] 为什么作辅助线CM?∠ACB并不是要求的结果,题目要求的方位角是北偏东多少度,需要作出正北方向线.在点C正北方向线与CB所成的角才是要求的角,即∠BCM.『规律总结』 航海问题是解三角形应用问题中的一类很重要的问题,解决这类问题一定要搞清所给的角,画出符合题意的图形,将所给距离和角度标在图中,然后分析可解的三角形及其与待求角问题的关系,确定解题步骤.〔跟踪练习3〕
我缉私巡逻艇在一小岛A南偏西50°的方向,距小岛A 12 n mile的B处,发现隐藏在小岛边上的一走私船正开始向岛北偏西10°方向行驶,测得其速度为每小时10 n mile,问我巡逻艇需用多大的速度朝什么方向航行才能恰在两个小时后截获该走私船?(参考数据:sin38°≈0.62)[解析] 如下图所示,AC所在射线即为走私船航行路线,假设我巡逻艇在C处截获走私船,我巡逻艇的速度为每小时x n mile,则BC=2x,AC=20.
依题意∠BAC=180°-50°-10°=120°, 已知A船在灯塔C北偏东80°处,距离灯塔C 2 km,B船在灯塔C北偏西40°,A、B两船的距离为3 km,求B到C的距离.例题 4[错解] 如图所示,
由题意知AB=3 km,AC=2 km,∠ACB=120°.[辨析] 错解中忽视了边AB为最大边,故BC
A.700 m
B.640 m
C.600 m
D.560 mC 2.如图,从气球A测得济南全运会东荷、西柳两个场馆B、C的俯角分别为α、β,此时气球的高度为h,则两个场馆B、C间的距离为 ( )B 4.A、B是水平面上的两个点,相距800 m,在A点测得山顶C的仰角为45°,∠BAD=120°,又在B点测得∠ABD=45°,其中点D是点C在水平面的垂足,求山高CD.
[解析] 如图,因为CD⊥平面ABD,∠CAD=45°,所以CD=AD.
