人教版七年级下册6.3 实数 课件(共15张PPT)
文档属性
| 名称 | 人教版七年级下册6.3 实数 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-27 14:28:19 | ||
图片预览






文档简介
你还记得如何把下面的数进行分类吗?
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
无限不循环的小数叫做无理数.
你能举出一些无理数吗?zxxk
无理数也有正负之分,例如:
正无理数:
负无理数:
把下列各数分别填入相应的集合内:
有理数集合
无理数集合
2.开不尽方的数
3.有一定的规律,但
不循环的无限小数。
无理数的特征:
注意:带根号的数不一定是无理数
有理数和无理数统称实数.
无限不循环小数叫做无理数
( 强调: 无限 、 不循环.)
无理数常见的4种典型:
(3)、无限不循环小数:0.101001000…(两个
“1”之间依次多一个0)
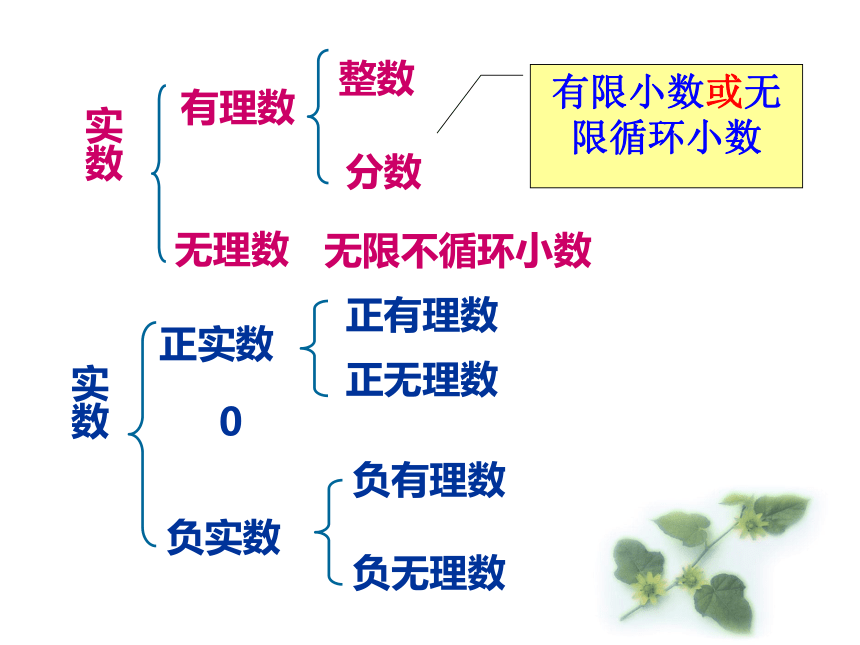
实数
实数
有理数
无理数
整数
分数
无限不循环小数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
有限小数或无限循环小数
一、判断:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
6.两个无理数之积不一定是无理数。( )
7.两个无理数之和一定是无理数。( )
×
×
×
8.有理数与无理数之和一定是无理数 ( )
每个有理数都可以用数轴上的点表示,那么无理数 是否也可以用数轴上的点来表示呢?
π
直径为1的圆
(1)如下图,以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么?
(2)如果将所有有理数都标到数轴上,那么数轴 填满吗?
B
A
每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数。即实数和数轴上的点是一一对应的。Z,xxk
C
在数轴上表示的两个实数,右边的数总比左边的数大。
数轴上的点有些
表示有理数,有
些表示无理数.
有理数能不能将数轴排满?
每个实数都可以用数轴上的
一个点来表示;反过来,数轴上的每一个点都表示一个实数.
数轴上一个点
有一个实数
有一个实数
数轴上一个点
即实数和数轴上点是一一对应的.
习题6.3
1题,2题
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
无限不循环的小数叫做无理数.
你能举出一些无理数吗?zxxk
无理数也有正负之分,例如:
正无理数:
负无理数:
把下列各数分别填入相应的集合内:
有理数集合
无理数集合
2.开不尽方的数
3.有一定的规律,但
不循环的无限小数。
无理数的特征:
注意:带根号的数不一定是无理数
有理数和无理数统称实数.
无限不循环小数叫做无理数
( 强调: 无限 、 不循环.)
无理数常见的4种典型:
(3)、无限不循环小数:0.101001000…(两个
“1”之间依次多一个0)
实数
实数
有理数
无理数
整数
分数
无限不循环小数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
有限小数或无限循环小数
一、判断:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
6.两个无理数之积不一定是无理数。( )
7.两个无理数之和一定是无理数。( )
×
×
×
8.有理数与无理数之和一定是无理数 ( )
每个有理数都可以用数轴上的点表示,那么无理数 是否也可以用数轴上的点来表示呢?
π
直径为1的圆
(1)如下图,以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么?
(2)如果将所有有理数都标到数轴上,那么数轴 填满吗?
B
A
每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数。即实数和数轴上的点是一一对应的。Z,xxk
C
在数轴上表示的两个实数,右边的数总比左边的数大。
数轴上的点有些
表示有理数,有
些表示无理数.
有理数能不能将数轴排满?
每个实数都可以用数轴上的
一个点来表示;反过来,数轴上的每一个点都表示一个实数.
数轴上一个点
有一个实数
有一个实数
数轴上一个点
即实数和数轴上点是一一对应的.
习题6.3
1题,2题
