高中数学第3章空间向量与立体几何3.1.1空间向量及其线性运算课件5苏教版选修2_1(30张PPT)
文档属性
| 名称 | 高中数学第3章空间向量与立体几何3.1.1空间向量及其线性运算课件5苏教版选修2_1(30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-27 15:53:03 | ||
图片预览










文档简介
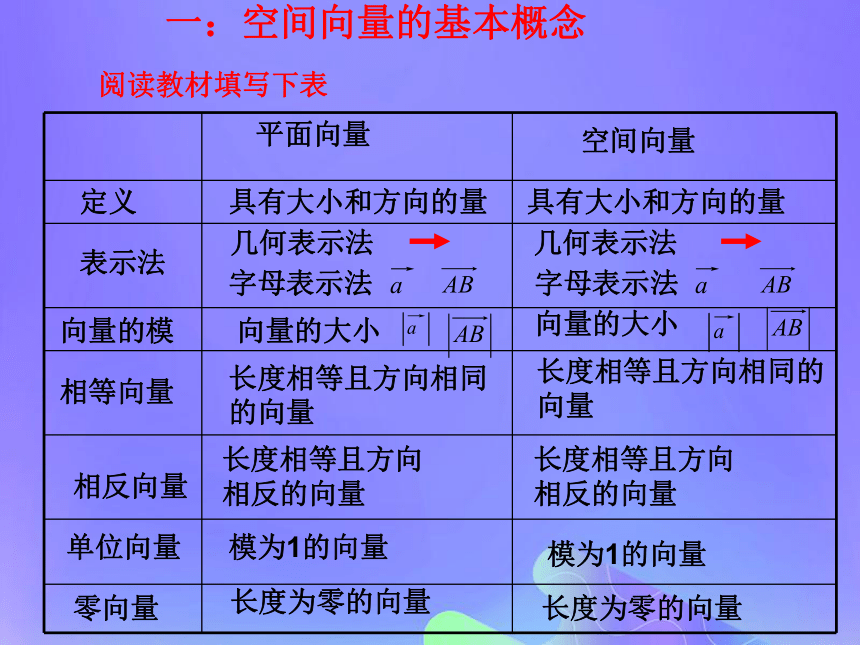
课件30张PPT。空间向量及其运算从建筑物上找向量的影子在空间里既有大小又有方向的量叫做空间向量。阅读教材填写下表平面向量空间向量具有大小和方向的量具有大小和方向的量 几何表示法几何表示法字母表示法 字母表示法 向量的大小 向量的大小 长度为零的向量 长度为零的向量模为1的向量模为1的向量长度相等且方向
相反的向量长度相等且方向
相反的向量长度相等且方向相同 的向量长度相等且方向相同的向量定义表示法向量的模零向量单位向量相反向量相等向量一:空间向量的基本概念例1、给出以下命题:
(1)两个空间向量相等,则它们的起点、终点相同;
(2)若空间向量 满足 ,则 ;
(3)在正方体 中,必有 ;
(4)若空间向量 满足 ,则 ;
(5)空间中任意两个单位向量必相等。
其中不正确命题的个数是———————— (1)(2)(5)3OAB结论:空间任意两个向量都可以平移到同一个平面内,
,成为同一平面内的两个向量。思考:平面是否唯一?探究一:空间任意两个向量是否都可以平移到同一平面内?为什么?O′结论:空间任意两个向量都是共面向量,所以它们可用同一平面内的两条有向线段表示。因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们。平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
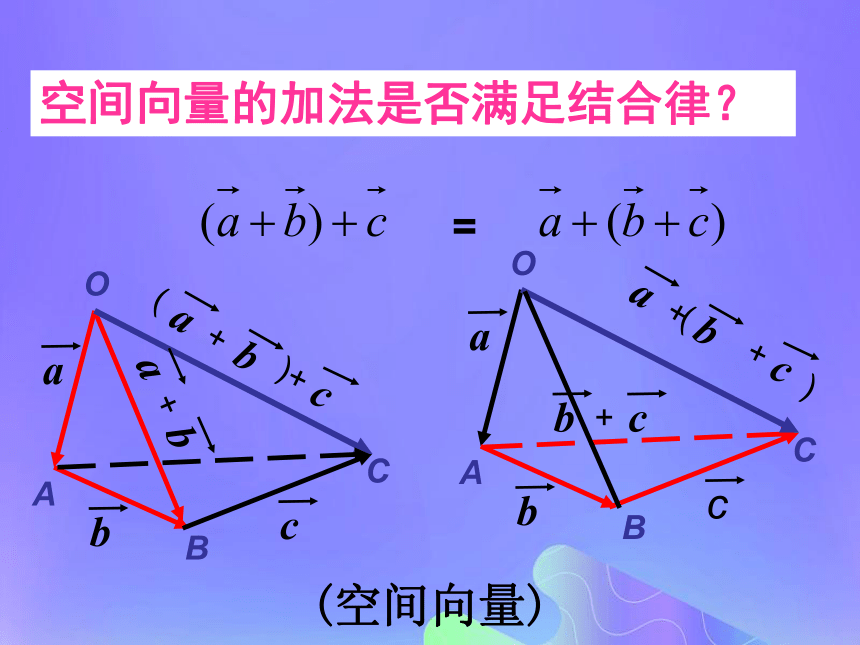
平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律OABC探究二:空间向量如何进行加减运算?空间向量的数乘OABC空间向量加法交换律:探究三:空间向量的加法是否满足交换律?b + aa + b
=OABCOABC(空间向量)空间向量的加法是否满足结合律?=加法交换律:加法结合律:空间向量的加法的运算律:数乘分配律平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律加法交换律数乘分配律加法:三角形法则或
平行四边形法则减法:三角形法则加法结合律AB规定零向量与任何向量共线空间向量共线定理:对于空间任意的两个向量,a,b,(a≠0),b与a共线的充要条件是存在实数λ,使b= λ aABB零向量的方向是任意的如何理解零向量的方向?共线向量:零向量与任意向量共线.共面向量:1.共面向量:能平移到同一平面的向量,叫做共面向量.注意:空间任意两个向量是共面的,但空间任意三个向量就不一定共面的了。 平面向量基本定理的内容存 在 性唯 一 性如果是同一平面内的两个不共线向量,那么对于这一平面的任意向量一对实数,使有且只有2.共面向量定理 :如果两个向量
不共线,则向量 与向量 共面的充要
条件是存在实数对 使 推论:空间一点P位于平面MAB内的充要条件是存在有序实数对x,y使
或对空间任一点O,有
例题1.如图所示,已知矩形ABCD和矩形ADEF所在平面互相垂直,点M,N分别在对角线BD,AE上,且求证:MN∥平面CBEGH例2 对空间任意一点O和不共线的三点
A、B、C,试问满足向量关系式
(其中 )的四点P、A、B、
C是否共面?例3 已知A、B、M三点不共线,对于平面
ABM外的任一点O,确定在下列各条件下,
点P是否与A、B、M一定共面?
已知E、F、G、H分别是空间
四边形ABCD的边AB、BC、CD、DA
的中点,
(1)求证:E、F、G、H四点共面;
(2)求证:BD∥平面EFGH;
(1)要证E、F、G、H四点共面,可
寻求x,y使
(2)由向量共线得到线线平行,进而得到线面
平行.练习3证明 (1)连接BG,则
由共面向量定理的推论知:
E、F、G、H四点共面.
(2)因为
所以EH∥BD.
又EH?平面EFGH,BD?平面EFGH,
所以BD∥平面EFGH.复习平面向量的基本定理如果 , 是平面内两个不共线向量,那么对于这一平面内的任一向量 ,有且只有
一对实数t1,t2,使 OCMN对向量 进行分解:空间任一向量能用三个不共面的向量来线性表示吗?二、空间向量的基本定理:如果三个向量 不共面,那么对空间任一向量 ,存在一个唯
一的有序实数组(x,y,z),使ABDCO思路:作E 如果三个向量 不共面,那么空间的每一个向量都可由向量 线性表示.把 称为空间的一个基底基底:基向量: 如果空间一个基底的三个向量是两两互相垂直,那么这个基底叫做正交基底. 正交基底:单位正交基底: 当一个正交基底的三个基向量都是单位向量时,称这个基底为单位正交基底. 通常用 表示 设点O、A、B、C是不共面的四点,则对空间任一点P,都存在唯一的有序实数组( x,y,z),使
OABCPPP注:空间任意三个不共面向量都可以构成空间的一个基底
如:推论:例:已知空间四边形OABC,对角线OB、AC,M和N分别是OA、BC的中点,点G在MN上,且使MG=2GN,试用基底 表示向量OABCMNG解:在△OMG中,
相反的向量长度相等且方向
相反的向量长度相等且方向相同 的向量长度相等且方向相同的向量定义表示法向量的模零向量单位向量相反向量相等向量一:空间向量的基本概念例1、给出以下命题:
(1)两个空间向量相等,则它们的起点、终点相同;
(2)若空间向量 满足 ,则 ;
(3)在正方体 中,必有 ;
(4)若空间向量 满足 ,则 ;
(5)空间中任意两个单位向量必相等。
其中不正确命题的个数是———————— (1)(2)(5)3OAB结论:空间任意两个向量都可以平移到同一个平面内,
,成为同一平面内的两个向量。思考:平面是否唯一?探究一:空间任意两个向量是否都可以平移到同一平面内?为什么?O′结论:空间任意两个向量都是共面向量,所以它们可用同一平面内的两条有向线段表示。因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们。平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律OABC探究二:空间向量如何进行加减运算?空间向量的数乘OABC空间向量加法交换律:探究三:空间向量的加法是否满足交换律?b + aa + b
=OABCOABC(空间向量)空间向量的加法是否满足结合律?=加法交换律:加法结合律:空间向量的加法的运算律:数乘分配律平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律加法交换律数乘分配律加法:三角形法则或
平行四边形法则减法:三角形法则加法结合律AB规定零向量与任何向量共线空间向量共线定理:对于空间任意的两个向量,a,b,(a≠0),b与a共线的充要条件是存在实数λ,使b= λ aABB零向量的方向是任意的如何理解零向量的方向?共线向量:零向量与任意向量共线.共面向量:1.共面向量:能平移到同一平面的向量,叫做共面向量.注意:空间任意两个向量是共面的,但空间任意三个向量就不一定共面的了。 平面向量基本定理的内容存 在 性唯 一 性如果是同一平面内的两个不共线向量,那么对于这一平面的任意向量一对实数,使有且只有2.共面向量定理 :如果两个向量
不共线,则向量 与向量 共面的充要
条件是存在实数对 使 推论:空间一点P位于平面MAB内的充要条件是存在有序实数对x,y使
或对空间任一点O,有
例题1.如图所示,已知矩形ABCD和矩形ADEF所在平面互相垂直,点M,N分别在对角线BD,AE上,且求证:MN∥平面CBEGH例2 对空间任意一点O和不共线的三点
A、B、C,试问满足向量关系式
(其中 )的四点P、A、B、
C是否共面?例3 已知A、B、M三点不共线,对于平面
ABM外的任一点O,确定在下列各条件下,
点P是否与A、B、M一定共面?
已知E、F、G、H分别是空间
四边形ABCD的边AB、BC、CD、DA
的中点,
(1)求证:E、F、G、H四点共面;
(2)求证:BD∥平面EFGH;
(1)要证E、F、G、H四点共面,可
寻求x,y使
(2)由向量共线得到线线平行,进而得到线面
平行.练习3证明 (1)连接BG,则
由共面向量定理的推论知:
E、F、G、H四点共面.
(2)因为
所以EH∥BD.
又EH?平面EFGH,BD?平面EFGH,
所以BD∥平面EFGH.复习平面向量的基本定理如果 , 是平面内两个不共线向量,那么对于这一平面内的任一向量 ,有且只有
一对实数t1,t2,使 OCMN对向量 进行分解:空间任一向量能用三个不共面的向量来线性表示吗?二、空间向量的基本定理:如果三个向量 不共面,那么对空间任一向量 ,存在一个唯
一的有序实数组(x,y,z),使ABDCO思路:作E 如果三个向量 不共面,那么空间的每一个向量都可由向量 线性表示.把 称为空间的一个基底基底:基向量: 如果空间一个基底的三个向量是两两互相垂直,那么这个基底叫做正交基底. 正交基底:单位正交基底: 当一个正交基底的三个基向量都是单位向量时,称这个基底为单位正交基底. 通常用 表示 设点O、A、B、C是不共面的四点,则对空间任一点P,都存在唯一的有序实数组( x,y,z),使
OABCPPP注:空间任意三个不共面向量都可以构成空间的一个基底
如:推论:例:已知空间四边形OABC,对角线OB、AC,M和N分别是OA、BC的中点,点G在MN上,且使MG=2GN,试用基底 表示向量OABCMNG解:在△OMG中,
