6.3 万有引力定律

人教版物理必修2-第六章——万有引力

一、开普勒定律
(
知识点睛
)

浩瀚宇宙，星移斗转，星体的运动和演化都遵循一定的规律，人类对这种规律的正确认识经历了漫长而曲折的过程。
1．人类对行星运动规律的认识过程
当我们远古的祖先惊叹星空的玄妙时，他们就开始试图破译日月星辰等天文现象的奥秘……公元前4世纪，亚里士多德认为，宇宙是一个有限的球体，分为天地两层，地球位于宇宙中心，所以日月围绕地球运行，物体总是落向地面。地球之外有9个等距天层，由里到外的排列次序是：月球天、水星天、金星天、太阳天、火星天、木星天、土星天、恒星天和原动力天，除此之外空无一物。众神在原动力天推动了恒星天层，才带动了所有天层的运动。
我们的祖先发现，尽管所有星辰每日都要东升西落，但绝大多数星辰的相互位置都几乎是固定的，几百年内不会发生肉眼可见的变化，它们是“恒星”。然而，水星、金星、火星、木星、土星这五颗亮星则在众星的背景前移动，有的在几个星期中就能发现它的位置变化，所以它们叫“行星”。
细心的观察表明，行星并非总向一个方向移动。大多数时间它由西向东相对于恒星移动，但有时却要停下来，然后向西移动一段时间，随后又向东移动，这个现象叫做行星的逆行。

火星的退行
为了解释行星的逆行，希腊人提出一个理论。这个理论认为每个行星都沿着圆运动，这个圆叫做“本轮”，同时本轮的圆心又环绕着地球沿一个叫做均轮的大圆运动。这个理论在公元2世纪由伟大的古代天文学家托勒密完善而成。

值得指出的是，一个本轮与一个均轮还不能十分准确地解释行星的运动。为了与观察结果更好地符合，每个行星需要不止一个本轮，结果托勒密在本轮上再加一层又一层的本轮，“轮上轮”的总数达到多个，并且还要引入“偏心点”和“偏心等距点”等复杂概念。尽管这个理论非常复杂，但它却能算出行星以前的位置，并相当准地预言它们未来的位置。于是，托勒密地心体系一代又一代的传下去，直到世纪，未发生重大变化。

宇宙的地心体系
然而，托勒密的理论十分繁杂，使它缺少简洁性，而简洁性正是科学家们所追求的。波兰天文学家哥白尼坚信宇宙与自然是美的，而美的东西一定是简单和谐的，托勒密的宇宙图景与他的信念不一致。这个时期，文艺复兴解脱了束缚人们头脑的枷锁，哥白尼采取了比前人更广阔的视角来洞察自然。哥白尼的眼光超越了地球。他把地球看成空间中的一个物体，一个与其他天体相似的物体。这个观念是如此开放，以至在他面前，地球中心宇宙观显得那么狭隘和偏执。
哥白尼提出，行星和地球绕太阳做匀速圆周运动，只有月亮环绕地球运行。由于地球的自转，我们看到了太阳、月亮和众星每天由东向西的运动。这个理论也解释了行星逆行等许多现象。于是，他动情地写道：“太阳在宇宙正中坐在其宝座上。在这壮丽的神殿里，有谁能将这个发光体放在一个更好的位置上以让它同时普照全宇宙？……于是我们在这样的安排中找到了这个世界美妙的和谐……”。年哥白尼临终前在病榻上为其毕生致力的著作《天体运行论》印出的第一本书签上了自己的姓名。这部书预示了地心宇宙论的终结。
到了世纪初，伽利略发明了望远镜。年，他发现了围绕木星转动的“月球”，进一步表明地球不是所有天体运动的中心。至于是什么维持地球运动、空中的飞鸟和浮云为什么不落在地面 等问题，直到伽利略和牛顿提出关于运动的新观念之后，才得到合理的解释。
哥白尼去世三年后，第谷·布拉赫在丹麦出生，他把全身心都投入到行星位置的测量中。在他以前，人们测量天体位置的误差大约是，而第谷把这个误差减小到。他观测的结果为哥白尼的学说提供了关键性的支持。
年开普勒在德国出生，年开始与第谷一起工作，他善于从理论上思考问题。开普勒相信哥白尼的学说，在第谷去世之后，他以全部的精力整理第谷的观测数据，企求求得行星运动轨迹的最准确描述。经过多年的尝试性计算，终于发现并先后于年和年发表了行星运动的三个定律，后人称作开普勒行星运动定律。
（对开普勒的研究工作感兴趣的同学，可以阅读《新概念物理教程·力学》的相关内容或查阅其他资料）

托勒密 哥白尼 第谷 开普勒
2．开普勒的行星运动规律
⑴ 开普勒第一定律：
当第谷移居布拉格时，一位29岁的德国人——开普勒成了他的助手。1601年第谷去世后，开普勒继承了老师30年富有成效的观察结果。他在研究了这些数据后，认为可以利用几何学和数学知识来解释这些行星的距离和运动。开普勒相信，太阳对行星施加力的作用，并将太阳至于系统的中心地位。通过数年对第谷关于火星数据的仔细研究，开普勒发现了能概括所有行星和卫星运动的定律。
开普勒第一定律指出：所有行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上。

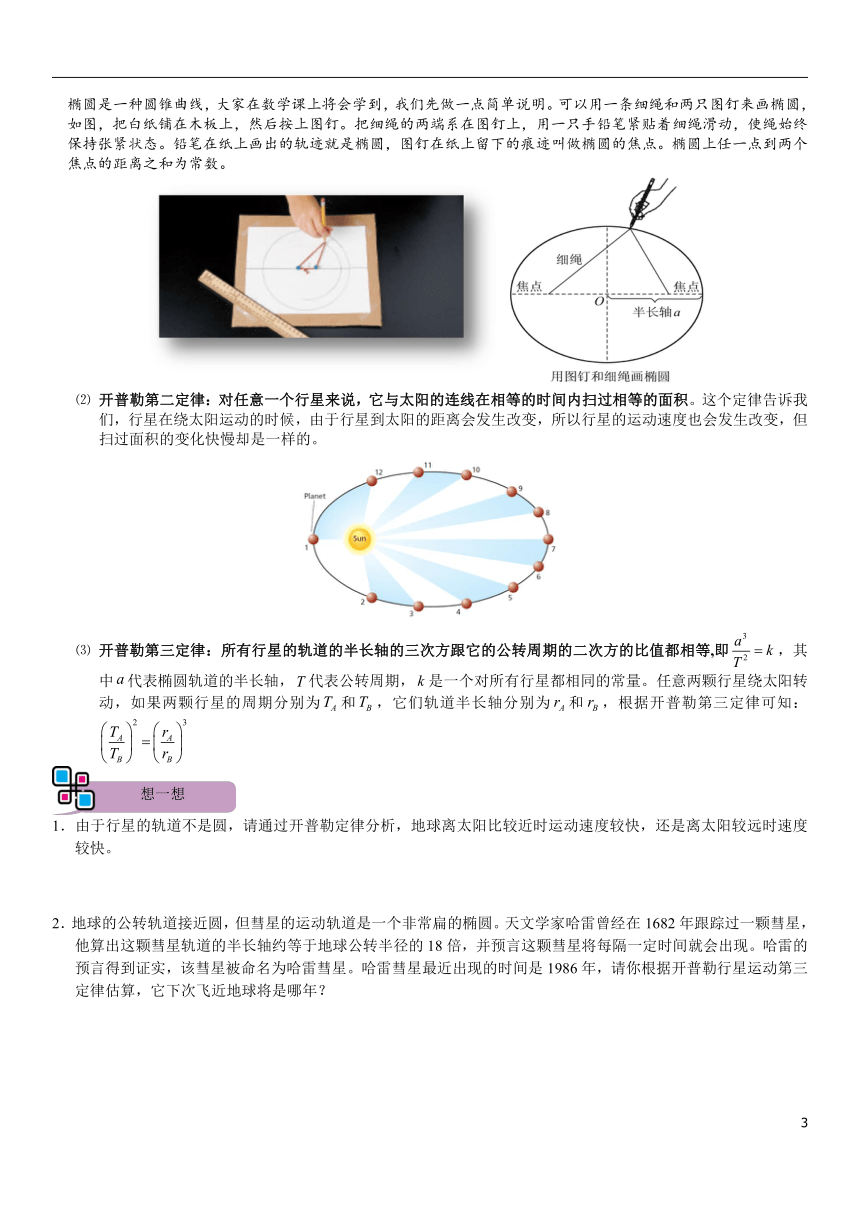
椭圆是一种圆锥曲线，大家在数学课上将会学到，我们先做一点简单说明。可以用一条细绳和两只图钉来画椭圆，如图，把白纸铺在木板上，然后按上图钉。把细绳的两端系在图钉上，用一只手铅笔紧贴着细绳滑动，使绳始终保持张紧状态。铅笔在纸上画出的轨迹就是椭圆，图钉在纸上留下的痕迹叫做椭圆的焦点。椭圆上任一点到两个焦点的距离之和为常数。

⑵ 开普勒第二定律：对任意一个行星来说，它与太阳的连线在相等的时间内扫过相等的面积。这个定律告诉我们，行星在绕太阳运动的时候，由于行星到太阳的距离会发生改变，所以行星的运动速度也会发生改变，但扫过面积的变化快慢却是一样的。

⑶ 开普勒第三定律：所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等,即，其中代表椭圆轨道的半长轴，代表公转周期，是一个对所有行星都相同的常量。任意两颗行星绕太阳转动，如果两颗行星的周期分别为和，它们轨道半长轴分别为和，根据开普勒第三定律可知：
(
想一想
)
1．由于行星的轨道不是圆，请通过开普勒定律分析，地球离太阳比较近时运动速度较快，还是离太阳较远时速度较快。



2．地球的公转轨道接近圆，但彗星的运动轨道是一个非常扁的椭圆。天文学家哈雷曾经在1682年跟踪过一颗彗星，他算出这颗彗星轨道的半长轴约等于地球公转半径的18倍，并预言这颗彗星将每隔一定时间就会出现。哈雷的预言得到证实，该彗星被命名为哈雷彗星。哈雷彗星最近出现的时间是1986年，请你根据开普勒行星运动第三定律估算，它下次飞近地球将是哪年？


(
例题精讲
)
下列说法正确的是
A．太阳系中的八大行星有一个共同的轨道焦点
B．行星的运动方向总是沿着轨道的切线方向
C．行星的运动方向总是与它和太阳的连线垂直
D．太阳是静止不动的
AB

题型：开普勒第二定律
某行星绕太阳运行的椭圆轨道如图所示，和是椭圆轨道的两个焦点，行星在点的速率比在点的速率大，则太阳是位于
A． B． C． D．
A


题型：开普勒第三定律
关于开普勒第三定律，下列理解中正确的是
A．是一个与行星无关的常量
B．代表行星运动的轨道半径
C．代表行星运动的自转周期
D．代表行星绕太阳运动的公转周期
AD

太空探测器进入了一个圆形轨道绕太阳运转，已知其轨道半径为地球绕太阳运转轨道半径的9倍，则太空探测器绕太阳运转的周期是
A．3年 B．9年 C．27年 D．81年
C


二、万有引力
(
知识点睛
)
1．太阳与行星间的引力
开普勒定律发现之后，人们开始更深入地思考——是什么原因使行星绕太阳运动？许多科学家都对此问题提出过自己的解释。
开普勒认为行星的运动是由于太阳磁力吸引的缘故，磁力与距离成反比；
伽利略认为行星的运动与地面物体的运动遵从不同的规律，行星运动是由“惯性”自行维持的；
笛卡尔认为宇宙由不停旋转着的微粒所组成，微粒的运动形成漩涡。太阳和行星在各自的漩涡中心。行星漩涡带动卫星运动，太阳的漩涡带动行星和卫星一起运动；
胡克认为行星的运动是太阳引力的缘故，并且引力的大小与到太阳距离的平方成反比，重力是由地球引力产生的；
牛顿在前人对惯性研究的基础上，开始思考“物体怎样才会不沿直线运动”这一问题。他认为以任何方式改变速度（包括方向）都需要力，因此，使行星沿圆或椭圆运动，需要指向圆心或椭圆焦点的力，这个力就是太阳对它的引力。于是，牛顿利用他的运动定律把行星的向心加速度与太阳对它的引力联系起来了。
下面，我们追寻牛顿的思路，在开普勒定律的基础上，来探究太阳与行星之间的引力。由于行星的轨道与圆十分接近，为了简化问题，我们把行星的轨道当作圆来处理。

此图为太阳系中各个行星运动轨道的比例图
⑴ 太阳对行星的引力
根据开普勒第一、第二定律可知，行星以太阳为圆心做匀速圆周运动。太阳对行星的引力，就等于行星做匀速圆周运动所需的向心力。
设行星的质量是，速度是，行星到太阳的距离是，则行星绕太阳做匀速圆周运动的向心力为；
天文观测难以观测行星运行的速度，但容易观测其公转周期。将代入向心力的表达式，可得；
将开普勒第三定律代入得：。
在这个式子中，等号右边除了，以外，其余都是常量，对任何行星来说都是相同的。因此可以说太阳对行星的引力与成正比，即。
⑵ 行星对太阳的引力
就太阳对行星的引力来说，行星是受力星体。因此可以说，是与受力星体的质量成正比的。然而，从太阳与行星间相互作用的角度来看，两者的地位是相同的。也就是说，既然太阳吸引行星，行星也必然吸引太阳。因此，行星对太阳的引力也应该与太阳的质量成正比。即。
⑶ 太阳与行星间的引力
由于，，且。所以，我们可以概括地说，太阳与行星间引力的大小与太阳的质量、行星的质量成正比，与两者距离的二次方成正比，即。写成等式就是。与太阳、行星均无关，是一个常量。
太阳与行星间引力的方向沿着二者的连线。
2．万有引力定律
通过上面的分析，我们已经知道了太阳与行星之间作用力的规律，并能完全解释行星的运动了。在此基础上，我们可以进一步设想：太阳与行星之间的引力使得行星不能飞离太阳，那么是什么力使得地面的物体不离开地球呢？也就是说，地球使物体下落的力与地球、太阳之间的引力是不是同一种力呢？即使在最高的山顶上，物体的重力也没有明显的减弱，那么这个力必定延伸到远得多的地方，它会不会作用在月球上？拉住月球使其做圆周运动的力与拉着苹果下落的力，以及地球、众行星与太阳之间的作用力，会不会是同一种力，遵循着相同的规律？这些想法的正确性要由事实来检验。
⑴ 月——地检验
假定维持月球绕地球运动的力与使得苹果下落的力真的是同一种力，同样遵从“平方反比”的规律，那么，由于月球轨道半径约为地球半径的倍，所以月球轨道上一个物体受到的引力，比它在地面附近时受到的引力要小，前者只有后者的。根据牛顿第二定律，物体在月球轨道上运动的加速度也就应该大约是它在地面附近下落时的加速度（自由落体加速度）的。
在牛顿的时代，自由落体加速度已经能够比较精确地测定，当时也能比较精确地测定月球与地球的距离、月球的公转周期，从而能够算出月球运动的向心加速度。
让我们实际计算一下：月球围绕地球的公转周期天，地球半径约为，计算出月球围绕地球做圆周运动的向心加速；物体在地面处的重力加速度，。
计算结果与预期符合的很好，这表明，地面物体所受地球的引力、月球所受地球的引力，遵从相同的规律。
⑵ 万有引力定律
我们的思想还可以更解放一点，既然太阳与行星之间、地球与月球之间、地球与地面物体之间具有“与两个物体的质量成正比，与它们之间距离的二次方成反比”的吸引力，是否任意两个物体之间都有这样的力呢？很可能有，只是由于身边的物体比天体的质量小的多，不易察觉罢了。于是我们可以大胆的把以上结论推广到宇宙的一切物体之间。
自然界中任何两个物体都相互吸引，引力的方向在它们的连线上，引力的大小与物体的质量和的乘积成正比，与它们之间距离的二次方成反比，即

式中质量的单位用，距离的单位用，力的单位用。是比例系数，叫做引力常量，适用于任何两个物体。
经过大量事实的直接或间接的检验，上述猜想成为科学史上最伟大的规律之一——万有引力定律。
⑶ 万有引力常量
牛顿得出了万有引力与物体质量及他们之间距离的关系，但却无法计算出两个天体之间万有引力的大小，因为他不知道引力常量。由于是一个很小的数值，而当时又缺少精密测量仪器。直到1798年，英国物理学家卡文迪许才首先做出了精确测量。目前推荐的标准值为，通常取。
⑷ 万有引力定律的适用条件
① 当两个物体间的距离远远大于每个物体的尺寸时，物体可以看成质点，它们之间的引力可直接使用万有引力定律公式计算。
② 通过严格的理论分析得到，质量分布均匀的球体，它们之间的引力也可直接使用公式计算，这时是两球心间的距离。
****************************************************************************************
在万有引力定律发表大约100年后，英国的米切尔首先设计了一种专门来进行引力实验的仪器，称为扭秤。这个装置的特点是通过测量微小的扭转角度，以显示微弱的引力，从而使在实验室中测定引力常量成为可能。但是米切尔没有亲自做过测定引力常量的实验，因为在扭秤还没有制造完时，他就去世了。
年，卓越的英国物理学家卡文迪许在米切尔的基础上完成了扭秤的制作，而且做了重要的改进。
卡文迪许用一个质量大的铁球和一个质量小的铁球分别放在扭秤的两端。扭秤中间用一根韧性很好的钢丝系在支架上，钢丝上有个小镜子。用激光照射镜子，激光反射到一个很远的地方，标记此时激光所在的点。用两个质量一样的铁球同时分别吸引扭秤上的两个铁球。由于万有引力作用，扭秤微微偏转，但激光所反射的远点却移动了较大的距离。他由此计算出了万有引力公式中的常数。此实验的巧妙之处在于将微弱的力的作用进行了放大。


卡文迪许实验
****************************************************************************************
(
想一想
)
1．在太阳系中，开普勒第三定律中是一个对所有行星都相同的常量，请结合万有引力定律说明值与太阳的质量有关。


(
例题精讲
)

题型：万有引力的概念理解
根据开普勒定律和圆周运动的知识可知，太阳对行星的引力，行星对太阳的引力，其中、、分别为太阳质量、行星质量和太阳与行星间的距离。下列说法正确的是
A．由和知
B．和大小相等，是作用力与反作用力
C．和大小相等，是同一个力
D．太阳对行星的引力提供行星绕太阳做圆周运动的向心力
BD


对于万有引力定律的数学表达式，下列说法中正确的是
A．公式中为引力常量，是人为规定的
B．受到的万有引力总是大小相等
C．受到的万有引力是一对平衡力
D．受到的万有引力是作用力与反作用力
BD

题型：万有引力简单计算
两位质量各为的人相距时，他们之间的万有引力大小的数量级约为
A． B． C． D．
A
如图所示，两球的半径远小于，而球质量均匀分布，质量为、，则两球间的万有引力大小为
A． B．
C． D．
D


（我国已经成功地向太空发射了“神舟”号载人飞船。如果“神舟”号飞船由地球飞向月球，地球的质量约为月球质量的倍，那么，当地球对它的引力和月球对它的引力大小相等时，求此时飞船距地心的距离与距月心的距离的比值。


在讨论地球潮汐成因时，地球绕太阳运行轨道与月球绕地球运行轨道可视为圆轨道．已知太阳质量约为月球质量的倍，地球绕太阳运行的轨道半径约为月球绕地球运行的轨道半径的倍．关于太阳和月球对地球上相同质量海水的引力，以下说法正确的是
A．太阳引力远大于月球引力
B．太阳引力与月球引力相差不大
C．月球对不同区域海水的吸引力大小相等
D．月球对不同区域海水的吸引力大小有差异
AD
****************************************************************************************
此题可作为老师们的补充题
1、两个物体之间的万有引力大小为，若两物体之间的距离减小，两物体仍可视为质点，此时两个物体之间的万有引力为，根据上述条件可以计算
A．两物体的质量 B．万有引力常量
C．两物体之间的距离 D．条件不足，无法计算上述中的任一个物理量
C
****************************************************************************************

三、万有引力与重力
(
知识点睛
)
1．重力和万有引力
重力是地面附近的物体受到地球的万有引力而产生的，那么二者是否相等呢？由于地球的自转，地面上的物体（除极点之外）在做匀速圆周运动，那么物体需要提供所需的向心力，而这个向心力由什么来提供呢？
如图所示，万有引力实际产生两个效果：一个是提供物体随地球自转所需的向心力；另一个则是产生物体的重力。重力其实只是万有引力的一个分力。
由于，随纬度的增大而减小，所以物体的重力随纬度的增大而增大，即重力加速度从赤道到两极逐渐增大。但一般很小，例如一个质量为的物体在赤道上，跟着地球一起自转，做圆周运动所需的向心力为：，地球半径约为，地球自转的周期约为，代入上式求出物体在赤道上所受到的向心力，跟物体所受的万有引力相比几乎可以忽略不计。所以高中阶段我们在一般情况下可认为重力和万有引力近似相等，即。

2． 计算重力加速度的方法
⑴ 在地球表面附近的重力加速度，在忽略地球自转的情况下，可用万有引力定律来估算。
。
即在地球表面附近，物体的重力加速度。
⑵ 计算地球上空距地面处的重力加速度。由万有引力定律可得；
又由，
联立可得：，
故。
⑶ 计算任意天体表面附近的重力加速度。由万有引力定律可得：
（为该星球的质量，为该星球的半径），
又由，
联立可得。

(
例题精讲
)
题型：重力的本质
关于重力和万有引力的关系，下列认识正确的是
A．地面附近物体所受到重力就是万有引力
B．重力是由于地面附近的物体受到地球吸引而产生的
C．在不太精确的计算中，可以认为其重力等于万有引力
D．严格说来重力并不等于万有引力，除两极处物体的重力等于万有引力外，在地球其他各处的重力都略小于万有引力
BCD


题型：重力加速度的计算
如果离地面处的重力加速度是地球表面重力加速度的，则高度是地球半径的几倍？


火星的质量和半径分别约为地球的和，地球表面的重力加速度为，则火星表面的重力加速度约为
A． B． C． D．
B


在发射卫星的开始阶段时，火箭可看作匀加速直线运动，加速度大小，在卫星封闭舱内用弹簧测力计挂着质量的物体。当卫星上升到某高度时，弹簧秤的示数为，求此时卫星离地面的高度。（地球半径为，地球表面重力加速度为）



(
1
)